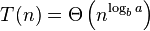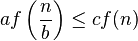算法分析---主定理

在算法分析中，主定理（英语：master theorem）提供了用渐近符号表示许多由分治法得到的递推关系式的方法。此方法经由经典算法教科书《算法导论》而为人熟知。不过，并非所有递推关系式都可应用主定理。该定理的推广形式包括Akra-Bazzi定理。
假设有递推关系式
T\left(n\right)=aT\left(\frac{n}{b}\right)+f\left(n\right)
，其中
n
为问题规模，为
a
递推的子问题数量，
\frac{n}{b}
为每个子问题的规模（假设每个子问题的规模基本一样），
f\left(n\right)
为递推以外进行的计算工作。
情形一：

 

如果存在常数\epsilon > 0，有

f(n) = O\left( n^{\log_b (a) - \epsilon} \right)，并且是多项式的小于


    那么

T(n) = \Theta\left( n^{\log_b a} \right)

情形二：

如果存在常数k ≥ 0，有

f(n) = \Theta\left( n^{\log_b a} \log^{k} n \right)

那么

T(n) = \Theta\left( n^{\log_b a} \log^{k+1} n \right)

情形三：

如果存在常数\epsilon > 0，有

f(n) = \Omega\left( n^{\log_b (a) + \epsilon} \right)，并且是多项式的大于

同时存在常数c < 1以及充分大的n，满足

a f\left( \frac{n}{b} \right) \le c f(n)

那么

T\left(n \right) = \Theta \left(f \left(n \right) \right)

 常用算法中的应用：

算法 递推关系式 运算时间 备注
折半搜索 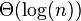T(n) = T\left(\frac{n}{2}\right) + \Theta(1) \Theta(\log(n)) 情形二（k = 0）
二叉树遍历 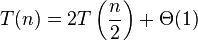T(n) = 2 T\left(\frac{n}{2}\right) + \Theta(1) \Theta(n) 情形一
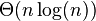归并排序 T(n) = 2 T\left(\frac{n}{2}\right) + \Theta(n) \Theta(n\log(n))
情形二（k = 0）

 







 

posted @ 2013-08-01 20:22  坚固66  阅读(1111)  评论(0)    收藏  举报