虚树 学习笔记

模板题

题目传送门
给定一棵树，每次给出 $k$ 个点，断掉一些边，然后让这些给出的点和 $1$ 号点不连通，求断边的边权和的最小值。
数据组数 $T\le 5\cdot 10^5$，树的点数 $n\le 2.5\cdot 10^5$，$\sum k \le 5 \cdot 10^5$

题目解析

我们发现每次给出的是一部分点，所以我们只需要考虑关键点，利用关键点建树跑个 DP 就好。
但是如果只考虑关键点的话，无法维护作为树的性质，所以我们还需要记录一些分叉点，就像图中一样。

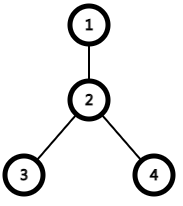
如果 $1,3,4$ 是关键点，那么为了维护树的形态 $2$ 号点就也要加进去。
换句话说，所有关键点两两的 LCA （分叉点）都要加到虚树里面。
而由关键点和分叉点构成的这棵经过“路径压缩”的树就叫虚树。

虚树的构建

显然直接 $O(n)$ 构建就不能很好利用虚树只存在较少关键点的性质，所以我们需要做到更快的构建方法。
首先我们按照所有的关键点按照 dfs 排序，然后只要取相邻两点的 LCA 即可。这样可以证明虚树的大小是 $O(k)$ 的。
我们只需要用一个栈当维护右链（也就是还未加入虚树的点）就可以建出虚树。
每次考虑一个加入的新的一个点，考虑这个点和栈顶的 LCA，记做点 $lc$。

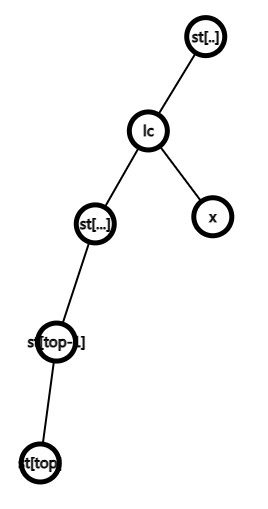
我们弹出栈里在 $lc$ 下面的点，然后将这些点的边加入虚树中。
如果 $lc$ 不在栈里面，然后让 $lc$ 入栈。
最后让 $x$ 入栈。这样复杂度就是 $O(k\log k)$ 的了，瓶颈在于排序。

清空的时候需要 dfs 一次，不然直接全清空还是 $O(n)$ 的。

#include<cmath>
#include<cstdio>
#include<iostream>
#include<algorithm>
#define db double
#define ll long long
#define Tp template<typename _T>
Tp _T mabs(_T a){ return a<0?-a:a; }
Tp _T mmax(_T a,_T b){ return a<b?b:a; }
Tp _T mmin(_T a,_T b){ return a<b?a:b; }
Tp void mswap(_T &a,_T &b){ _T t=a; a=b; b=t; return; }
struct IO{
    static const int S=1<<21;
    char buf[S],*p1,*p2;int st[105],Top;
    ~IO(){clear();}
    inline void clear(){fwrite(buf,1,Top,stdout);Top=0;}
    inline void pc(const char c){Top==S&&(clear(),0);buf[Top++]=c;}
    inline char gc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
    inline IO&operator >> (char&x){while(x=gc(),x==' '||x=='\n'||x=='\r');return *this;}
    template<typename T>inline IO&operator >> (T&x){
        x=0;bool f=0;char ch=gc();
        while(ch<'0'||ch>'9'){if(ch=='-') f^=1;ch=gc();}
        while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=gc();
        f?x=-x:0;return *this;
    }
    inline IO&operator << (const char c){pc(c);return *this;}
    template<typename T>inline IO&operator << (T x){
        if(x<0) pc('-'),x=-x;
        do{st[++st[0]]=x%10,x/=10;}while(x);
        while(st[0]) pc('0'+st[st[0]--]);return *this;
    }
}fin,fout;
#define maxn 250039
using namespace std;
int n,m,lgn,T,u,v,w;
struct Graph{
	int head[maxn],nex[maxn<<1],to[maxn<<1],c[maxn<<1],kkk;
	void _add(int x,int y,int z){ nex[++kkk]=head[x]; head[x]=kkk; to[kkk]=y; c[kkk]=z; return; }
	void add(int x,int y,int z){ _add(x,y,z); _add(y,x,z); return; }
}tr,vt;
int fa[maxn][20],minx[maxn][20],dep[maxn],dfn[maxn],d_cnt,h[maxn],st[maxn],top;
void dfs(int x,int pre){
	int i; dfn[x]=++d_cnt;
	for(i=tr.head[x];i;i=tr.nex[i]) if(tr.to[i]!=pre){
		dep[tr.to[i]]=dep[x]+1; fa[tr.to[i]][0]=x; minx[tr.to[i]][0]=tr.c[i]; dfs(tr.to[i],x);
	} return;
}
int lca(int x,int y){
	int i; if(dep[x]<dep[y]) mswap(x,y);
	for(i=lgn;i>=0;i--) if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
	for(i=lgn;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
	return x==y?x:fa[x][0];
}
void addedge(int x,int y){
	if(dep[x]<dep[y]) mswap(x,y);
	int i,sx=10000000,tx=x,ty=y;
	for(i=lgn;i>=0;i--) if(dep[fa[x][i]]>=dep[y]) sx=mmin(sx,minx[x][i]),x=fa[x][i];
	vt.add(tx,ty,sx); return;
}
int cmp(int x,int y){ return dfn[x]<dfn[y]; }
ll ans[maxn]; int flag[maxn];
void dp(int x,int pre){
	int i; ans[x]=0; //cerr<<"vis:"<<x<<" pre:"<<pre<<endl;
	for(i=vt.head[x];i;i=vt.nex[i]) if(vt.to[i]!=pre){
		dp(vt.to[i],x);
		if(!flag[vt.to[i]]) ans[x]+=mmin(ans[vt.to[i]],(ll)vt.c[i]);
		else ans[x]+=vt.c[i];
	} return;
}
void clean(int x,int pre){
	int i; for(i=vt.head[x];i;i=vt.nex[i]) if(vt.to[i]!=pre) clean(vt.to[i],x);
	vt.head[x]=0; flag[x]=0; return;
}
int main(){
	fin>>n; lgn=log2(n); int i,j,lc; for(i=1;i<n;i++){ fin>>u>>v>>w; tr.add(u,v,w); }
	dep[1]=1; dfs(1,-1);
	for(j=1;j<=lgn;j++) for(i=1;i<=n;i++)
		fa[i][j]=fa[fa[i][j-1]][j-1],minx[i][j]=mmin(minx[i][j-1],minx[fa[i][j-1]][j-1]);
	fin>>T; while(T--){
		fin>>m; for(i=1;i<=m;i++) fin>>h[i],flag[h[i]]=1; h[++m]=1,flag[1]=1;
		sort(h+1,h+m+1,cmp); st[top=1]=1;
		for(i=2;i<=m;i++){
			lc=lca(h[i],st[top]);
			while(dep[st[top]]>dep[lc]){
				if(dep[st[top-1]]<dep[lc]) addedge(st[top],lc);
				else addedge(st[top],st[top-1]); top--;
			} if(dep[st[top]]<dep[lc]) st[++top]=lc;
			st[++top]=h[i];
		}
		while(top>1) addedge(st[top],st[top-1]),top--;
		dp(1,-1); vt.kkk=0; clean(1,-1); fout<<ans[1]<<'\n';
	}
	return 0;
}