整除分块 学习笔记

板子题

板子题-UVA11526
题目大意：
给定一个 \(n\)，求 \(\sum\limits_{i-1}^{n}\lfloor \frac{n}{i} \rfloor\)。其中 \(n\) 为 \(32\) 位无符号整数。

题目解析

显然如果暴力求解肯定是不可行的，显然会 TLE，所以我们需要找一种复杂度更优的算法。
我们可以先令 \(n=10\)，观察一下函数 \(\operatorname{f}(x)=\lfloor\frac{n}{x}\rfloor\) 的图像：

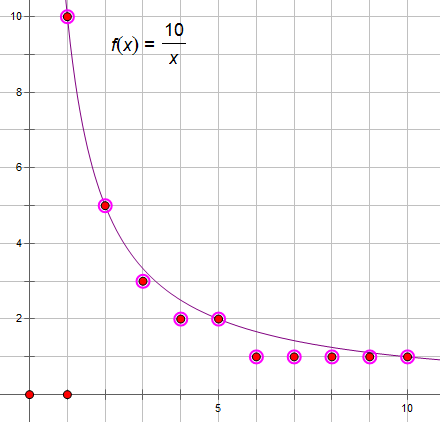
观察可以发现，不难发现：
当 \(x=1\) 的时候，\(\operatorname{f}(x)=10\)。
当 \(x=2\) 的时候，\(\operatorname{f}(x)=5\)。
当 \(x=3\) 的时候，\(\operatorname{f}(x)=3\)。
当 \(x=4,5\) 的时候，\(\operatorname{f}(x)=2\)。
当 \(x=6,7,8,9,10\) 的时候，\(\operatorname{f}(x)=1\)。
我们是否能够预处理出每个使 \(\operatorname{f}(x)\) 相同的区间来更快地计算答案呢？
不难发现以下结论：

\[\forall n\in\mathbb{N}_+, \left| \{ \left\lfloor\frac{n}{i}\right\rfloor \mid i\in\mathbb{N}_+,i\le n \} \right| \le 2 \lfloor\sqrt{n}\rfloor \]

证明：
当 \(i\le \lfloor\sqrt{n}\rfloor\) 时，\(\left\lfloor\dfrac{n}{i}\right\rfloor\) 最多 \(\lfloor\sqrt{n}\rfloor\) 个数字。
当 \(\lfloor\sqrt{n}\rfloor<i\le n\) 时，\(1\le\left\lfloor\dfrac{n}{i}\right\rfloor\le\lfloor\sqrt{n}\rfloor\)，最多有 \(\lfloor\sqrt{n}\rfloor\) 个数字。
因此最多只有 \(2\lfloor\sqrt{n}\rfloor\) 个数字。

整除分块结论

对于一个数字 \(n\)，如果 \(\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{j}\right\rfloor\) 成立，那么满足 \(i<j\le n\) 最大的 \(j\) 为 \(\left\lfloor\dfrac{n}{\left\lfloor\dfrac{n}{i}\right\rfloor}\right\rfloor\)
根据前面的结论，这种做法的复杂度为 \(\Theta\left(\sqrt{n}\right)\)。
代码：

#include<cstdio>
#define ll long long
using namespace std;
ll n,ans;
void work(){
	scanf("%lld",&n); ans=0; ll l=1,r;
	while(l<=n){ r=n/(n/l); ans+=(r-l+1)*(n/l); l=r+1; }
	printf("%lld",ans),putchar('\n'); return;
}
int main(){
	int T; scanf("%d",&T); while(T--) work(); return 0;
}

引申

显然在一般的求值题目中的式子不会这么简单，一般都形如

\[\sum_{i=1}^{n}\operatorname{f}(i)\lfloor\frac{n}{i}\rfloor \]

此时预处理出 \(\operatorname{f}(x)\) 的前缀和 \(\operatorname{g}(x)\) 就可以在 \(\Theta\left(\sqrt{n}\right)\) 求出这个式子的值了。
代码大致如下：

l=1,sum=0;
while(l<=n){
  r=n/(n/l);
  ans+=(g(r)-g(l-1))*(n/l);
  l=r+1;
}

多维数论分块

如果求值的函数中含有 \(\lfloor\frac{a_1}{i}\rfloor+\lfloor\frac{a_2}{i}\rfloor+\dots+\lfloor\frac{a_n}{i}\rfloor\)，
那么我们只需要将前面的结论的 \(\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\) 改为 \(\min \limits^{n}_{j=1} \lfloor\frac{a_j}{\lfloor\frac{a_j}{i}\rfloor}\rfloor\) 即可。
（当然 \(n=2,n=3\) 的情况比较常见）