Dinic 学习笔记
前置知识
板子题
题目传送门
我们有一张图，图中有 \(n\) 个点 \(m\) 条边，要求从源点流向汇点的最大流量（可以有很多条路到达汇点），其实就是的最大流问题。
题目解析
首先我们想到，我们可以直接dfs，然后用掉这条路径上能用的最大的流量。
不难发现这种算法是错误的，接下来我们举一个反例：
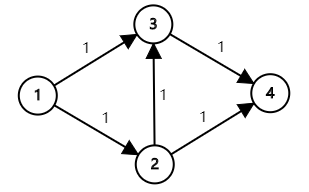
如果运气不好我们就可能走 \(1\to2\to3\to4\) ，答案是 \(1\) 。
但是我们发现正确答案是 \(1\to2\to4\) 和 \(1\to3\to4\) ，答案是 \(2\) 。
增广路
所以说我们需要采用一种反悔的方法，其实就是增广路。
增广路就是在我们用了一条边的流量之后，建一条反向边，边的流量大小就是减少的流量的大小。
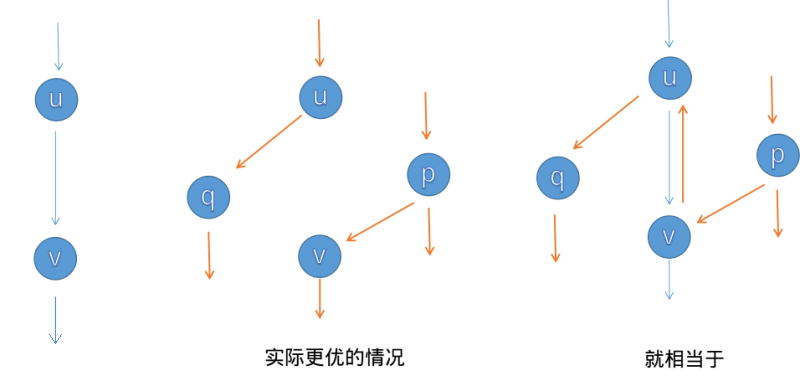
但是为什么这样是正确的呢？
略证如下图：（转自OI Wiki）
EK
那么我们就可以直接通过bfs找增广路来做了。这种做法叫做EK，代码因为太难写我就不写了吧
以下代码和Tips来自OI Wiki
Tips
#define maxn 250
#define INF 0x3f3f3f3f
struct Edge {
int from, to, cap, flow;
Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};
struct EK {
int n, m; // n：点数，m：边数
vector<Edge> edges; // edges：所有边的集合
vector<int> G[maxn]; // G：点 x -> x 的所有边在 edges 中的下标
int a[maxn], p[maxn]; // a：点 x -> BFS 过程中最近接近点 x 的边给它的最大流
// p：点 x -> BFS 过程中最近接近点 x 的边
void init(int n) {
for (int i = 0; i < n; i++) G[i].clear();
edges.clear();
}
void AddEdge(int from, int to, int cap) {
edges.push_back(Edge(from, to, cap, 0));
edges.push_back(Edge(to, from, 0, 0));
m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
int Maxflow(int s, int t) {
int flow = 0;
for (;;) {
memset(a, 0, sizeof(a));
queue<int> Q;
Q.push(s);
a[s] = INF;
while (!Q.empty()) {
int x = Q.front();
Q.pop();
for (int i = 0; i < G[x].size(); i++) { // 遍历以 x 作为起点的边
Edge& e = edges[G[x][i]];
if (!a[e.to] && e.cap > e.flow) {
p[e.to] = G[x][i]; // G[x][i] 是最近接近点 e.to 的边
a[e.to] =
min(a[x], e.cap - e.flow); // 最近接近点 e.to 的边赋给它的流
Q.push(e.to);
}
}
if (a[t]) break; // 如果汇点接受到了流，就退出 BFS
}
if (!a[t])
break; // 如果汇点没有接受到流，说明源点和汇点不在同一个连通分量上
for (int u = t; u != s;
u = edges[p[u]].from) { // 通过 u 追寻 BFS 过程中 s -> t 的路径
edges[p[u]].flow += a[t]; // 增加路径上边的 flow 值
edges[p[u] ^ 1].flow -= a[t]; // 减小反向路径的 flow 值
}
flow += a[t];
}
return flow;
}
};
它的算法复杂度为 \(O\left(nm^2\right)\) ，显然有很大的提升空间。
Dinic
这样我们来到了Dinic，阅读以下内容请确保你理解了增广路，其实上面EK和EK的代码是为了让你更好理解增广路。
Dinic的算法流程如下：
在每次增广前，通过bfs将图分层，设源点的层数为 \(1\) ，那么一个点的层数便是它离源点的最近距离。
这样我们就可以做以下两件事情：
- 如果不存在到汇点的增广路（即汇点的层数不存在），我们即可停止增广。
- 确保我们找到的增广路是最短的。
接下来是dfs找增广路的过程。
我们每次找增广路的时候，都只找比当前点层数多 \(1\) 的点进行增广（这样就可以确保我们找到的增广路是最短的）。
Dinic算法有两个优化：
- 多路增广：每次找到一条增广路的时候，我们可以利用残余部分流量，再找出一条增广路。这样就可以在一次dfs中找出多条增广路。
- 当前弧优化：一条边在一次找增广路中最多被增广一次，因为被增广一次之后就没有流量再次增广了。
时间复杂度： \(O\left(n^2m\right)\)
证明
略证：汇点的层数一开始最小是 \(1\) ，每次增广最少增加 \(1\) 层，总共有 \(n\) 个节点，所以我们最多增广 \(n\) 次。每次增广显然最坏复杂度为 \(O\left(nm\right)\) 。
Dinic的时间复杂度在稀疏图上和EK相当，但是在稠密图上远远胜过EK。
当然，我们很难让Dinic达到最坏复杂度，我们需要特殊构造数据，当然我不会构造。
Update on 2021.8.17
更改了代码，（原来写假了）。
更改的地方：在 dfs 函数增加了 if(!sum) break; 这句话。
代码
（可以过模板题）
Tips：注意开long long
#include<queue>
#include<cstdio>
#include<cstring>
#define maxn 239
#define maxm 10039
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
//#define debug
typedef int Type;
typedef long long ll;
inline Type read(){
Type sum=0;
int flag=0;
char c=getchar();
while((c<'0'||c>'9')&&c!='-') c=getchar();
if(c=='-') c=getchar(),flag=1;
while('0'<=c&&c<='9'){
sum=(sum<<1)+(sum<<3)+(c^48);
c=getchar();
}
if(flag) return -sum;
return sum;
}
int n,m,s,t,u,v,w;
int head[maxn],to[maxm],nex[maxm],kkk=1,now[maxn];
ll c[maxm];
#define add(x,y,z) to[++kkk]=y;\
nex[kkk]=head[x];\
now[x]=head[x]=kkk;\
c[kkk]=z;
int dep[maxn];
queue<int> q,E;
int bfs(){
memset(dep,0,sizeof(dep));
for(int i=1;i<=n;i++) now[i]=head[i];
q=E; q.push(s); dep[s]=1;
while(!q.empty()){
int cur=q.front(); q.pop();
for(int i=head[cur];i;i=nex[i])
if(!dep[to[i]]&&c[i]>0){
dep[to[i]]=dep[cur]+1;
if(to[i]==t)
return 1;
q.push(to[i]);
}
}
return 0;
}
ll dfs(int x,ll sum){
if(x==t) return sum;
ll res=0,tmp;
for(int i=now[x];i&&sum>0;i=nex[i]){
now[x]=i;
if(dep[x]+1==dep[to[i]]&&c[i]>0){
tmp=dfs( to[i],min(c[i],sum) );
if(tmp==0) dep[to[i]]=0;
c[i]-=tmp; c[i^1]+=tmp; sum-=tmp; res+=tmp;
}
if(!sum) break;
}
return res;
}
ll ans=0;
int main(){
//freopen("P3376_2.in","r",stdin);
//freopen(".out","w",stdout);
n=read(); m=read(); s=read(); t=read();
for(int i=1;i<=m;i++){
u=read(); v=read(); w=read();
add(u,v,w); add(v,u,0);
}
while(bfs()) ans+=dfs(s,0x7fffffffffffffff);
printf("%lld",ans);
return 0;
}
