训练记录PART4 2018.4.26~6.13
友情提醒:大部分题选自opentrains,以后有训练需要的同学慎重查看。
4.26
CF #476 E
题意:给你N(\(\leq 10^5\))个两两不同字符串,总长\(\leq 10^5\)。对于每一个字符串要保留一个非空前缀,使得得到的字符串依旧两两不同。求最终字符串总长最小可以是多少。
题解:看上去很经典的样子?开始先头脑风暴了一个傻逼贪心:按长度递增排序,每次贪心地把当前串取极短的前缀。果不其然地WA了。
考虑转化模型。如果建出了AC自动机,问题就转化成了:某些点上有关键点;现在可以把一个关键点移动到它的某个空祖先;求最终所有点深度和的最小值。无脑上了一个启发式合并套贪心:如果当前节点为空,直接挑深度最大的那个移动上来。或许有线性做法吧。
CF #475 D
题意:给你一个长度为\(N\)的字符串\(S\)。有\(Q\)个询问,每次给出\((str,k)\),要寻找一个\(S\)的子串\(S'\),使得\(str\)在\(S'\)里至少出现了\(k\)次。求\(S'\)的最小可能长度。保证每个询问的\(str\)是不同的。\(N,Q,\sum len_{str} \leq 10^5\)
题解:可以直接SAM草过去。
考虑一下分块。显然,如果一个询问比较长,我们就可以暴力\(O(N)\)扫整个串,这样怎么做都行;最经济的是直接套一个KMP,常数很小。
考虑短串怎么做。有一个经典的做法:每次枚举一种询问串的长度,然后把S中的每一个这样的位置hash,显然hash一样要并在一起。注意,此题保证询问的\(str\)互不相同,所以对于一个询问的这个hash值,我们是可以暴力扫描它所有hash与它相等的位置的。这样直接for一下就可以求出编号差为k的两个点的距离的最小值。
4.27 Petrozavodsk Winter 2018 - Carnegie Mellon U Contest
D
题意:定义一张无限分形图每条边的颜色:①一个点周围的三条边颜色分别是a,b,c。②一个环里必然是两种颜色交替。
现在给你一段由abc构成的串,问从某个起点开始依次走过这些边能否回到它自己。
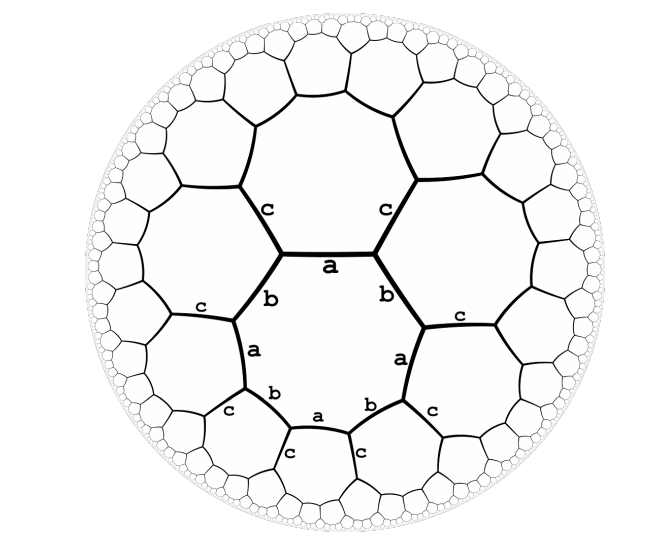
题解:感觉比较玄学。首先很显然的,每当有两个相邻字符一样时,我们一定能把它们同时消掉;如果有一段连续字符形如"ababc",我们也一定能将其换成"bab"(走环的另一侧)。画一画发现这两个消除条件是充要的……即如果原路径是闭的,我们通过反复迭代这两个操作,一定能消成空序列。
E
题意:给出一棵\(N(\leq 50000)\)的树。求有多少条简单路径,满足路径上的点标号的集合是连续的。
题解:首先套一个点分。然后从根开始算出到每个点的三元组\((max_i,min_i,len_i)\)。一条路径合法,即存在两个不同子树的点\(i\)和\(j\),满足\(max(max_i,max_j)-min(min_i,min_j)=len_i+len_j\)。分情况拆掉括号,最后转化的模型是:每一个点都有一个三元组\((x_i,y_i,z_i)\);每次询问有多少个不在当前子树里的点i,满足,\(z_i=Z\),且\((x_i,y_i)\)落在某个矩阵里。
容易想到的是,顺次枚举子树,开\(|Z|\)个容器,每个容器里在线地维护二维结构。或者说外层开一个二维结构,每个结构里维护一个哈希表(不能用set否则效率不对)。总效率即是\(O(Nlog^3N)\)的,但这样十分不好写。
能想到的最好写的做法是:首先把不同子树的限制转化成容斥,这样就可以离线了。离线后,按询问和操作的Z排序。对于相同的Z单独跑一下二维结构。这个结构具体可以用树状数组+线段树。线段树动态开点,每次做完一个Z回收一下内存。
G
题意:定义两条直线的距离为:
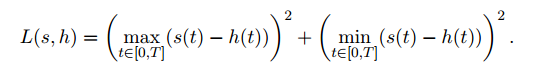
给出\(N(\leq 10^5)\)条直线。现在要求一条最优的直线\(Ax+By+C=0\),使得它与给出的每条直线的距离最大值尽量的小。
题解:显然最大和最小的差都在端点处取得。我们直接设最优直线在\(0\)处和在\(T\)处的值分别是\(X\)和\(Y\),那么它和某条直线距离就是\((X-x_c)^2+(Y-y_c)^2\)。将\((x,y)\)看成平面上的点,这个距离就变成了欧几里得距离。最后求一个最小圆覆盖即可。
H
题意:给出有重量的\(N(\leq 24)\)个物品。现在要将它们划成尽量少的组,使得每组重量\(\leq S(\leq 10^8)\)。问最小组数。
题解:比较厉害的DP含义。设\(f_S\)表示考虑完\(S\)这个集合的物品的最优状态。这个最优状态是由一个二元组\((use,rest)\)表示的,其含义是:已经用了\(use\)个背包,且最近的一个背包还剩下rest的容量(显然这个二元组满足全局偏序关系)。转移时,枚举某种状态接下来放的物品。
I
题意:有\(N(\leq 5000)\)物品,要求选最少个数的物品,恰好装满大小为\(V(\leq 5000)\)的背包。有如下几个独立子问题:(1)中位数(定义为\(\lfloor \frac{num+1}{2} \rfloor\))最小的解是什么。(2)众数出现次数最小的解是什么。(3)最大值减最小值的差最小的解是什么。
题解:
(1)有一种显然的二分做法:二分一个中位数,划成的两个物品集分别做一遍DP,枚举它们最后的重量分配合成一下即可。
但其实可以\(O(N^2)\)。一开始对物品大小排序,每次枚举其中某个物品是中位数。这样我们就知道了左右要选的物品个数(因为总的选的个数我们之前先做一遍DP可以算出来)。枚举左右两侧物品集的重量分配合一下即可。
(2)从小到大枚举众数出现次数,每次加入一些新物品,并check一下当前解是否等于最优解。
(3)比较容易想到的做法是:暴力枚举区间左端点,右侧一直线性向右移动。用双栈的方法维护这个背包。
其实还有一个做法。设\(f_{i,j}\)表示考虑了前\(i\)个物品,凑成了重量为\(j\)时的最优状态。这里状态也是一个二元组\((num,max_{min})\),表示已经选了\(num\)个点,且重量最小的点最大是多少。容易证明这也是一个偏序关系。然后我们枚举最大物品是什么,看看它之前的DP数组能否凑到num等于总num的,能的话用现在的物品质量减去上一个状态的\(max_{min}\)更新答案。
4.28 XIII Open Grodno SU Championship
L
题意:给定一个\(N\)个点的凸包。有\(M\)个询问,每次给出一条与凸包严格有交的直线。问直线到凸包各顶点的最小距离。
题解:学到了一种经典姿势:对于一条直线,我们希望把凸包划成两个凸壳,使得每个凸壳上点到直线的距离是单峰的。
先以最下面的点为原点,对凸包的边向量进行极角排序。然后每次拿直线对应的两个向量(方向相反)在有序的边向量里二分,分别找到最靠前的>它们极角的边。那么这两条边的起点即为我们要求的两个划分点。
原题直接三分即可。用这种方法,自然也能求出直线与凸包的交点。
5.5 Petrozavodsk Winter 2013 - Andrew Stankevich Contest 43
G
题意:给出一种电路串联和并联的方式。每次给出两个电路,用他们构成一个新电路。将最后的n号电路放在平面坐标系的整点上,且边不能“转弯”。
5.7 XVIII Open Cup - Grand Prix of Siberia
B
题意:边长为\(N(\leq 100)\)的正方体有\(6*N^2\)个小面,某处有宝藏。初始时,机器人在一个小面上,且有一个朝向。每次可以给它三种指令:向左转90°;向右转90°;前进一格。如果是指令3,会返回它离宝藏的欧几里得距离是是变近了还是变远了还是不变。要在\(100N\)步指令内,让机器人走到最终宝藏的位置。注意机器人和宝藏位置都是任意的,且\(N\)未知。
题解:以宝藏所在平面水平和竖直地画两条线,在立方体上延展成两个“框”;对于不在框上的点,往框的方向上走距离必然会变小。由以上分析我们可知,有且只有两个点,朝四周走离宝藏距离都变大。
继续分析,一个点到宝藏距离的三维坐标差的和最多只有\(3N\);而每一次缩进距离,坐标差的和至少减1。所以,如果我们从起点开始,每次贪心地往任意一个变近的地方走,一定能在\(O(N)\)步内走到宝藏O或是它的对应点O'。那么如何区别它们呢?
我们只需观察它们之间的路径的返回信息。O->O'的路径比O'->O的路径,变远的次数多\(N\)次。
D
题意:坐标系里有\(N(\leq 500)\)个整点,满足\(0 \leq x_1 \leq x_2 \leq \dots \leq x_n , y_1 \geq y_2 \geq \dots \geq y_n \geq 0\)。现在要在平面上画水平和垂直的线,使得每一个点都和\((0,0)\)连通,且都存在一条到\((0,0)\)的路径,使路径长度等于\(x_i+y_i\)。求所画的线的最小总长度。
题解:好像做麻烦了。首先,最上面(\(x_1\))和最右边(\(x_n\))的点必然要连过去。改一下坐标轴的位置,问题就转化为:每一个点必须能“不绕路”地走到X轴或者Y轴,求划线的最小长度。
设\(f_{i,j}\)表示在以点\(i\)确定的\(X\)轴,点\(j\)确定的\(Y\)轴中,\(i+1\)~\(j-1\)这些点的最少建路总长。决策时,枚举最靠下的、向左一直划到Y轴的点\(k\)。那么,问题将被划分为\(f_{i,k}\)和\(f{k+1,j}\)。如果不存在这样的\(k\),那点\(i+1\)必须要向下画一条竖线,然后由\(f_{i+1,j}\)转移过来。
5.9 Moscow Pre-Finals Workshop 2016 - Kent Nikaido Contest 1
B
题意:给排成一排的\(N(\leq 10^6)\)个球染上\(K(\leq 10^6)\)种颜色。再给出一个常数\(L(\leq N)\):每一次操作能选择连续的\(L\)个球,将最右边那个放到最左边。定义两种染色方案等价的,如果从某个染色方案开始,进行若干轮操作,可以得到另一种方案。问不等价的方案总数。
题解:当\(N>L\)时,一通分析可以发现,\(N\)是偶数或\(N\)是奇数且至少有种颜色涂了两次时,我们能做到交换任意两个相邻的球,那么方案数即是\(C_{N+K-1}^{K-1}\)。而\(N\)是奇数时,只需再加上每种颜色都是unique的方案数,\(C_K^N\)。
重点讨论\(N=L\)的情况,作为burnside引理的复习。此处存在\(N\)个置换,我们只需求出每一种置换的不动点个数即可。环上位移是个经典问题:假设位移了\(i\)步,一共有\(gcd(i,N)\)个等价类,方案数即为\(K^{gcd(i,N)}\)。我们外层枚举gcd值,可以知道答案为\(ans=\frac{1}{N} \sum \limits_{d|N} {K^d*\phi(\frac{N}{d})}\)。
D
题意:给出一张\(N(\leq 4*10^5)\)个点、\(M\)条边的无向图,编号为\(i\)的边的长度为\(2^i\)。现在要从1出发,走过每一条边至少一次再回到1,求走了最短长度。
题解:一开始想得复杂了。设\(c_i(\geq 1)\)表示第\(i\)条边走的次数,相当于在原图中再加入\(c_i-1\)条这样的边。那么题目要求等价于存在一条欧拉回路,即所有点的度数都需要是偶数。也就是说,对于一个点\(x\),如果它周围的边的编号为\(e_1,e_2,\dots,e_m\),那么要求\(c_{e_1} \oplus c_{e_2} \dots \oplus c_{e_m}=0\)。从这里也可以看出,\(c_i\)必然是1或者2。
现在考虑,选择把哪些边多走一次。首先构出一棵原图的最小生成树,可以证明:加的边必然在MST上(如果最优解中有一条不在MST上的边e,那么一定存在一个边的集合$ { e_1,e_2,\dots,e_m }$,使得它们达到了和e一样的效果。那么我们可以不走这条e的边,改走这个边集,答案显然更优)。而且,是否选择MST里的某条边其实已经确定了。因为我们可以从MST的叶子开始,根据叶子的度数奇偶性,来决定那条边是否选择。
5.12 XVII Open Cup - Grand Prix of Japan
5.14 Petrozavodsk Winter 2012 - Andrew Stankevich Contest 41
A
题意:将\(1\)~\(N\)填入一个\(N*N(\leq 1000)\)的幻方,要求每行、每列、每条对角线(出去后在另一侧顺延)没有重复的数字。给出一种方案或指出无解。
题解:感觉挺有趣的。打表发现,\(N \geq 5\)时,如果存在解,那么“每行由上一行循环位移2位”的构造方法一定是合法的。因此采用的做法是:每次先尝试构出一组这样的解,再check一下是否满足要求。
考虑证明这个结论的正确性(当然还是要基于,解是循环位移构造出来的)。假设每次由上一行循环位移\(g\)位:由列限制,\(gcd(g,N)=1\);由两侧对角线限制,\(gcd(g-1,N)=1 , gcd(g+1,N)=1\)。那么首先,符合要求的\(N\)是奇数。然后,因为连续三个数都要和\(N\)互质,这三个数里必然有一个是\(3\)的倍数。取\(g=2\)时,连续数位\(1,2,3\),只剩下了对\(N\)是\(3\)的倍数这个约数。即\(2\)必然是要求最宽的\(g\),结论得证。
B
题意:给出一棵\(2N(\leq 10^5)\)个点的树。现在要用至多\(N+1\)种颜色给每个点染色。每种颜色最多只能用两次,且对于任意两条边,他们两端颜色的无序对必须不等。给出一种染色方案。
题解:观察了一下过的程序,都采用了一种看起来复杂度比较高的贪心算法。我们以一个点为根搞出一个bfs序,依次决策每个点的颜色。到某点时,如果存在某种颜色一次都没用过,就优先使用它;否则在还能染一次的颜色中,暴力找到一种不冲突的颜色染上去。每次染完后,把父亲颜色和它的颜色的pair记录一下,以供后来判断颜色组是否已经被用过。做法看起来很靠谱,对于某种颜色,必然是靠的越远越好,所以优先使用没染过的颜色、采用bfs序都是有一定道理的。但是不会证明,复杂度也存疑。别的代码找不冲突颜色时,甚至是从小到大枚举的……我加了个并查集,这样每次就能\(O(1)\)定位到目前还能染一次的颜色了。
5.18 2017 Multi-University Training Contest 8
5.19 2017 Multi-University Training Contest 9
F
题意:给出\(N(\leq 10^5)\)点的有向图。再给出\(K\)个不相同的点,求它们两两最短距离的最小值。
题解:没想到这里有一个经典套路。
考虑产生最优解的那个点对\((s,t)\)。因为\(s!=t\),它们二进制表示上某一位必然不同。那么我们每次枚举两个标号不同的二进制位,把关键点分成两组,由一侧往另一侧跑最短路即可。
比赛时脑补了一个只要做一遍\(DIJ\)的做法。把每一个关键点当做起点做最短路,设\(f_i\)表示到第i个点的最短路长度,增设\(g_i\)表示在满足最短路的限制下,可以从哪些起点(关键点)转移过来。\(g_i\)是个集合,但我们只需保留它其中的任意两个元素。当我们从一个点\(x\)开始尝试更新\(y\)时,如果\(y\)是关键点,且\(g_x\)集合里不全是\(y\),那么我们用\(f_x+len_e\)来更新答案。
我们跑出的每一组解显然都是合法的;考虑最优解\((s,t)\),它一定会在t之前的那个点被统计到。
I
题意:给出三个数\(L,R,K(\leq 10^{11})\)。求\(L~R\)中最大质因子是\(K\)的数的和。
题解:显然如果\(K^2>R\),答案只可能是1或者0,那么\(K\)就被限制在一个范围内。
这是洲哥筛里的一个子问题,也是个经典的DP模型。设\(f_{i,j}\)表示如果用前\(i\)个质数去筛1~j,剩下的那些数字的和是多少。转移的话,用\(f_{i-1,j}\)来减掉第\(i\)个质数的贡献。统计第\(i\)个质数的贡献时,我们要保证它们都不是前\(i-1\)个质数的倍数,即\(f_{i-1,\lfloor \frac{j}{prime_i} \rfloor}\)(当然最后要乘上一个\(prime_i\))。记忆化一下,暴力DP即可。
5.21 Moscow Pre-Finals Workshop 2016 - Japanese School OI Team Selection
5.23 Petrozavodsk Winter 2011 - Moscow IPT Contest
B
题意:有多少个由\([1..N]\)到\([1..N]\)的映射函数\(f\),满足\(1\)~\(k\)在同一个置换里。输出答案在p(质数)进制下最后一个非0位。$0 < k \leq n < 2^{10000} , p < 10^6 \(
题解:注意,\)m\(个点在同一个置换里的方案数是\)(m-1)!\(。
直接枚举1所在的置换的大小\)i$,所以答案是 \(\sum \limits_{i=k}^n C_{n-k}^{i-k}*(i-1)!*(n-i)!\),展开后即得\((n-k)!*\sum \limits_{i=k}^n \frac{(i-1)!}{(i-k)!}\)。给求和式里配一个\((k-1)!\),变成了组合数求和,然后可以直接转化成一个特定的组合数。最后答案是\(\frac{n!}{k}\)。因为\(n\)很大,计算\(n!\)时,我们每次可以把\(n\)按模\(P\)分组,不等于0的组快速求得,等于0的组递归成\(n/P\)的子问题。
D
题意:给出一个长度为\(N(\leq 10^5)\)字符环,要求剪出\(k\)个连续段,使得每一段的字符串都一样。问其最长可能的长度。
题解:破环成链+二分长度后,又是那个经典模型。
对每一个长度为\(k\)的段,求一个hash值,并向最靠近它的不重叠的等hash值的位置连边。由于是环上询问,对于每一个结尾,我们需要知道,它一直往前跳,在长度不超过\(N\)的情况下,最多能跳几个点。这个倍增一下即可。
K
经典的圆与三角形面积交的题。乖乖地去分类讨论了。居然能把圆割成一个多边形再做。
5.30 Petrozavodsk Summer 2016 - Moscow IPT Contest
B
题意:给出\(N(\leq 5*10^5)\)个数和\(Q(\leq 2*10^5)\)次操作。①\(l\)~\(r\)每一个数都 \(and\)上\(v\)。②\(l\)~\(r\)每一个数都 \(or\)上\(v\)。③询问\(l\)~\(r\)上的最小值。
题解:好像是吉利讲过的题?
修改操作的and和or是类似的运算,都是强制把log个子树里某些位统一,只是改成0或者1的问题。
分开考虑每一位。在线段树节点里,维护每个bit位在子树里是否完全相同。那么修改的时候,如果当前操作修改的那些位在子树里本来都一样,改完后必然也一样,我们可以立即停下来,打个标记并快速维护最小值信息;否则暴力递归下去即可。时间复杂度挺显然的,势能分析一下即可。这样应该是\(O(30NlogN )\)的。然后可以用bitset的思想,进行一些位运算的骚操作,复杂度降低成\(O(NlogN)\)。
E
题意:生成\(N(\leq 10000)\)个无限长的随机bit串。求\(\max_{1 \leq i < j \leq n} LCP(S_i,S_j)\)的期望。输出在模域P下的答案。
题解:我们设\(f_L\)表示\(LCP \leq L\) 时的概率,要求不存在相同的长度为\(L+1\)的前缀。得\(f_L=\frac{C_{2^{L+1}}^n*n!}{2^{(L+1)*n}}\)。
最后答案即为:\(\sum_{i=0}^{\infty} i*(f_{i+1}-f_i)\)。
这个级数不能直接求和。因为要保留最后的分数,加到无穷显然是不现实的,只能改变求和顺序。注意到分子里实际上是一个下降幂,根据第一类斯特林数(有符号)的定义,有\(x^{\lfloor n \rfloor}=\sum_{k=0}^n S1_{n,k}*x^k\)。直接套用,并改变求和顺序,即可将无穷级数化为类等比数列。
此题\(N=10000\),可以直接暴力分治把\(S1_{n,i}\)求出来。数据再大一点可以分治FFT。
6.1 Petrozavodsk Summer 2011 - Moscow SU Unpredictable Contest
F
题意:有\(M\)个箱子,每个箱子里有若干个物品,有参数\(A_i,B_i\)。现在要给每一个物品定一个\(0 \leq \lambda_i \leq 1\),使得每个箱子里物品 $ \lambda_i $ 的之和\(=1\),且所有物品 $ \sum_i B_i* \lambda_i \geq P $。问最大的 $ \sum_i A_i* \lambda_i $ 是多少。物品总数 \(\leq 10^5\) 。
题解:YY了一个不是很优美的做法。
先假设只有一个箱子。将物品按\(A_i+B_i\)降序排序,考虑1号物品。如果\(B_1=P\),显然全都分配给A最优;如果\(B_1>P\),那么找到最小的\(i\)使得\(B_i<P,A_i>A_1\),两者匀一匀;如果\(B_1<P\),那么找到最小的\(i\)使得\(B_i>P\),两者匀一匀。这个做法正确性显然。
多个箱子也类似。先全局将物品按\(A_i+B_i\)排序,初始时,每个箱子选最大的物品。显然,若此时\(\sum B_i=P\),我们已经得到答案。若\(\sum B_i>P\),按顺序扫描排序后的物品,若扫到\(i\)时,满足\(B_i<P,A_i>A_0\)(\(A_0\)是它的组目前选的物品的参数):首先尝试把比重全都移到\(i\),如果依旧大于\(P\),那么将该组全部比重移动到\(i\),并继续往后扫描;否则,直接按比例分配该组原来的物品和\(i\),然后结束操作。\(\sum B_i<P\)也类似。
标解的做法优美很多。类似于经典题“合金”,如果把物品表示在坐标系里,能凑出的二元组\((A,B)\)分布在凸壳一侧。而合并两个箱子,相当于是它们凸包的闵可夫斯基和。所以我们只要合成最终的大凸包,再在端点上二分\(P\)即可。显然这样可以拓展到多个\(P\)的询问。
G
题意:给出三维空间里的\(N(\leq 50)\)个点的坐标。现在随机选择一个空间向量\(V\),把所有点都投影到垂直于这个向量的平面上,计算投影点构成的凸包的面积。求期望值。
题解:我们单独考虑每一个面的贡献。假设我们把它转到三维凸包的最上面并保持水平,并设\(V\)与z正半轴的夹角为\(\phi(0 \leq \phi \leq \pi)\)。显然,我们在底面向上看,必然看不到这个面。而且一般地,若\(\phi > \frac{\pi}{2}\),这个面就没有贡献。
现在考虑这个面在\(V\)向上时的贡献。观察发现,\(V\)与x正半轴的夹角\(\theta\)是不会影响其贡献的。而当角度为\(\phi\)时,面积\(S'\)会变成原来的\(Scos_{\phi}\)。
注意到,\(\phi\)越小,可能的\(V\)出现的概率就越小,所以积分式里要加上权重。最后它的贡献是:\(S*\frac{ \int_{0}^{\frac{\pi}{2}} sin(\phi)*cos(\phi) d\phi }{ \int_{0}^{\frac{\pi}{2}} sin(\phi) d\phi }=\frac{1}{2}S\)(其中S是原来凸包的表面积)。由于另一侧看不到,答案还要额外除以2。(注意这里有一个trick,如果读入只构成了一个面,就不用额外除这个2了)
H
题意:给出一个长度为\(N\)的序列和一个常数\(K\)。问最少删除几个数,使得剩下的序列能被分解成\(K\)个严格递增的子序列。对于原序列的每一个前缀都要询问一遍(\(N,K \leq 10^5;NK \leq 10^7\))。
题解:2017CTSCD2T2弱化版。
我们称一个数列的\(K-seq\)为:用K条不相交的递增链覆盖的最大长度和。
按照题解的逻辑,首先考虑数列中的相邻的三个数\(b,c,a(a<b<c)\)。考虑交换\(a\)和\(c\)的位置,变成\(b,a,c\)。显然,后者的\(K-seq\)大于等于前者。然后一通分类讨论可以证明,其实它们是完全等价的。进一步拓展,只要每连续的三个数中,最大的数和最小的数是紧靠着的,那么它们都是可以交换的(即交换后答案不变)。
考虑在线地维护。假设之前数列是{1 2 4 6 9},现在在尾部插入一个5。
我们可以一直套用上述性质进行一系列等价变换,直到不能再变换为止:
1 2 4 6 9 5 ——> 1 2 4 6 5 9 ——> 1 2 6 4 5 9 ——> 1 6 2 4 5 9 ——> 6 1 2 4 5 9
每次这样传递数字后,我们都会得到一个分段递增的数列,元素个数单调不降。
注意到,如果我们只考虑最后一段递增的数列,这个等价于普通二分求LIS维护的数组。
而最后\(K\)段的长度和,即为\(K-seq\)的答案。
如何优化这一过程呢?每次新增一个递增数列,我们都将其排在下面新开的一排,这样就排成一个杨氏矩阵。
直接暴力维护交换即可通过此题,复杂度\(O(NKlogN)\)。
其实,不仅杨氏矩阵前\(K\)行的长度和是\(K-seq\)的答案,它的前\(K\)列也是。只是前\(K\)列的长度和是拆成递减序列的最大长度和。
在CTSC那题中,不仅要维护原序列的杨氏矩阵,还要维护一下原序列*-1的杨氏矩阵(相当于原矩阵的转置)。
这样的话,每个矩阵都只要维护前\(\sqrt N\)行即可,复杂度为\(O(N \sqrt N log N)\)。
6.3 Petrozavodsk Winter 2012 - Tokyo Kroliki Contest
B
题意:给出一张\(N \leq 10^5\)的无向图。保证对于图上四个不同的点\(A,B,C,D\),如果边\((A,B),(B,C),(C,D)\)存在,那么边\((A,C)\)和边\((B,D)\)至少有一个存在。求这张图的最大点独立集大小和方案数。
题解:首先,在每个连通块内,所有点到一个固定点O的距离不会超过2。
我们不妨称距离为\(x\)的点为“\(D_x\)点”。
性质1:若某个\(D_1\)点\(X\)和\(D_2\)点\(Y\)有边,则\(X\)与所有\(D_1\)点都有边。(考虑\(Y->X->O->?\)这条路径)
性质1推论:将\(D_1\)号点分为A,B两类,其中A类点与\(D_2\)号点有边。那么,A类点构成了一个团。
性质2:一个连通块里,度数最大的点与其它所有点都有边。
性质2证明:①若不存在A类点。O就是符合要求的点,得证。
②若存在A类点,我们只需存在证明,这其中至少存在一个点\(X\)与所有点都有边。显然,\(X\)只可能与某些\(D_2\)没边。反证法,假设\(X\)只与\(D_2\)中的\(P_1,P_2,\dots,P_m\)有边,而存在一个A类点\(Y\),使得\(Y\)与\(D_2\)中的点\(P_{m+1}\)有边。我们依次考察\(P_i,X,Y,P_{m+1}\)这条路径。一旦\(X\)和\(P_{m+1}\)有边,命题即成立,所以必须是所有的\(P_i\)和\(Y\)有边。这时候,我们发现,\(Y\)和\(P_1,P_2,\dots,P_{m+1}\)都有边!用它替换成\(X\)重复上述过程。
性质3:除非是一个团,否则一个连通块里必然不会选度数最大的点。(选了它后就不能继续选了,但其实答案必然大于1)
根据性质2和3,我们每次只需判断一个连通块是否是团。如果不是团的话,直接将度数最大的点删去,把剩下的连通块答案并起来即可。
H
题意:给出一个长度\(\leq 100\)的串S。现在要删除一个子序列T,使得剩下的字符串是一个回文串。求最小字典序T。
题解:各种贪心应该都有问题;逐位确定也挺难处理的。直接设\(F_{i,j,k}\)表示\(i\)~\(j\)这个区间,删除\(k\)个字符的情况下字典序最小的T。每次讨论区间端点处的情况转移即可。为何要设最后一维呢?因为一个区间不能仅保留最小字典序,如果某个区间的两个合法解是\(a\)和\(ab\),然后我现在要在后面删除一个\(c\),那么\(abc\)反而会比\(ac\)更优。
6.6 MIPT Training Camp 2014 - JAG Autumn 2014
C
题意:有\(N\)段连续的路。要花费1s走一段,且有\(p_i\)的概率成功通过;如果失败,会跳到上一个“存档点”。初始时0号点就是存档点,每到一个点的时候都可以花费1s的时间设存档点。问最优情况下,到达点\(N\)的期望时间。\(N \leq 10^5,p_i小数点后两位\)
题解:如果只有0号点是存档点,期望时间可以递推得到,\(f_i=\frac{f_{i-1}+1}{p_i}\)。
设\(g_i\)表示,设\(i\)已经是存档点了,到达点\(N\)的期望(即求\(g_0\))。转移的话,枚举下一个存档点\(j\),那么\(g_i=min\{ g_j+f_{i...j} \}\)
直接做是\(N^2\)的。直观地想,存档点不会间隔很久设置的,我们凭借此来优化。
我们一路都不设存档点地过去,在某一段时额外的代价是:\(\frac{f+1}{p}-f\);而如果在走这一段之前,我强制设一个存档点,则此段代价是\(1+\frac{1}{p}\)。我们想要证明,在很多时刻,后者是优于前者的。那么当\(\frac{f+1}{p}-f > 1+\frac{1}{p}\)时,解得\(f>\frac{1}{1-p}\)。先不考虑\(p=1\)的情况,由于读入只有两位小数,\(f>\frac{1}{1-0.99}=100\)时后者必然更优。而f每递推一次至少+1,所以不设存档点的极长段数不会超过100。
考虑p=1的情况,会发现,如果连续两段都是1,那么中间那个点必然不会是存档点(如果是,向左移动一格必然不劣)。那我们可以把p=1的段“缩在”一起,每次只会决策最靠前的那个点。这样最多访问200段即可(最坏情况是\(p=1\)和\(p \ne 1\)交替出现)。
6.8 Petrozavodsk Winter 2016 - Zhejiang U Contest 1
D
题意:给定长度为\(N(\leq 1000)\)的排列和初始为空的一个双端队列。顺次扫描排列里的每一个数,等概率加在队列的左边或者右边。加完后,统计队列里相邻两个数的逆序对数量T。求\(T^k\)期望。\(K(\leq 50)\)且是一个常数。
题解:直接设\(f_{i,j},g_{i,j}\)表示填了前\(i\)个数,且左/右侧是\(p_i\),右/左侧是\(p_j\)时,答案的0~K次的值。每次讨论新的数填在哪一侧,组合数转移即可。
直接做效率是\(O(N^2K^2)\)的。考虑用斯特林数来优化这个过程。
最后的答案是\(\sum {x_i}^k\)(\(x_i\)表示某一种最终态)。第二类斯特林数可以将指数转化成下降幂,即\(x^k=\sum \limits_{j=0}^k S_2(k,j)*x^{\lfloor j \rfloor}\)。注意到下降幂又可以转化成组合数,所以\(x^k=\sum \limits_{j=0}^k S_2(k,j)*j!*C_x^j\)。那么我们依然可以开长度为\(K\)的数组,第\(j\)个数表示\(\sum_i C_{x_i}^j\)。这个式子可以类似组合数的递推转移。所以复杂度变成了\(O(N^2K)\)。
E
题意:有\(N\)个点的并查集和\(M\)个操作。每次给出\((s_1,s_2,l)\),将\(s_1~s_1+l-1\)和\(s_2~s_2+l-1\)对应点一一合并。求最终有几个连通块。\(N,M \leq 2*10^5\)
题解:考虑建出一个ST表(一共有\(NlogN\)个点)。对于每一次操作,将 \(l\) 二进制分解,在ST表对应层上挂上两个起始点。
最后从浅到深访问ST表每一层。对该层上挂的一些点对,暴力用并查集并起来,同时要将这些连通信息“转导”到下一层的时候。有一种实现时,找到同层的每一个联通块,那么把块里的点的左右孩子都分别合并一下。底层做完后即是最终的状态。复杂度\(O(NlogN \alpha N)\)
6.10 Petrozavodsk Winter 2014 - Ukrainian Contest
B
题意:给出第一象限的两段折线,一条严格在另一条上方。一共有\(N(\leq 10^6)\)个点,第\(i\)个点分别是\((i,x_i),(i,y_i) x_i<y_i\)。现在要将一条无限长,宽度为W的长方形光带放在上面(可以斜着放)。要求能找到一条横坐标从1到\(N\)的折线,它同时在光带和给定两个折线的内部。求最小的合法宽度W。
题解:首先有个小结论。存在这条折线,充要于对于每一个1~N的整数横坐标,存在一个纵坐标在它们的内部。
如果光带必须横着放,那么W显然是\(max(x_i)-min(y_i)\)。(注意要和0取max)
进一步推广,如果光带与x正半轴的夹角为\(\alpha(0 \leq \alpha \leq \pi)\),y坐标会变为\(ycos(\alpha)-xsin(\alpha)\)。可以只考虑\(\alpha \leq \frac{\pi}{2})\)的部分(另一侧翻转正负性再做一遍即可)。对于max或者min的式子,都可以类似求凸包的做法,维护出\(\alpha\)在某段区间里的时候,最优的函数是哪一个。最后把max和min的区间合并,对于每一个小区间里,得到了确切的W的函数,求一个极值即可。(极值可能取在端点或者导数为0的点)
F
题意:有\(N*M\)的网格图。初始时,某些网格的一些边界处已经放置了若干火柴(两个格子的公共边共享火柴),每一处最多放一根。现在要移动尽量少的火柴,使得每一个格子四周至少有一根火柴。
题解:每一个格子四周至少要有一根,可以表示为流量。移动尽量少的火柴,可以表示为费用。
将格子黑白染色建两排点。源点到左侧,汇点到右侧连流量下界为1,费用为0的边。对于两个格子,连流量上界为1的边;如果之前已经有火柴,费用为0,否则费用为1。跑一遍上下界费用流。在满足流量限制的情况下,设费用为\(c\),而费用为0的没有流的那些边数量是\(m\)(即空闲的没有用过的火柴),则必须要满足\(c \leq w\)才有解,解就是\(c\)。
6.11 Petrozavodsk Summer 2011 - Andrew Stankevich Contest 40
6.13 Petrozavodsk Summer 2016 - Pavel Khaustov Contest 2
I
题意:\(N(\leq 2^{16})\)个人打了9场比赛。每一场比赛给出一个排列表示排名。现在要挑选其中的三场,使得满足三场相对排名都不变的无序对\((x,y)\)的对数尽量少。
题解:是一道很精妙的题。直接做的话,\(C_9^3\)枚举答案,然后就是经典的三维数点,CDQ+树状数组。当然这被卡了。
我们依然去枚举这三场比赛。考虑去算答案的补集。因为正好是3场,所以补集就是一场胜两场负的点对\((x,y)\)数量。既然这样,我们可以再\(C_3^2\)枚举其中的两场,计算一下其中的逆序的数量。这样所有的\((x,y)\)都会被正好算两次。最后取个反就是要求的答案。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号