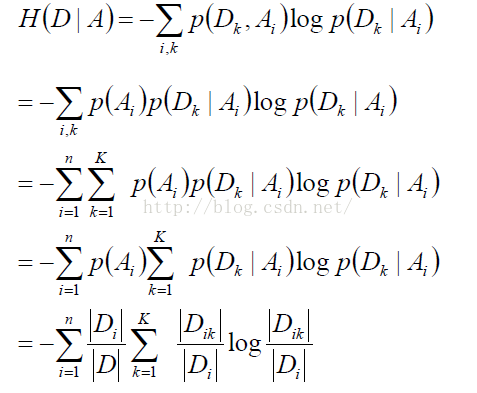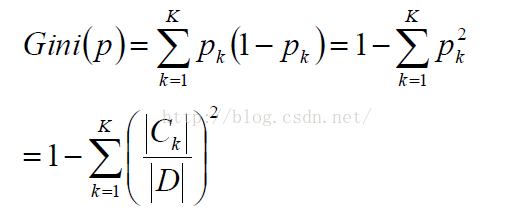关于决策树和随机森林的学习
申明:此文为学习记录过程
一:概念
决策树是一种非线性有监督分类模型,随机森林是一种非线性有监督分类模型。线性分类模型比如说逻辑回归,可能会存在不可分问题,但是非线性分类就不存在。决策树是机器学习中最接近人类思考问题的过程的一种算法,通过若干个节点,对特征进行提问并分类(可以是二分类也可以使多分类),直至最后生成叶节点(也就是只剩下一种属性)。
决策树是一种简单但是广泛使用的分类器。通过训练数据构建决策树,可以高效的对未知的数据进行分类。决策数有两大优点:1)决策树模型可以读性好,具有描述性,有助于人工分析;2)效率高,决策树只需要一次构建,反复使用,每一次预测的最大计算次数不超过决策树的深度。
信息熵:熵代表信息的不确定性,信息的不确定性越大,熵越大;比如“明天太阳从东方升起”这一句话代表的信息我们可以认为为0;因为太阳从东方升起是个特定的规律,我们可以把这个事件的信息熵约等于0;说白了,信息熵和事件发生的概率成反比:数学上把信息熵定义如下:H(X)=H(P1,P2,…,Pn)=-∑P(xi)logP(xi)
互信息:指的是两个随机变量之间的关联程度,即给定一个随机变量后,另一个随机变量不确定性的削弱程度,因而互信息取值最小为0,意味着给定一个随机变量对确定一另一个随机变量没有关系,最大取值为随机变量的熵,意味着给定一个随机变量,能完全消除另一个随机变量的不确定性
二、决策树3种算法
1.信息增益:ID3
定义为:对于特征A的信息增益为:g(D,A)=H(D)-H(D|A),信息增益就是给定训练集D时,特征A和训练集D的互信息I(D,A).选取信息增益最大的特征作为分支的节点.(后面有举例)
其中,条件熵H(D|A)的计算公式如下:
信息增益的缺点:对数目较多的属性有偏好,且生成额决策树层次多,深度浅,为改善这些问题,提出方法二.
2.信息增益率:C4.5
其等于信息增益/属性A的熵
信息增益率的缺点:对数目较少的属性有偏好,后又有方法三.
3.CART基尼指数:
其计算公式如下:
Gini系数可以理解为y=-lnx在x=1处的一阶展开.
总结之,一个属性的信息增益(率)/gini指数越大,表明属性对样本的熵较少的程度越大,那么这个属性使得样本从不确定性变为确定性的能力越强,分支时选择该属性作为判断模块使得决策树生成的越快.
三、举例
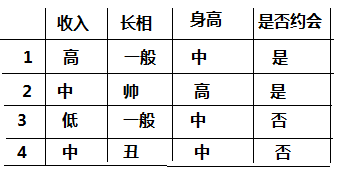
看了一遍概念后,我们先从一个简单的案例开始,如下图我们样本:
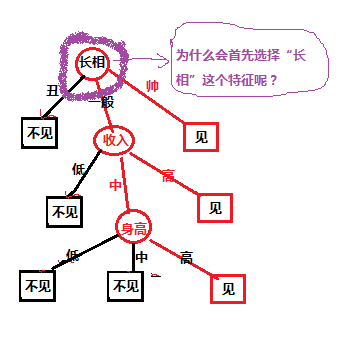
对于上面的样本数据,根据不同特征值我们最后是选择是否约会,我们先自定义的一个决策树,决策树如下图所示:
对于上图中的决策树,有个疑问,就是为什么第一个选择是“长相”这个特征,我选择“收入”特征作为第一分类的标准可以嘛?
现在我们就把信息熵运用到决策树特征选择上,对于选择哪个特征我们按照这个规则进行“哪个特征能使信息的确定性最大我们就选择哪个特征”;比如上图的案例中;
第一步:假设约会去或不去的的事件为Y,其信息熵为H(Y);
第二步:假设给定特征的条件下,其条件信息熵分别为H(Y|长相),H(Y|收入),H(Y|身高)
第三步:分别计算信息增益(互信息):G(Y,长相) = I(Y,长相) = H(Y)-H(Y|长相) 、G(Y,) = I(Y,长相) = H(Y)-H(Y|长相)等
第四部:选择信息增益最大的特征作为分类特征;因为增益信息大的特征意味着给定这个特征,能很大的消除去约会还是不约会的不确定性;
第五步:迭代选择特征即可;
按以上就解决了决策树的分类特征选择问题,上面的这种方法就是ID3方法,当然还是别的方法如 C4.5;等;
四、决策树剪枝
1. 完整树的问题
决策树对训练样本具有很好的分类能力。而一棵对样本完全分类的决策树(完整树),对未知的测试数据未必有很好的预测能力,泛化能力较差,容易出现过拟合现象。
完整树:决策树T的每个叶子节点的样本集合中的样本都为同一类型。
过拟合会导致构建出过于复杂的决策树,为解决这个问题,可以通过剪枝的方法来简化已生成的决策树,即将某个划分属性的节点的分支减掉,并将该节点作为一个某个决策结果的叶子节点(对应的决策结果可采用占多数的样本标记)。那怎么判断某个划分属性的节点是否需要剪枝呢?(剪枝在于减少叶子节点的数量)
2. 剪枝的算法
因而,我们需要设计一个分类误差评估函数,然后通过极小化决策树整体的损失函数实现剪枝。
设决策树 T 有 n 个叶子节点,设第t个叶子节点的样本集合Dt有Nt个样本,这些样本的标记类别不一定相同,假设样本集合Dt中的样本有k种标记类别,第i种类别的样本有Nti个。
那么,第t个叶子节点的样本集合的经验熵 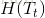
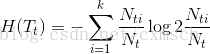
可以看出,当第t个叶子节点的样本集合只有一种标记类型时,经验熵为0。
下面给出我们的决策树 T 的损失函数的定义: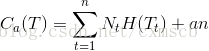
C(T)表示决策树对训练数据的预测误差,参数α控制两者之间的影响,α越大,要求模型越简单,α=0表示不考虑模型的复杂度(即可以产生较多的叶子节点)。
剪枝的过程,就是当α确定时,选择损失函数最小的模型。分类越细,叶子节点的经验熵就越小,C(T)越小,但是由于分类越细会导致叶子节点的数目会很多,α|T|(或αn)越大。损失函数反映的是两者的平衡。
决策树的生成过程只考虑了样本集合分类的纯度,只考虑更好地拟合训练数据,而剪枝过程在于减小整体的复杂度。
决策树的剪枝算法:固定某个经验值α,对划分属性的结点进行剪枝预估,若剪枝后,决策树损失函数减小了,则减掉该结点的叶节点,将该结点作为新的叶节点,该结点对应的决策结果可以为其样本集合中占多数的样本标记。(或构造不同的α值得到一些备选树,通过交叉验证的方法得到最优树)
五、决策树的过拟合解决办法
若决策树的度过深的话会出现过拟合现象,对于决策树的过拟合有二个方案:
1:剪枝
先剪枝和后剪纸(可以在构建决策树的时候通过指定深度,每个叶子的样本数来达到剪枝的作用)
引入评价函数(损失函数):所有叶节点的加权求熵,其值越小表明分类越精准,那么该决策树分类觉越好.Nt是叶节点中样本的个数.
剪枝方法之预剪枝:
从前往后生成树的过程中,从树根开始,逐一生成节点,比较其生成与不生成的C(T),在验证集上选择C(T)小的作为最终的数.
剪枝方法之后剪枝:
剪枝系数:
决策树生成后,查找剪枝系数最小的节点,视为一颗决策树,重复以上,知道只剩下一个节点,这样得到多颗决策树,在验证集上计算损失函数最小的那棵树作为最终的决策树.
2:随机森林
构建大量的决策树组成森林来防止过拟合;虽然单个树可能存在过拟合,但通过广度的增加就会消除过拟合现象
随机森林(Random forest):生成多颗决策树,投票选举的原则
引入两种方法:bootstrapping(有放回的随机抽取)和bagging(bootstrap aggragation)
bagging的方法如下:
随机森林是在bagging上做了改进,计算过程如下:
注意:随机森林或者bagging是基于若干个弱分类器组成的基本分类器进行vote决定最终的分类的,基本分类器也可以选择强分类器(如LR,SVM等),但可能因为强分类器某些特征太多明显而不能被多个分类器的平均抹掉,不能很好达到过拟合的效果.
六、决策树优缺点
优点:
->计算简单,易理解,可解释性强
->适合处理确实属性的样本,对样本的类别要求不高(可以是数值,布尔,文本等混合样本)
->能处理不相干特征
缺点:
->容易过拟合
->忽略了数据之间的相关性
->不支持在线学习,对新样本,决策树需要全部重建