BST与Treap讲解
版权声明:参考李煜东《算法竞赛进阶指南》,本文在此基础上加以改动,主要目的是帮助理解算法,我认为此书中讲的很详细,于是打算记录下来给没看过的人了解,也为以后自己复习使用。
顺便推荐一下这本书。。。
正文开始
在认识*衡树之前,我们需要先认识BST。
目录:
一.BST
1.BST的建立
2.BST的检索
3.BST的插入
4.BST求前驱/后继
5.BST的节点删除
6.BST的时间复杂度
二.Treap
三.例题
1.BZOJ3224 普通*衡树
2.BZOJ1588 [HNOI2002]营业额统计
一.BST
BST就是二叉查找树(Binary Search Tree)。
给定一棵二叉树,树上的每一个节点带有一个数值,称为节点的“关键码”。
那么一棵BST定义为:
1.该节点的关键码不小于它的左子树中任意节点的关键码
2.该节点的关键码不大于它的右子树中任意节点的关键码
满足:BST的中序遍历是一个关键码单调递增的节点序列
1.BST的建立
有时我们会遇到越界的情况,所以为了避免这种情况,我们额外建立两个节点,一个节点的关键码为正无穷,另一个节点的关键码为负无穷。
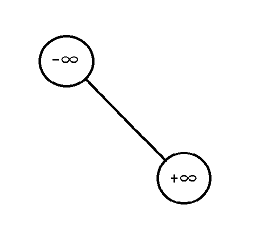
我们在开始的时候要建立由这两个节点构成的一棵BST,称为一棵“初始BST”。
例如以下就是一颗初始BST
#define N 100010//节点数 #define INF 0x7fffffff//极大值(视为正无穷) struct BST { int l,r;//左右子节点在数组中的位置 int val;//节点关键码 }a[N];//数组模拟链表 int tot,root; int New(int val)//新加节点 { a[++tot].val=val; return tot; } void Build() { New(-INF);//初始BST的初始节点 New(INF);//初始BST的初始节点 root=1;//根节点 a[1].r=2;//第一个节点的右儿子为编号为二的点,如上图 }
有关键码相同的节点同理。
2.BST的检索
在BST中查询是否存在关键码为val的节点。
设变量p等于根节点root,执行以下过程:
1.若p的关键码等于val,则已经找到。
2.若p的关键码大于val,那么有两种可能性:
(1)若p的左子节点为空,则在此BST中没有val节点。
(2)若p的左子节点不为空,就在p的左子树中递归查找。
3.若p的关键码小于val,那么也有两种可能性:
(1)若p的右子节点为空,则在此BST中没有val节点。
(2)若p的左右子节点不为空,就在p的右子树中递归查找。
例如:
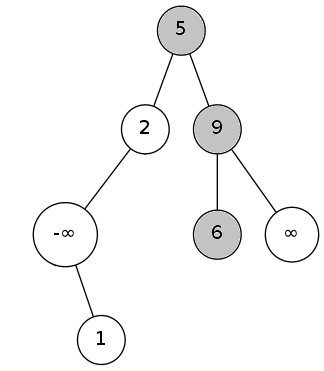
上图是查找6的过程

上图是查找3的过程,发现查找3不存在
int Get(int p,int val) { if(p==0)//不存在此节点,即搜索失败 return 0; if(val==a[p].val)//搜索成功 return p; if(val<a[p].val)//判断情况,详见上文 return Get(a[p].l,val); else return Get(a[p].r,val); }
3.BST的插入
在原BST中新加一个节点,值为val。
我们暂且认为没有关键码相同的节点,即原BST中不存在值为val的节点。
与BST的检索相同,设变量p等于根节点root,执行以下过程:
1.若p的关键码大于val,就在p的左子树中递归查找新建点的位置。
2.若p的关键码小于val,就在p的右子树中递归查找新建点的位置。
3.在发现要走向的p的子节点为空,说明val不存在时,直接建立关键码为val的新节点为p的子节点
例如:

插入3和8的过程
void Insert(int &p,int val) { if(p==0) { p=New(val);//注意p是引用,其父节点的l或r的值会被同时更新 return; } if(p<a[p].val)//与上述相同 Insert(a[p].l,val); else Insert(a[p].r,val); }
有关键码相同的节点同理。
4.BST求前驱/后继
定义:
前驱:BST中val节点的前驱定义为值小于val的前提下最大的数(关键码)
后继:BST中val节点的前驱定义为值大于val的前提下最小的数(关键码)
检索后继的过程如下:
初始化ans为具有正无穷关键码的那个节点的编号。然后,在BST中检索val。在检索的过程中,每经过一个节点,都检查该节点的关键码,判断能否更新所求的后继ans。
检索完成后,有三种可能的结果:
1.没有找到val。
此时val的后继就在已经经过的节点中,ans即为所求。
2.找到了关键码为val的节点p,但p没有右子树。
与上一种情况相同,ans即为所求。
3.找到了关键码为val的节点p,且p有右子树。
从p的右节点出发,一直向左走,就找到了val的后继。
例如:
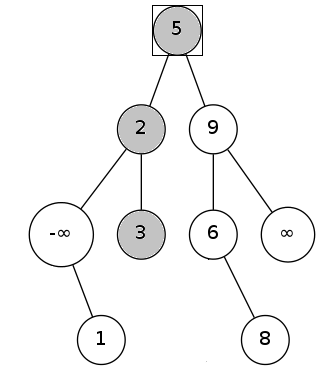
求3的后继
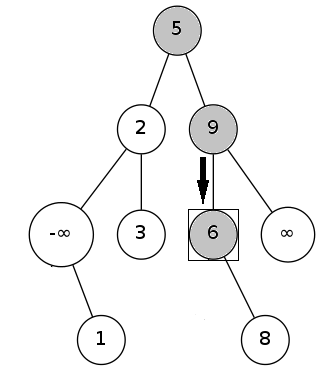
求5的后继
int GetNxt(int val) { int ans=2;//a[2].val=INF int p=root; while(p) { if(val==a[p].val)//检索成功 { if(a[p].l>0)//有右子树 { p=a[p].l; while(a[p].r>0) p=a[p].r;//从右子树上一直向左走 ans=p; } break; } if(a[p].val<val&&a[p].val>a[ans].val)//每经过一个节点,都尝试更新后继 ans=p; if(val<a[p].val) p=a[p].l; else p=a[p].r; } return ans; }
检索前驱的过程与后继相似:
int GetPre(int val) { int ans=1;//a[1].val=-INF int p=root; while(p) { if(val==a[p].val) { if(a[p].l>0) { p=a[p].l; while(a[p].r>0) p=a[p].r;//从左子树上一直向右走 ans=p; } break; } if(a[p].val<val&&a[p].val>a[ans].val) ans=p; if(val<a[p].val) p=a[p].l; else p=a[p].r; } return ans; }
5.BST的节点删除
从BST中删除关键码为val的节点。
首先,在BST中检索val,得到节点p。
若p的子节点个数小于2,则直接删除p,并令p的子节点代替p的位置,与p的父节点相连。
若p既有左子树又有右子树,则在BST中求出val的后继节点nxt。因为nxt没有左子树,所以直接删除nxt,并令nxt的右子树代替nxt的位置。最后,再让nxt节点代替p节点,删除p即可。
例如:

删除5
5的后继6代替5
6的右子树8代替6
这棵树就变成了这样:

void Remove(int val) { int &p=root;//检索节点val,得到节点p while(p) { if(a[p].val==p) break; if(val<a[p].val) p=a[p].l; else p=a[p].r; } if(p==0) return; if(a[p].l==0)//没有左子树 p=a[p].r;//右子树代替p的位置,注意p是引用 else if(a[p].r==0)//没有右子树 p=a[p].l;//左子树代替p的位置,注意p是引用 else//既有左子树又有右子树 { int nxt=a[p].r;//求后继节点 while(a[nxt].l>0) nxt=a[nxt].l; Remove(a[nxt].val);//nxt一定没有左子树,直接删除 a[nxt].l=a[p].l;//令节点nxt代替节点p的位置 a[nxt].r=a[p].r; p=nxt;//注意p是引用 } }
6.BST的时间复杂度
在随机数据中,BST一次操作的期望复杂度为O(logN)。然而,BST很容易退化,例如在BST中依次插入一个有序数列,将会得到一条链,*均每次操作的复杂度为O(N)。我们称这种左右子树大小相差很大的BST是“不*衡”的。
有很多方法可以维持BST的*衡,从而产生了各种*衡树。于是引出了下面我们介绍的入门级*衡树——Treap。
二.Treap
满足BST性质且中序遍历为相同的二叉查找树不是唯一的。这些二叉查找树是等价的,它们维护的是相同的一组数值。在这些二叉查找树上执行相同的操作,将得到相同的结果。因此,我们可以维持BST性质的基础上,通过改变二叉查找树的形态,使得树上每个节点的左右子树大小达到*衡,从而使整棵树的深度维持在O(logN)级别。
改变形态并保持BST性质的方法之一就是“旋转”。最基本的旋转操作称为“单旋转”,它又分为“左旋”和“右旋”。如下图所示。
原树:
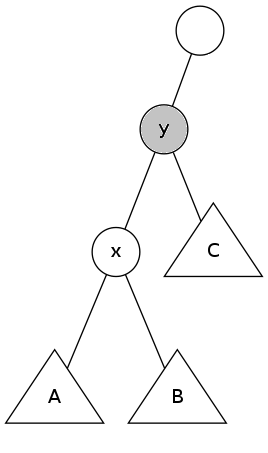
右旋zig(y):
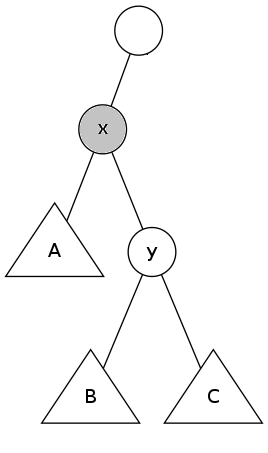
将右旋后的树再进行左旋又得到了原树
注意:某些书籍把左旋右旋定义为一个节点绕着其父节点向左或向右旋转。这里后面即将讲解的Treap代码仅记录左右子节点,没有记录父节点,为了方便起见,统一以“旋转前处于父节点位置”(旋转后处于子节点位置)的节点作为左、右旋的作用对象(函数参数)。
以右旋为例。在初始情况下,x是y的左子节点,A和B分别是x的左右子树,C是y的右子树。
“右旋”操作在保持BST性质的基础上,把x变为y的父节点。因为x的关键码小于y的关键码,所以y应该作为x的右子节点。
当x变成y的父节点后,y的左子树就空了出来,于是x原来的右子树B就恰好作为y的左子树。
右旋操作的代码如下,zig(p)可以理解为把p的左子节点绕着p向右旋转:
void zig(int &p) { int q=a[p].l; a[p].l=a[q].r; a[q].r=p; p=q;//注意是引用 }
左旋操作的代码如下,zag(p)可以理解为把p的右子节点绕着p向左旋转:
void zag(int &p) { int q=a[p].r; a[p].r=a[q].l; a[q].l=p; p=q;//注意是引用 }
合理的旋转操作可使BST变得更“*衡”。如下图所示,对其形态为一条链的BST进行一系列单旋操作后,这棵BST就变得比较*衡了。
原树:
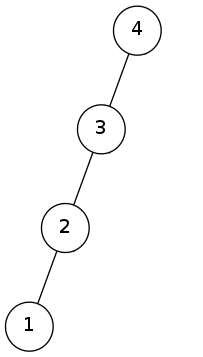
右旋zig(3):

再右旋zig(4):

现在,我们的问题是,怎样才算合理的旋转操作呢?我们发现,在随机数据下,普通的BST就是趋*于*衡的。Treap的思想就是利用随机来创造*衡条件。因为在旋转过程中必须维持BST性质,所以Treap就把随机作用在堆性质上。
Treap就是Tree+Heap。Treap在插入每个新节点时,给该节点随机生成一个额外的权值。然后像二叉堆的插入过程一样,自底向上依次检查,当某个节点不满足大根堆性质时,就执行单旋转,使该点与其父节点的关系发生对换。
特别地,对于删除操作,因为Treap支持旋转,我们可以直接找到需要删除的节点,并把它向下旋转成叶节点,最后直接删除 。这样就避免了采取类似普通BST的删除方法可能导致的节点信息更新。堆性质维护等复杂问题。
总而言之,Treap通过适当的单旋转,在维持节点关键码满足BST性质的同时,还是每个节点上随机生成的额外权值满足大根堆性质。Treap是一种*衡二叉搜索树,检查、插入、求前驱后继以及删除节点的时间复杂度都是O(logN)。
三.例题
1.BZOJ3224 普通*衡树
题目描述:
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
1. 插入x数
2. 删除x数(若有多个相同的数,因只删除一个)
3. 查询x数的排名(若有多个相同的数,因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x,且最大的数)
6. 求x的后继(后继定义为大于x,且最小的数)
题解:
Treap模版题目。
但是我们发现有可能会有重复的数字,所以我们稍加变动。
我们给每个节点增加一个域cnt,记录该节点相同的数字有多少,即该节点的“副本数”,初始值为1。
插入相同的值cnt++,减少则cnt--,直到cnt减为0时删除该点。
附上代码:
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<queue> #include<vector> #include<cstdlib> using namespace std; #define INF 0x7fffffff #define N 100010 int n,tot,root; struct Treap { int l,r; int val,len;//节点关键码、权值 int cnt,siz;//副本数、子树大小 }a[N]; int New(int x) { a[++tot].val=x; a[tot].len=rand(); a[tot].cnt=a[tot].siz=1; return tot; } void Update(int p) { a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt; } void Build() { New(-INF); New(INF); root=1; a[1].r=2; Update(root); } int GetRankByVal(int p,int k) { if(p==0) return 0; if(k==a[p].val) return a[a[p].l].siz+1; else if(k<a[p].val) return GetRankByVal(a[p].l,k); else return GetRankByVal(a[p].r,k)+a[a[p].l].siz+a[p].cnt; } int GetValByRank(int p,int rank) { if(p==0) return INF; if(a[a[p].l].siz>=rank) return GetValByRank(a[p].l,rank); else if(a[a[p].l].siz+a[p].cnt>=rank) return a[p].val; else return GetValByRank(a[p].r,rank-a[a[p].l].siz-a[p].cnt); } void zig(int &p) { int q=a[p].l; a[p].l=a[q].r; a[q].r=p; p=q; Update(a[p].r); Update(p); } void zag(int &p) { int q=a[p].r; a[p].r=a[q].l; a[q].l=p; p=q; Update(a[p].l); Update(p); } void Insert(int &p,int k) { if(p==0) { p=New(k); return; } if(k==a[p].val) { a[p].cnt++; Update(p); return; } if(k<a[p].val) { Insert(a[p].l,k); if(a[p].len<a[a[p].l].len) zig(p); } else { Insert(a[p].r,k); if(a[p].len>a[a[p].r].len) zag(p); } Update(p); } void Remove(int &p,int k) { if(p==0) return; if(k==a[p].val) { if(a[p].cnt>1)//有重复,减少副本数 { a[p].cnt--; Update(p); return; } if(a[p].l||a[p].r)//非叶子节点,向下旋转 { if(a[p].r==0||a[a[p].l].len>a[a[p].r].len) { zig(p); Remove(a[p].r,k); } else { zag(p); Remove(a[p].l,k); } Update(p); } else p=0;//叶子节点删除 return; } if(k<a[p].val) Remove(a[p].l,k); else Remove(a[p].r,k); Update(p); } int GetPre(int k) { int ans=1; int p=root; while(p) { if(k==a[p].val) { if(a[p].l>0) { p=a[p].l; while(a[p].r>0) p=a[p].r; ans=p; } break; } if(a[p].val<k&&a[p].val>a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int GetNxt(int k) { int ans=2; int p=root; while(p) { if(k==a[p].val) { if(a[p].r>0) { p=a[p].r; while(a[p].l>0) p=a[p].l; ans=p; } break; } if(a[p].val>k&&a[p].val<a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int main() { scanf("%d",&n); Build(); while(n--) { int x,k; scanf("%d%d",&k,&x); if(k==1) Insert(root,x); if(k==2) Remove(root,x); if(k==3) printf("%d\n",GetRankByVal(root,x)-1); if(k==4) printf("%d\n",GetValByRank(root,x+1)); if(k==5) printf("%d\n",GetPre(x)); if(k==6) printf("%d\n",GetNxt(x)); } return 0; }
2.BZOJ1588 [HNOI2002]营业额统计
题目描述:
营业额统计 Tiger最*被公司升任为营业部经理,他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。 Tiger拿出了公司的账本,账本上记录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节假日,大减价或者是其他情况的时候,营业额会出现一定的波动,当然一定的波动是能够接受的,但是在某些时候营业额突变得很高或是很低,这就证明公司此时的经营状况出现了问题。经济管理学上定义了一种最小波动值来衡量这种情况: 该天的最小波动值 当最小波动值越大时,就说明营业情况越不稳定。 而分析整个公司的从成立到现在营业情况是否稳定,只需要把每一天的最小波动值加起来就可以了。你的任务就是编写一个程序帮助Tiger来计算这一个值。 第一天的最小波动值为第一天的营业额
题解:
同样,我们很容易可以看出,我们只需要每次插入时求出此节点的前驱后继取min即可。
注意:此节点可能没有前驱或后继,需要特判
附上代码:
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<queue> #include<vector> #include<cstdlib> using namespace std; #define INF 0x7fffffff #define N 50001 int n,tot,root,anss; struct Treap { int l,r,cnt,len,val,siz; }a[N]; int New(int x) { a[++tot].val=x; a[tot].len=rand(); a[tot].cnt=a[tot].siz=1; return tot; } void update(int p) { a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt; } void build() { New(-INF); New(INF); root=1; a[1].r=2; update(root); } void zig(int &p) { int q=a[p].l; a[p].l=a[q].r; a[q].r=p; p=q; update(a[p].r); update(p); } void zag(int &p) { int q=a[p].r; a[p].r=a[q].l; a[q].l=p; p=q; update(a[p].l); update(p); } void Insert(int &p,int k) { if(p==0) { p=New(k); return; } if(k==a[p].val) { a[p].cnt++; update(p); return; } if(k<a[p].val) { Insert(a[p].l,k); if(a[p].len<a[a[p].l].len) zig(p); } else { Insert(a[p].r,k); if(a[p].len>a[a[p].r].len) zag(p); } update(p); } int getpre(int k) { int ans=1; int p=root; while(p) { if(k==a[p].val) { if(a[p].cnt>1) { ans=p; break; } if(a[p].l>0) { p=a[p].l; while(a[p].r>0) p=a[p].r; ans=p; } break; } if(a[p].val<k&&a[p].val>a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int getnxt(int k) { int ans=2; int p=root; while(p) { if(k==a[p].val) { if(a[p].cnt>1) { ans=p; break; } if(a[p].r>0) { p=a[p].r; while(a[p].l>0) p=a[p].l; ans=p; } break; } if(a[p].val>k&&a[p].val<a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int main() { int x; scanf("%d",&n); build(); n--;//第一个节点直接加上即可 scanf("%d",&x); Insert(root,x); anss+=x; while(n--) { scanf("%d",&x); Insert(root,x); if(getpre(x)==INF||getpre(x)==-INF) anss+=abs(x-getnxt(x)); else if(getnxt(x)==INF||getnxt(x)==-INF) anss+=abs(x-getpre(x)); else anss+=min(abs(x-getpre(x)),abs(x-getnxt(x))); } printf("%d",anss); return 0; }


