EMD学习
以下是对EMD方法的一些学习，对英文网站的翻译。
from ncl sites
EEMD，全名Extend Empirical Mode Decomposition，意为“扩展的经验模态分解”。
CEEMDAN，全名Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis，意为“利用自适应噪声分析进行的完全的集合经验模态分解”。
EMD的概述详见Lambert的网页https://www.clear.rice.edu/elec301/Projects02/empiricalMode/。
EMD是一种适用于处理非平稳非线性序列的自适应的时空分析方法。EMD进行了操作，将一个序列分成数个“模态”（IMFs, 本征模态函数）而不偏离时间域。这可以与一些时空分析方法，如傅里叶变换和小波分解，相比拟。与这些方法类似，EMD并不基于物理（原理）。相反，这些模态可能提供了在这些数据中包含了众多的信号。这个方法尤其适用于分析自然信号，而自然信号通常是非线性和非平稳的。一些典型的例子包括南方涛动指数（SOI）,NINO-3.4指数，等。
EEMD（集成的EMD）是一个辅助噪声的数据分析方法。EEMD包括筛选（sifting）出一串白噪声信号集合。EEMD不需要选择任何先验的主观标准，自然地分离，如在在原始 EMD 算法的间歇测试中。
Wu and Huang（2005）指出："白噪声强制集合在筛选过程去排除所用可能的解决方法是必要的，这从而使不同的尺度信号在由二元滤波器组描述的适当的本征模态函数（IMF）中进行整理。由于EMD是时间空间分析方法，白噪声在具有足够数量的试验的情况下被平均化。在平均过程中保留下来的唯一持久性部分是信号，然后将其视为真实且更有实际意义的答案。“此外，他们指出：”[EEMD]代表了对原始EMD的实质性改进，并且是真正的噪声辅助数据分析（NADA）方法“
CEEMDAN（利用自适应噪声分析进行的完全的集合经验模态分解）是EEMD算法的一个变体，它提供了一个精确重建原始信号和更好的IMF的谱分离的方法。
一些评论：
Salisbury and Wimbush (2002)：这种经验模式分解（EMD）方法在生成一组本征模态函数（IMF）时，提取与各种固有时间尺度相关联的能量。IMF具有良好的Hilbert变换，这可以，我们可以在时间和频率上定位任何事件。“
Lambert et al：“信号被分解的函数都在时间域中，并且与原始信号长度相同，这一事实允许保持时间变化的频率。从现实世界信号中获取IMF是很重要的，因为自然过程通常有多种原因，并且这些原因中的每一个都可能发生在特定的时间间隔内。这种类型的数据在EMD分析中很明显，但在傅里叶域或小波系数中都很隐蔽。
重要说明：Lucko et al. (2016) 提供的C代码的NCL接口。 有报告称，此代码由于使用了P. Luukko代码中的故障判据，对于某些模式会遇到模式混合问题。 NCL团队正在研究另一个版本的EEMD，看看是否可以改善这个问题。
----------------------------分割线----------------------------
Empirical Mode Decomposition
概述
EMD是一个不需要离开时间域的分解方法。它可以与其它方法（如傅里叶变换和小波分解）相比拟。这个过程对于分析自然信号（通常是非线性和非平稳的）是有用的。这部分来自我们目前知道的方法的假设（即所讨论的系统是LTI，至少是近似的）。
EMD过滤出的函数，组成了一个关于原始信号完整的，且几乎正交的基础的函数。完整性基于EMD的方法；这样分解意味着完整性。因此，这些被称为“内在模式函数”（IMF）的函数，即使它们不一定是正交的，也足以描述信号。其原因Huang et al等人在Royal Society Proceedings on Math, Physical, and Engineering Sciences中有所描述：“......这里的真正含义仅适用于局部。对于某些特殊数据，相邻的分量当然可以在不同的持续时间内具有相同频率的数据部分。但对于所有实际情况，任何两个分量在局部应该是正交的”（ 927）。
信号分解的函数都在时间域内, 并且与原始信号的长度相同, 可以保留不同频率。因为自然过程通常有多种原因，并且每种原因都可能在特定的时间间隔内发生，所以从现实世界信号中获取IMF非常重要。这种类型的数据在EMD分析中很明显，但在傅里叶域或小波系数中被完全隐藏。
一些数据非常有效地应用EMD方法，如地震读数，神经科学实验的结果，心电图（我们将在后面讨论），胃电图和海面高度（SSH）读数等。
过程
- EMD将原始信号分解成本征模态函数(IMF)分量
- 一个本征模态函数是：
1. 在过零点直接仅有一个极值
2. 均值为零为了描述这一过程,我们借用海报下面的部分:
筛选过程 - 筛选过程就是EMD用于将信号分解成IMF的过程。
筛选过程如下：
对于一个信号X(t)，从三次样条插值的局地最大值和最小值确定上下包络，让m1表示上下包络的均值。局地性是由任意参数确定；计算时间和EMD的有效性很大程度上取决于这个参数。 - 第一个分量h1计算方法如下：
h1=X(t)-m1 - 在第二个筛选过程中，h1被视作数据，m11是h1的上下包络的均值：
h11=h1-m11 - 筛选过程重复k次，知道h1k是一个本征模态函数，即：
h1(k-1)-m1k=h1k - 随后它被指定为c1=h1k，数据中第一个IMF分量，它包含了信号中最短的周期分量。我们将它从数据剩余部分中分离：X(t)-c1 = r1 这个过程重复rj次：r1-c2 = r2,....,rn-1 - cn = rn
- 结果是一组函数；在集合中函数的数目依赖与原始信号。
应用
如概述所述，EMD对于非线性，非静止信号是最有用的（正如我们稍后将看到的，或许是唯一有用的）。如这个例子所示，我们将EMD应用与几个信号中，其中两个是从网上获取的心电图原始数据。鉴于采样率并不是可用的，水平轴代表样本数量。
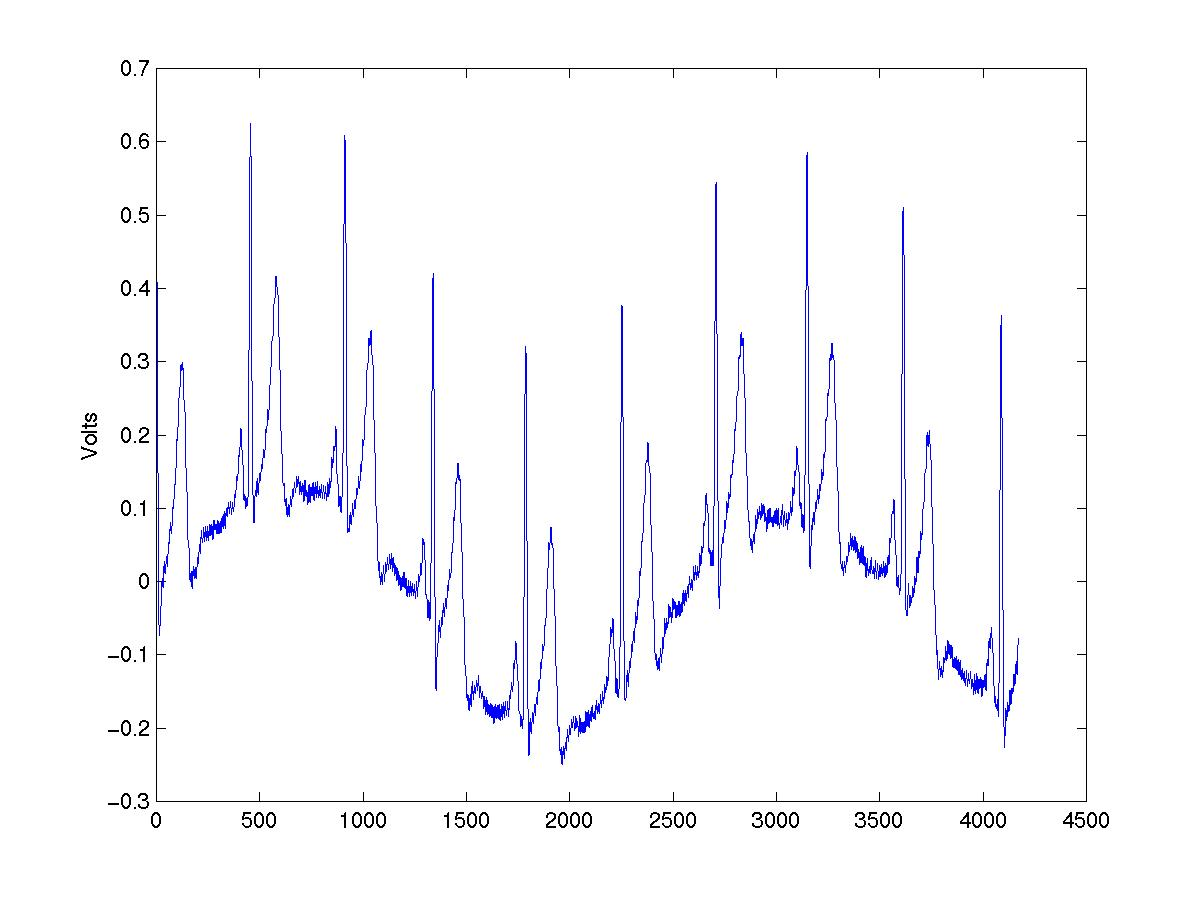ecg.mat
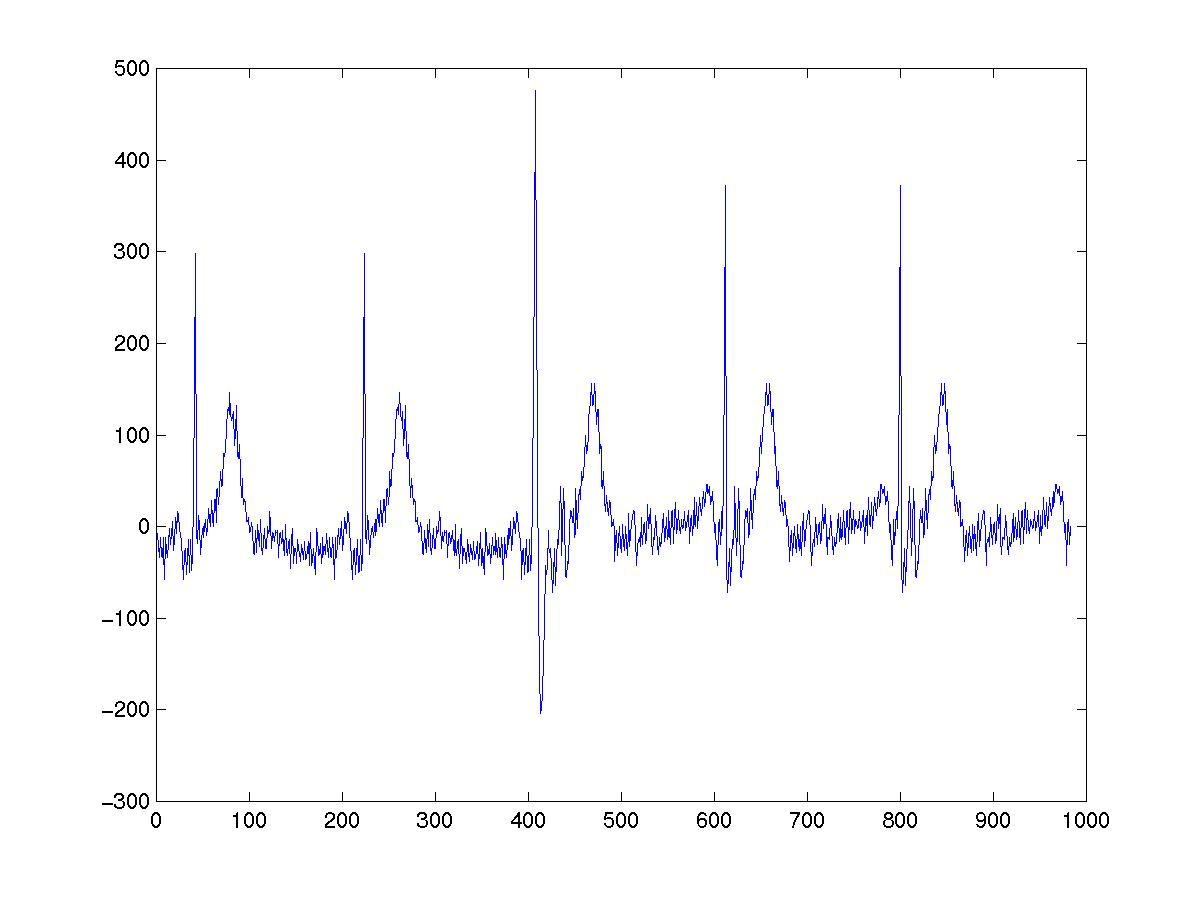ekg.mat
以下是结果EMD时每个信号；轴与原始信号图相同:
ecg.mat
图 从左上方的c14到右下方的c1。
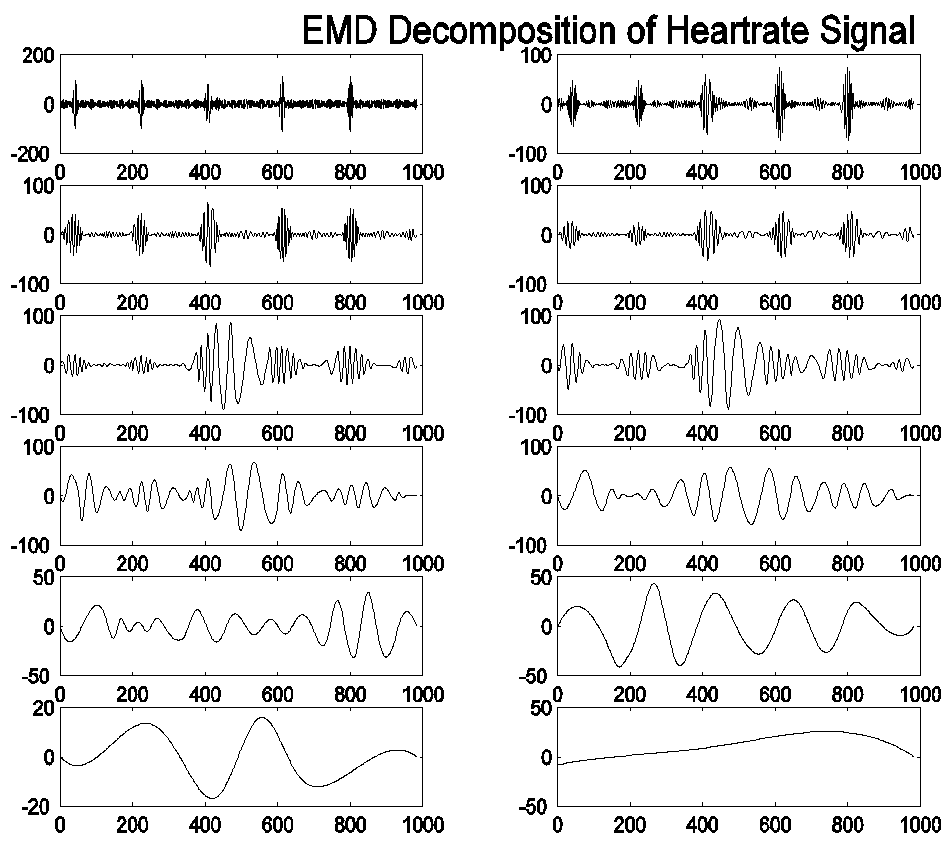ekg.mat
相反的图，从c1到c14
每个IMF代表一个不同的信号的一部分，对不同的因果关系的部分，给总复合心跳一个相当不错的分类。虽然ecg.mat中的波（我们仍然无法确定原因）导致EMD出现一些问题，但信号ekg.mat被相当有效地分解，特别是在IMF c3中，其中每个心跳被识别为一个单独的实体，在其他较小的部分中，它们共同组成一次心率。
人造vs天然
虽然遗憾的是我们没有信息的来源，但是在网络上的某个地方发现EMD已被用来相当有效地确定合成为看起来像自然数据的“假”信号和相同类型的自然信号之间的差异。
我们进行的几项实验支持这一发现。虽然有几个小组成员在网上寻找使用EMD的信号，但是一个小组成员试图从他创建的信号中获得有意义的EMD。尝试了几种不同的方法，包括使用频率随时间变化的正弦波，并添加噪声。分解结果是一团糟；我们发现我们无法用自然信号经常具有的因果模式的叠加来创建信号。
希望我们很快能够发布一些所提到的信号及它们的EMD；他们米钱迷失了，但可能还有待重新发现。
比较
EMD的重要性部分是因为他分解信号的方式比傅里叶变换强多了。由于EMD在其自己的域中保持信号的方式，它可以处理一些其它方法认为是“表现不佳”的信号。当信号进入新域时，某些选择特征随原始变量变化的方式完全丢失。虽然可以准确地检索信号，但是在没有该信息的情况下不能在新域中有效地分析信号。
EMD没有这个问题。例如，当它将时域信号分解成IMF时，每个模式功能包含有关原始信号的频率如何随时间变化的信息。因此，EMD不需要对线性或时间不变性进行最轻微的预设。这里我们提供一个例子来说明这个属性。下面是来自矢量ecg.mat的数据的傅里叶变换的一部分：
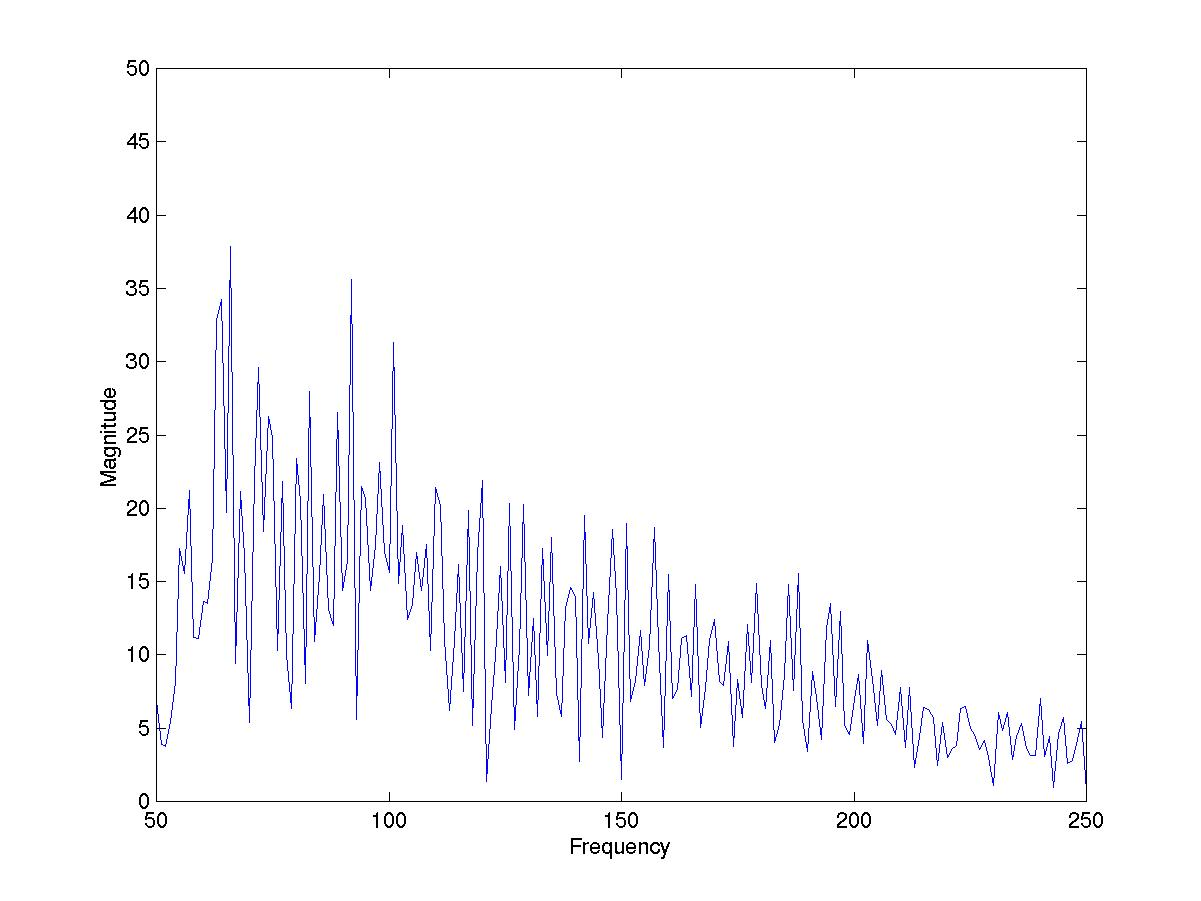
在这一领域，即使我们知道我们应该找到心跳基本在峰值(或至少是某种暗示的局部极大值)的，但我们不能找到它。我们只看到噪音。这是因为基本节拍随着时间的推移会改变其频率，以至于没有出现这种尖峰。显然，EMD在这种情况下是优越的。
结论
当用于正确的目的时，EMD显然要优越得多。对于线性的，平稳的系统的输出，EMD几乎没有价值，而且计算时间也很耗时。然而，对于非线性，非平稳信号，如现实世界中的许多信号，EMD不仅是一种有用的方法，而且可能是唯一的分析计算方法。
以我们的ECG为例，直到最近，我们使用的测试数据的读数通过眼睛检查，结果通过估计确定。这样的方法不是标准化的，也不是可重复的。EMD可以提供对自然数据的有效处理。
-----------------------------------分割线-----------------------------------
文献阅读 基于 EEMD 分解的欧洲温度序列的多尺度分析
摘要 用EEMD方法对近两百年经过均一化校正的高精度的欧洲5站逐日温度序列进行分解。
资料和方法
资料筛选：
1) 资料评估校正 通过SNHT (standard normal homogeneity test, 标准正态检验法)、BHR (Buishand range test, Buishand 范围检验法)、PET (Pettitt test, Pettitt 检验法)和VON (Von Neumann ratio test, Von Neumann 比率检验法)等方法对资料进行评估校正
2) 筛选出5个站点的资料
方法
小波分析和奇异谱分析等方法由于预先给定了基函数, 所以它们都不具备资料自适性, 并且可能会由此分解出虚假的波动尺度。
相对于这些分析方法, 经验模态分解(EMD)-集合经验模态分解(EEMD)的最大优点在于其能够以自适应方式提取信号的各分量及变化趋势。MD-EEMD 是一种适用于非线性、非平稳信号的信号分析方法, 具有可适性、正交性、后验性、完整性等特点, 在信号分析领域中有着广泛的应用。
EMD 的主要原理是将原始数据分解成有限的不同时间尺度的本征模态函数IMF, 从而得出信号在不同时间尺度上的变化情况。为使EMD 的分解结果能够更准确地揭示信号的变化特征, 就需要分解出的IMF 具有现实的物理意义。一个具有现实物理意义且可信度较高的IMF 应满足以下两点要求:
1) 在整个极值资料中, 极值的数目必须与跨零点的数目相等, 或最多只能差一个;
2) 在任何时间点上, 由极大值包络线和极小值包络线所定义的局部均值包络线的值为0。
EMD存在缺陷——边缘效应和尺度混合。尤其是尺度混合, 它不仅会造成各种尺度振动模态的混合, 甚至可以使个别IMF 失去物理意义。
因此, 在EMD 的基础上, 引入了一种利用噪音辅助的集合EMD 分解方法, 即EEMD[13]。它能更好地解决尺度混合的问题。
EEMD特点，继承了EMD 的自适性; 引入了白噪声扰动并进行集合平均，避免了尺度混合问题, 使得最终分解的IMFs 保持了物理上的唯一性。
EEMD 具体步骤：
1）将待分析的资料数据序列叠加上给定振幅的白噪声序列。
2）将加入白噪声后的数据——混合的信号(原始信号)进行EMD 分解。
3）反复重复这两步骤, 每次加入振幅相同的新生的白噪声序列从而得到不同的 IMFs。
4）最后将各次分解得到的IMFs 求集合平均, 并将其作为最终的分解结果。
这样就得到了各个固有尺度上的IMFs。此外, EMD 除了不能保证每个IMF 都具有很好的物理意义外, 亦不能估计分解得到的IMFs 的信度。但EEMD 可借助于白噪声的集合扰动进行显著性检验, 从而给出各个IMF 的信度[14−15]。
本文在对逐日温度序列进行EEMD 分解时, 用于集合分解的扰动白噪声与原始信号的信噪比(标准差比)为0.2 或0.3, 集合样本数取为100。另外,本文对EEMD 分解的IMFs 还进行了显著性检验。
通过对 5 个站点近200 年的逐日资料进行EEMD分解，可以得到14 或15 个IMFs(Cj, j = 1, 2, …,14 或15)以及残差序列。这些IMFs 依次反映了从高频到低频不同时间尺度的温度波动特征。正如所预期的, 显著性检验表明年循环在各个站点都非常显著(各个站点中抽取的14 或15 个IMFs 中, 第6～7 个分量包含年尺度信号分量)。为了更准确地分析温度的低频变化特征, 本文以年尺度分量为界将信号划分为高频分量(年及年以下尺度)和低频分量(年以上尺度)两部分, 并重构低频分量。
低频信号的重构按以下步骤进行:
1) 将集合平均得到的包含年尺度的两个分量相加(C6+C7)并进行EMD 分解, 分解后的第一个分量为年循环;
2) 将步骤1) 分解得到的第2 至14 或15 个分量叠加到EEMD 分解得到的第8 至14 或15 个分量中, 构成新的低频分量序列。然后再对重构的低频信号进行 EEMD 分解, 提取各时间尺度上的低频分量。图1 显示了Milan 站通过显著性检验的 6 个低频分量的信号。为了比较,同时给出了相应尺度上小波分解的结果。两次EEMD分解的结果非常吻合, 但与小波分解的结果在某些尺度上略有差异, 例如在C12 尺度上。值得注意的是差异最大的时段出现在边缘效应最强的两端。
结果分析
2.1 低频信号的尺度分析
上述各站点的低频信号的分解结果得到了6~8个显著性水平高的低频分量(图2), 分别代表温度变化的年际、年代际、世纪尺度的波动情况。具体时间尺度如表2 所示。为了对比分解结果, 对无缺失数据的Stockholm站和Praha-Klementinum 站年平均序列进行EEMD 分解。结果表明: Stockholm 站具有平均周期为2.7, 5.9, 16.6, 28.6, 64.1 和169.8 a 等6 个不同尺度的显著分量, Praha-Klementinum 站则有平均周期为2.6, 5.75, 12.4, 21.1, 41.3 和212 a 等6个不同尺度的显著分量。考虑到数据长度的限制以及低频信号的尺度有一定的波动范围, 用逐日资料和年平均序列的到结果有很好的一致性, 尤其是Stockholm 站。
此外, 考虑到相邻的IMFs 有可能包含部分相近尺度的信号, 因此, 为了得到个尺度更明确的IMFs, 可以将低频信号的分解结果进行再分解处理[13]。具体方法如下。
1) 将两个相邻分量相加Cj +Cj +1 进行EMD 分解(此时的合成信号对EMD 分解更加敏感), 再次分解后的第一个IMF 既为第Cj 个分量。
2) 抽取的第一个IMF 既为第j 个分量Cj (这里用Dj 表示), 再将剩余部分(Cj +Cj +1-Dj)加到第j+2个分量Cj +2 中, 分解得到Cj+1。
由于不同地区的温度低频变化的时间尺度并不唯一且有可能表现出阶段性的变化[16], 因此, 我们用各站多次分解结果的尺度范围作为欧洲温度低频波动的尺度, 并且由于多次分解的结果均在一个主要的取值范围内变化, 因此可以认为分解的尺度具有代表性。
经过多次分解后的温度波动有以下几个主要尺度范围:
1) 年际尺度存在着平均周期为3.0~3.7 和5.2~7.5 a 的波动尺度, 这与ENSO 存在着2~7 a 的波动在时间尺度上有一致性且重多研究表明ENSO 事件对全球的气候变化有影响;
2) 年代际尺度存在着平均周期为11.0~15.0, 21~28 和50~75 a的波动尺度;
3) 世纪尺度存在着平均周期为100~125 和140~156 a 的波动尺度。对于温度变化趋势的抽取, 我们将最后的1~2 个IMFs(C14 和C15)和EEMD 分解的残差趋势项(残差项与其平均值之差)整合在一起反映温度在整个时间尺度内的变化趋势。
2.2 低频信号的波动分析
虽然从平均周期上看温度波动表现出很好的离散尺度且温度的低频变化有很好的一致性, 单个分量在周期性、波动幅度上却表现出一定的差异, 如图3~5 所示。1) 非周期性及准周期性。欧洲温度波动的低频信号在平均尺度上表现出很好的一致性, 但个分量的波动变化却表现出准周期性甚至是非周期性。如Praha-Klementinum 站在时间尺度为50~75 a (C12)的年代际尺度变化中, 1850—1940 年间的周期长度明显小于1850 年前和1940 年后的周期长度, 但Milan站在该尺度的波动中却显示出准周期性特征。整体上讲, 5 个站在年代际尺度的分量上, 周期长度的变化要明显大于年际尺度和世纪尺度的变化。2) 波动幅度变化及波动的时段性。温度低频变化在波动振幅上也表现出很好的局域性特点。如年际尺度的波动上Milan 站的波动幅度明显小于Praha-Klementinum站, 而这种差异性在世纪尺度的信号分量中表现的更明显。如图5(a)所示, Bologna站的波动振幅明显小于Stockholm, Praha-Klementinum,Milan 和Wien 4 个站, 但这种差异性在年代际尺度的分量中表现不如年际尺度和世纪尺度的明显。值得注意的是在50~75 a 的年代际尺度和世纪尺度的变化中, 部分站点温度变化在1980 年以后表现出强烈的上升趋势, 如Stockholm 站。此外, 低频信号的各分量在整个数据长度的范围内表现出明显的时段性尤其是年际尺度和年代际尺度的变化,但世纪尺度波动时段性却不明显。5 个站在3.0~3.7 a(C8)和5.2~7.5 a (C9)的年际尺度上都表现出很好的时段性如图3(a)和(b)所示。年代际尺度上Stockholm,Bologna, Praha-Klementinum 和Milan 在11.0~15.0 a尺度上表现出很好的时段性, 如Praha-Klementinum在1850—1940 年间的波动幅度明显小于1850 年前和1940 年后的波动幅度。另外, Stockholm 和Praha-Klementinum 两站在50~75 a 的尺度上表现亦很明显。温度低频变化在周期性和波动振幅变化上表现出很好的局域性, 可能是由局域气候不同造成的。此外, 对于欧洲地区平均温度而言, 1900—1950 年处于平稳的上升阶段, 1950—1970 年处于较小的波动阶段, 1970 年以后则处于加速上升阶段[1]。整体而言, 趋势项显示1900 年以后5 站均呈上升趋势, 而在1980 年以后则呈现加速上升趋势, 且在整个序列长度范围内温度增幅为1.8~2.75℃, 其中以Stockholm 站表现出尤为明显。世纪尺度和50~75 a的年代际尺度均显示1970 年以后温度呈现出上升趋势。在1900—1950 年间, 世纪尺度变化呈下降趋势, 50~75 a 的年代际尺度则表现出现先升后降的波动变化。这说明趋势项对于平均温度的变化有着明显的影响。
2.3 年循环与季节变化
本文中定义的年循环为年尺度分量, 具体抽取方法如2.1 节所示: 将包含年尺度的两个分量相加(C6+C7)并进行EMD 分解, 分解后的第一个分量为年循环。季节变化用年、年以上尺度低频分量及趋势项的整合结果来表示。就全球平均温度而言, 20世纪的增温分两个阶段发生, 即10—40 年代(增温幅度为0.35℃)和增温更强的70 年代末以后(幅度约为0.55℃)。因此, 我们将结合全球平均温度的变化分析欧洲季节变化及年循环变化, 如图6 所示。考虑到冬夏两季的温度对平均温度的影响比较大, 因此, 本文主要分析冬夏两季的季节长度和强度的变化, 如图6(a)和(b)所示。
1) Milan 站。相对于1850 年以前, Milan 站在1860 年以后表现出明显的夏季变长且高温增多, 高温最多时间段出现在1900—1910 年、1940—1955年及2005 年至今。从整个数据长度范围内看, 冬季一直在变短变弱, 尤其在1970 年以后这种变化趋势更明显。
2) Stockholm 站。在整个数据长度范围内, 1756—1860 年间夏季最长转折点出现在1860 年, 1860年以后夏季开始变短且夏季最短时间段出现在1860—1900 年间。另外一个明显的转折点出现在1970 年, 即在1970 年以后夏季开始变长但高温增多不明显。1920 年以后冬季低温明显减少, 但在1960—1970 年间低温略有增多, 1970 年以后冬季变短和低温减小的现象更加明显。相同情况也出现在Praha-Klementinum站, 两站在季节变化上有着很好的一致性。综合而言, 欧洲季节变化显示: 70 年代以后夏季变长、冬季变短、低温减少, 且有部分站点出现夏季高温增多现象。因此, 70 年代末以来的增温很可能是冬夏两季增温的同时, 夏季变长、冬季变短共同作用的结果。温度信号初次分解的显著性检验显示年循环在欧洲各站点上都表现得非常明显。传统意义上的年循环是一个气候变量的日(月)的函数, 定义为多年气候变量的平均值。因此, 传统的年循环通常是一个不随年变化的量。而事实上温度的年循环是逐年变化的, 如图6(c)和(d)所示。此外, 考虑到部分缺失的数据对结果的影响, 本文选择具有代表性的两站(Milan 站和Stockholm 站)进行着重分析。近二百多年欧洲各站的年循环变化特征有两类: 1) 年 循 环 强度逐年变化较小, 如Milan 和Bologna 两站, 其中以Milan 站为代表; 2) 年循环年强度逐年变化较大, 如Stockholm, Wien 和Praha-
Klementinum 站, 以Stockholm 站为代表。1) 在整个数据长度范围内Milan 站的年循环较弱, 年份振幅波动为±10℃, 年循环较强的年份振幅波动为±13.5℃, 且年循环最强年份出现在1850—1880 年及1940—1950 年间。1830 年以前年循环强度较大且无明显的变化, 而在1830—1850 年和1910—1940 年间出现一个相对减弱的阶段。1965年至今年循环强度明显减小且振幅波动范围处于±10~±12℃之间。2) Stockholm 站的年循环强度逐年变化很大。年循环较弱的年份振幅波动为±5℃, 而较强年份振幅波动达±15℃。从整个数据长度看, 1830 年以前年循环强度较强且无明显变化。而年循环减弱的转折点出现在1850 年, 1850 年以后年循环减弱且在1910—1940 年间和1980 年以后表现尤为明显。综合而言, 两站在1910—1940 年间及1970 年代末以来年循环强度均处于减弱状态, 且年循环减弱可能是由于平均温度的增加而造成的。
3 结果与讨论
EEMD 是一种适用于非线性、非平稳序列的信号分析方法。将EEMD 应用于气候要素时间序列,可提取可靠真实的气候变化信号。特别地, EEMD可以得到气候变化的固有时间尺度。本文对欧洲5站近200 年高精度的逐日温度序列的EEMD 分析得到以下认识。
1) 欧洲温度的低频变化存在着3 个典型的固有时间尺度, 即年际尺度、年代际尺度和世纪尺度。具体地, 年际变化存在着3.0~3.7 和5.2~7.5 a 的平均周期; 年代际变化存在着11.0~15.0, 21~28 和图 5 5 站世纪尺度的信号分量C13(100~125 a 和140~156 a)(a)和变化趋势(b)Fig. 5 Century scale C13 of five stations (100-125 a and140-156 a) (a) and trends of five stations (b)50~75 a 的平均周期; 世纪尺度存在着100~125 和140~156 a 平均周期。就平均周期而言, 欧洲温度的低频变化存在着很好的一致性。
2) 尽管欧洲温度的变化有3 个典型的时间尺度, 但另一方面, 温度变化也显示了准周期性甚至非周期性特征。特别地, 在年代际时间尺度上, 温度演变的周期长度随时间变化显著。
3) 尽管欧洲5 站温度的低频变化在各时间尺度上都显示出较好的同步性, 但温度的波动幅度却有明显的差异。
4) 就温度变化趋势而言, 1900 年以后的变暖幅度明显大于之前100 年的变化幅度。在世纪尺度的变化上, 70 年代末以来的增暖趋势非常显著, 这与全球的情形类似。
5) 年循环与平均温度的变化有较好的关联, 年循环强度在1910—1940 年及70 年代末以来的两个暖期里均处于偏弱的状态, 尤其是最近30 年里年循环强度减弱趋势更加明显。此外, 与1910—1940 时段相比, 在70 年代末以来的暖期里, 夏季更长冬季更短。这两个暖期的夏季长度的差异可能意味着: 40年代的增暖表现为冬季和夏季平均温度的都升高;但对于70 年代末以来的增暖, 夏季变长冬季变短却起了重要的作用。
