概率统计学习——（三）多维随机变量及其分布
参考自 盛骤, 谢式千, 潘承毅. 概率论与数理统计 第四版[M]// 概率论与数理统计, 第四版. 高等教育出版社, 2008.
二维随机变量
一般，设E是一个随机试验，它的样本空间是S={e}，设X=X(e)和Y=Y(e)是定义在S上的随机变量，由它们构成的一个向量(X,Y)，叫做二维随机向量或二维随机变量.
二维随机变量(X,Y)的性质不仅与X即Y有关，而且还依赖于这两个随机变量的相互关系.
定义 设(X,Y)是二维随机变量，对于任意函数x,y，二元函数：
称为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数.
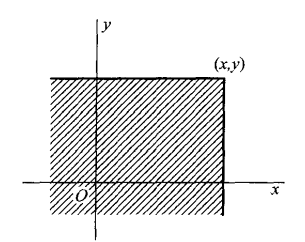
如果将二维随机变量(X,Y)看成是平面上随机点的坐标，那么，分布函数F(x,y)在点(x,y)处的函数值就是随机点(X,Y)落在如图所示的，以点(x,y)为顶点而位于该点左下方的无穷矩形域内的概率.
分布函数F(x,y)具有以下的基本性质:
1° F(x,y)是变量x和y的不减函数，即对于任意固定的y，当x2>x1时 \(F\left(x_{2}, y\right) \geqslant F\left(x_{1}, y\right)\)；对于任意固定的x，当\(y_{2}>y_{1}\)时，\(F\left(x, y_{2}\right) \geqslant F\left(x, y_{1}\right)\).
2° \(0 \leqslant F(x, y) \leqslant 1\)，且
\(\text { 对于任意固定的 } y, F(-\infty, y)=0\)
\(\text { 对于任意固定的 } x, F(x,-\infty)=0,\)
\(F(-\infty,-\infty)=0, F(\infty, \infty)=1\)
3° \(F(x+0, y)=F(x, y), F(x, y+0)=F(x, y)\)，即\(F(x, y)\)关于x右连续，关于y也右连续.
4° 对于任意\(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), x_{1}<x_{2}, y_{1}<y_{2}\)，下述不等式成立
\(F\left(x_{2}, y_{2}\right)-F\left(x_{2}, y_{1}\right)+F\left(x_{1}, y_{1}\right)-F\left(x_{1}, y_{2}\right) \geqslant 0\).
如果二维随机变量(X,Y)全部可能取到的值是有限对或可列无限多对，则称(X,Y)是离散型的随机变量.
设二维随机变量(X,Y)所有可能取的值为(xi,yi),i,j=1,2,...,记P{X=xi,Y=yi}=pij,i,j=1,2,...为二维离散型随机变量(X,Y)的分布律，或随机变量X和Y的联合分布律.
连续性的二维随机变量
概率密度
联合概率密度
n维随机向量 或 n维随机变量
边缘分布
二维随机变量(X,Y)作为一个整体，具有分布函数F(x,y). 而X和Y都是随机变量，各别也有分布函数，将它们分别记为Fx(x)，FY(y),依次称为二维随机变量（X,Y)关于X和关于Y的边缘分布函数。
posted @ 2020-09-08 20:27
