topcoder srm 595 div1 [FINISHED]

problem1 link

对于每个位置$i$,得到它最后被哪个操作所覆盖. 假设最后所有位置上的操作集合的大小为$s$,那么答案为$2^{s}$

problem2 link

假设$b$的位置固定，那么不同的$a$会使得$[a,b]$有两种情况，第一种，$[a,b]$ is nice;第二种$[a,b]$有一个后缀的连续$G$但是少于$minGreen$个。第一种情况，$[c,d]$可以任意取；第二种情况，假设$[a,b]$的后缀有$m$个‘G’，那么$[c,d]$要么is nice,要么其前缀需要有至少$minGreen-m$个连续‘G’。所以需要维护$b$之后有多少个区间is nice以及有多少区间不是nice但是有$t$个前缀‘G’的区间个数。

problem3 link

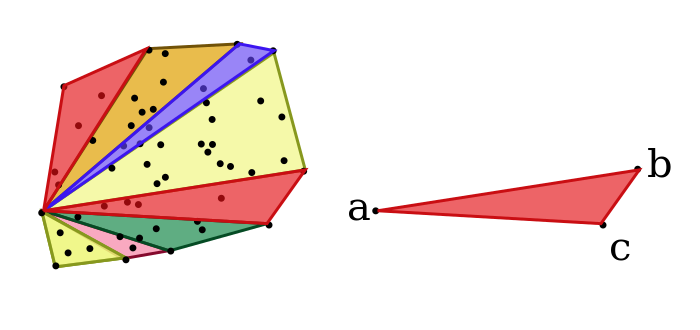
一个凸包可以划分成若干个三角形。为了计算的方便性，可以假设凸包划分三角形的方式是凸包最左下角的顶点与其他顶点连线。设$abc$是一个三角形的顶点，其中$a$是凸包左下角的顶点，那么这时候$bc$一定是凸包的一个边。所以$bc$另一测的点必然都不会出现，比$a$还左下的点也都不能出现。另外在线段$bc$上的点也都不能出现（避免重复计算）。

 

code for problem1

#include <vector>
#include <set>

class LittleElephantAndIntervalsDiv1 {
 public:
  long long getNumber(int M, const std::vector<int> &L,
                      const std::vector<int> &R) {
    std::vector<int> a(M, 0);
    int n = static_cast<int>(L.size());
    for (int i = 0; i < n; ++i) {
      int left = L[i] - 1;
      int right = R[i];
      for (int j = left; j < right; ++j) {
        a[j] = i + 1;
      }
    }
    std::set<int> b;
    for (int i = 0; i < M; ++i) {
      if (a[i] != 0) {
        b.insert(a[i]);
      }
    }
    return 1ll << b.size();
  }
};

code for problem2

#include <algorithm>
#include <string>
#include <vector>

class LittleElephantAndRGB {
 public:
  long long getNumber(const std::vector<std::string> &list, int m) {
    std::string S;
    for (const auto &s : list) {
      S += s;
    }
    int n = static_cast<int>(S.size());
    std::reverse(S.begin(), S.end());
    auto g = Compute(S, m);
    std::reverse(S.begin(), S.end());
    auto f = Compute(S, m);
    long long result = 0;
    std::vector<int> sum(m, 0);
    long long num = 0;
    for (int c = n - 1; c > 0; --c) {
      {
        int idx = n - 1 - c;
        int p = g[idx].first;
        num += g[idx].second;
        int start = p >= m ? 1 : (idx - p + 1) - g[idx].second + 1;

        for (int j = std::min(p, m - 1); j >= 1; --j, ++start) {
          sum[j] += start;
        }
      }
      result +=
          static_cast<long long>(f[c - 1].second) * (n - c + 1) * (n - c) / 2;
      result += num * (c - f[c - 1].second);
      if (m > 1) {
        for (int j = 1; j < m && j <= f[c - 1].first; ++j) {
          if (j < f[c - 1].first) {
            result += sum[m - j];
          } else {
            result += sum[m - j] *
                      ((c - 1 - f[c - 1].first + 1) - f[c - 1].second + 1);
          }
        }
      }
    }
    return result;
  }

 private:
  std::vector<std::pair<int, int>> Compute(const std::string &s, int m) {
    int n = static_cast<int>(s.size());
    std::vector<std::pair<int, int>> f(n);
    f[0].first = s[0] == 'G' ? 1 : 0;
    f[0].second = s[0] == 'G' && m == 1 ? 1 : 0;
    for (int i = 1; i < n; ++i) {
      f[i].first = s[i] == 'G' ? 1 + f[i - 1].first : 0;
      f[i].second = 0;
      for (int j = i, c = 0; j >= 0; --j) {
        c = s[j] == 'G' ? (c + 1) : 0;
        if (c >= m) {
          f[i].second = j + 1;
          break;
        }
      }
    }
    return f;
  }
};

code for problem3

#include <algorithm>
#include <vector>

class Constellation {
 public:
  double expectation(const std::vector<int> &x, const std::vector<int> &y,
                     const std::vector<int> &prob) {
    const int n = static_cast<int>(x.size());
    std::vector<std::vector<std::vector<int>>> area(
        n, std::vector<std::vector<int>>(n, std::vector<int>(n, 0)));
    std::vector<int> sort_idx(n);
    for (int i = 0; i < n; ++i) {
      sort_idx[i] = i;
    }
    std::sort(sort_idx.begin(), sort_idx.end(), [&](int l, int r) {
      return x[l] < x[r] || (x[l] == x[r] && y[l] < y[r]);
    });
    for (int i = 0; i < n; ++i) {
      for (int j = 0; j < n; ++j) {
        for (int k = 0; k < n; ++k) {
          int dx1 = x[sort_idx[j]] - x[sort_idx[i]];
          int dy1 = y[sort_idx[j]] - y[sort_idx[i]];
          int dx2 = x[sort_idx[k]] - x[sort_idx[i]];
          int dy2 = y[sort_idx[k]] - y[sort_idx[i]];
          area[i][j][k] = dx1 * dy2 - dy1 * dx2;
        }
      }
    }
    auto Between = [&](int i, int j, int k) {
      return (x[sort_idx[i]] - x[sort_idx[j]]) *
                     (x[sort_idx[i]] - x[sort_idx[k]]) <=
                 0 &&
             (y[sort_idx[i]] - y[sort_idx[j]]) *
                     (y[sort_idx[i]] - y[sort_idx[k]]) <=
                 0;
    };

    auto Prob = [&](int i) { return prob[sort_idx[i]] / 1000.0; };

    auto TotalProb = [&](int a, int b, int c) {
      double p = Prob(a) * Prob(b) * Prob(c);
      for (int i = 0; i < n; ++i) {
        if (i == a || i == b || i == c) {
          continue;
        }
        if (i < a || area[b][c][i] < 0 ||
            (area[b][c][i] == 0 && Between(i, b, c))) {
          p *= 1.0 - Prob(i);
        }
      }
      return p;
    };
    double result = 0.0;
    for (int i = 0; i < n; ++i) {
      for (int j = i + 1; j < n; ++j) {
        for (int k = i + 1; k < n; ++k) {
          if (j != k && area[i][j][k] > 0) {
            result += area[i][j][k] * 0.5 * TotalProb(i, j, k);
          }
        }
      }
    }
    return result;
  }
};