LTI系统,已知系统输入和输出,求脉冲响应
https://www.ilovematlab.cn/forum.php?mod=viewthread&tid=298897&ordertype=1&_dsign=961ef8cf
问题描述:一个LTI系统,输入序列为x(n),输出序列是y(n),均已知。求系统的脉冲响应。
我的思路是这样的:
设系统响应为h(n),那么有:
y(n) = x(n)*h(n)
即是将输入信号和脉冲响应做卷积,得到输出信号。
两边做fft,有:
Y(w) = X(w).*H(w)
则有:
H(w) = Y(w)./X(w)
然后两边再同时取ifft。左边即是h(n).
也就是说,要求h(n),我们只需要求得y(n)和x(n)的fft,然后做点除,最后做ifft即可。
——实际上,是这样的么?
我用下面的例子验证:
clear,clc
f = 64;
fs = 1024;
n = 0:1/fs:1-1/fs;
len = length(n);
x = sin(2*pi*f*n);
xw = fft(x,len);
xw1_inv = 1./xw;
h = [1 2 3 4 ];
y = conv(x,h);
h1 = ifft(fft(y,len).*xw1_inv,'symmetric');
figure
stem(h1)
我想先用x(n)和h(n)做卷积得到y(n),然后用上面的方法,将y(n)和x(n)做fft后点除,再ifft解出h(n).
但是,结果却完全是乱的。不仅值不等,连长度也不等!原来脉冲响应是4点的,得到的h1是频谱长度的,因为ifft反解时点数默认是和频谱点数相等。改为
h1 = ifft(fft(y,len).*xw1_inv,4,'symmetric');
还是不等。
那么,我的问题出在哪里?是原来的推理不对,还是验证的编程不对呢?恳请大家指教。谢谢。
这里的线性卷积不知道有没问题,这个例子固然没问题,但是当我将脉冲响应变的很长时,会有计算不准出现。具体实验这里没记录下来。
有些地方说如果输入是周期信号,那么这里要用圆周卷积。但没有详细介绍。
关于已知系统输入和输出求解脉冲响应的问题,应该还有诸多解法,比如用胡功率谱和自功率谱法。欢迎大家指教、讨论。
另外,如果有人在做正弦扫频信号测量系统频率响应相关课题,可以深入研讨。
还是自己回复了吧,最近人品不够,发帖连个回音都没。在别的地方发了一下,还好有人讨论下。自己想了一下,应该是解决了。同意的记得点赞哈 呵呵
程序修改如下:
f = 64;
fs = 1024;
n = 0:1/fs:1-1/fs;
len1 = length(n);
x = sin(2*pi*f*n);
h = [1 2 3 4 ];
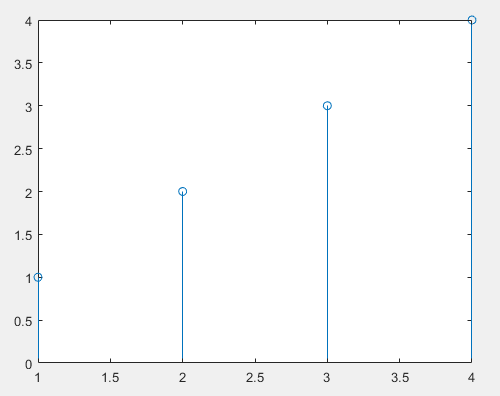
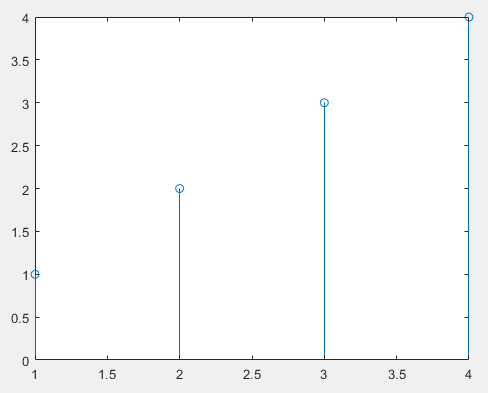
stem(h);
y = conv(x,h);
len2 = length(y);
xw = fft(x,len2);
xw1_inv = 1./xw;
h1 = ifft(fft(y,len2).*xw1_inv,'symmetric');
figure
stem(h1(1:len2-len1+1))
两个图一样,这个问题应该算解决了吧。原帖出错的原因是,时域信号做线性卷积,对应到频域就是扩展的点乘,也就是将激励和响应先补零(按照线性卷积长度)再变换到频域,再点乘。而在最后恢复响应时,将算得的响应后面的一定长度(激励的长度)去掉即可。这应该算一种计算脉冲响应你的方法吧。查阅一些资料上,有直接用矩阵逆运算的,或者说是逐步迭代反解。借助于matlab的卷积和fft、iff,这种方法应该要方便和实用多了。
还是自己回复了吧,最近人品不够,发帖连个回音都没。在别的地方发了一下,还好有人讨论下。自己想了一下,应该是解决了。同意的记得点赞哈 呵呵
程序修改如下:
f = 64;
fs = 1024;
n = 0:1/fs:1-1/fs;
len1 = length(n);
x = sin(2*pi*f*n);
h = [1 2 3 4 ];
stem(h);
y = conv(x,h);
len2 = length(y);
xw = fft(x,len2);
xw1_inv = 1./xw;
h1 = ifft(fft(y,len2).*xw1_inv,'symmetric');
figure
stem(h1(1:len2-len1+1))
两个图一样,这个问题应该算解决了吧。原帖出错的原因是,时域信号做线性卷积,对应到频域就是扩展的点乘,也就是将激励和响应先补零(按照线性卷积长度)再变换到频域,再点乘。而在最后恢复响应时,将算得的响应后面的一定长度(激励的长度)去掉即可。这应该算一种计算脉冲响应你的方法吧。查阅一些资料上,有直接用矩阵逆运算的,或者说是逐步迭代反解。借助于matlab的卷积和fft、iff,这种方法应该要方便和实用多了。
还是自己回复了吧,最近人品不够,发帖连个回音都没。在别的地方发了一下,还好有人讨论下。自己想了一下,应该是解决了。同意的记得点赞哈 呵呵
程序修改如下:
f = 64;
fs = 1024;
n = 0:1/fs:1-1/fs;
len1 = length(n);
x = sin(2*pi*f*n);
h = [1 2 3 4 ];
stem(h);
y = conv(x,h);
len2 = length(y);
xw = fft(x,len2);
xw1_inv = 1./xw;
h1 = ifft(fft(y,len2).*xw1_inv,'symmetric');
figure
stem(h1(1:len2-len1+1))
两个图一样,这个问题应该算解决了吧。原帖出错的原因是,时域信号做线性卷积,对应到频域就是扩展的点乘,也就是将激励和响应先补零(按照线性卷积长度)再变换到频域,再点乘。而在最后恢复响应时,将算得的响应后面的一定长度(激励的长度)去掉即可。这应该算一种计算脉冲响应你的方法吧。查阅一些资料上,有直接用矩阵逆运算的,或者说是逐步迭代反解。借助于matlab的卷积和fft、iff,这种方法应该要方便和实用多了。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 字符编码:从基础到乱码解决
2020-05-17 用变分推断统一理解深度生成模型
2020-05-17 pytorch Windows常见问题汇总
2020-05-17 深度卷积网络中如何进行上采样?