Fréchet距离度量

Fréchet distance

Fréchet distance经常被用于描述路径相似性。

 

Fréchet distance(弗雷歇距离)是法国数学家Maurice René Fréchet在1906年提出的一种路径空间相似形描述( 此外还在这篇论文里定义了 度量空间)，这种描述同时还考虑进路径空间距离的因素[1]，对于空间路径的相似性比较适用。

[1] Fréchet, M. Maurice. "Sur quelques points du calcul fonctionnel." Rendiconti del Circolo Matematico di Palermo (1884-1940) 22.1 (1906): 1-72.

 

直观的理解，Fréchet distance就是最短的狗绳长度：主人走路径A，狗走路径B，各自走完这两条路径过程中所需要的最短狗绳长度。

Fréchet distance的直观理解

在数学中，Fréchet距离是曲线之间相似性的度量，它考虑了沿曲线的点的位置和顺序。它以Maurice Fréchet命名。

Intuitive definition

Imagine a person traversing a finite curved path while walking their dog on a leash, with the dog traversing a separate finite curved path. Each can vary their speed to keep slack in the leash, but neither can move backwards. The Fréchet distance between the two curves is the length of the shortest leash sufficient for both to traverse their separate paths from start to finish. Note that the definition is symmetric with respect to the two curves—the Fréchet distance would be the same if the dog were walking its owner.

想象一下，一个人用皮带牵着狗走在一条有限弯曲的路径上，而狗走在另一条有限弯曲的路径上。人和狗都可以改变速度来放松皮带，但都不能后退。两条曲线之间的Fréchet距离是最短的狗绳长度，该长度足以让人和狗从起点到终点穿越各自的路径。请注意，这个定义关于两条曲线是对称的， Fréchet距离将是相同的，如果看作狗是在遛它的主人~。

 

直观地看， Fréchet距离是狗绳的最短长度，同时也是两条曲线之间最大的距离。

Formal definition

 从严格的数学定义上看，Fréchet距离被定义为两条曲线A（alpha(t)）和B（beta(t)）之间距离最大值的下确界。如何理解这句话？

我们可以将t理解为时间，alpha(t)和beta(t)控制人和狗的速度，那么A（alpha(t)）和B（beta(t)）就代表t时刻人和狗的位置。现在人和狗要穿越各自的路径（曲线），因为人和狗的速度是可以任意调整的（即，alpha(t)和beta(t)两个映射是任意的）（我们假设狗绳可以无限伸长），所以必然存在很多种方式可以做到人和狗穿越各自的路径。在每一种速度方案下都能计算该方案下穿越路径时人狗之间的最大值，这个最大值是变的，其取决于二者的速度方案。但是可以想象，在所有的速度方案中一定已存在一种（狗绳）最紧的方式。也就是Fréchet距离取的是距离最大值的下确界。

Fréchet度量考虑到了两条曲线的流动，因为其距离对Fréchet距离有贡献的点对沿着各自的曲线连续扫过。这使得Fréchet距离比任意点集的Hausdorff距离等替代品更能衡量曲线的相似性。两条曲线有可能有较小的Hausdorff距离，但有较大的Fréchet距离。

另一种直观的理解方式是，将两条曲线看做是两条河流，现在从各自的端点开始开闸放水，考察两条河流水头之间的距离。因为我们可以调整每次开闸放水两条河流水头的速度，这样就有不同的组合方案。Fréchet距离取的是不同速度方案下水头之间距离最大值的下确界。

 

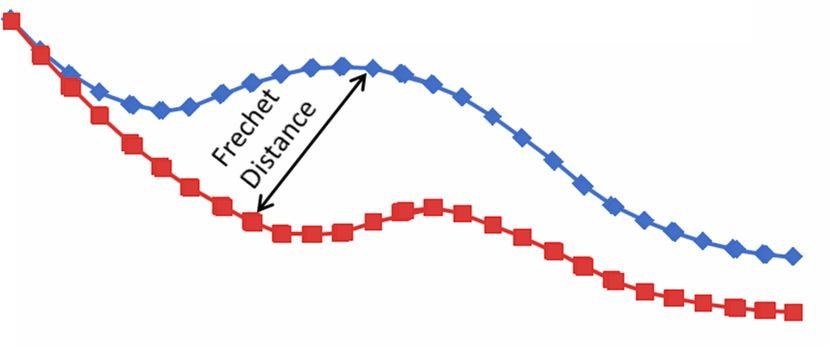
对于Fréchet距离，这两条曲线的长度不一定相同（对于离散情况下，不要求两条曲线包含相同数量的点，两条曲线的点集数目不一定相等）。

 

该距离度量的严格定义参考：

路径相似性描述：Fréchet distance

 

离散化Fréchet distance

 

两个离散序列之间的Fréchet distance

 

关于Discrete Fréchet Distance的计算参考：

T. Eiter, H. Mannila, Computing Discrete Fréchet Distance, Tech. Report CD-TR 94/64, Information Systems Department, Technical University of Vienna, 1994.

 

 matlab实现（待验证）

https://www.mathworks.com/matlabcentral/fileexchange/41956-frechet-distance-calculator

%Tristan Ursell
%Frechet Distance between two curves
%May 2013
%
% f = frechet(X1,Y1,X2,Y2)
% f = frechet(X1,Y1,X2,Y2,res)
%
% (X1,Y1) are the x and y coordinates of the first curve (column vector).
% (X2,Y2) are the x and y coordinates of the second curve (column vector).
%
% The lengths of the two curves do not have to be the same.
%
% 'res' is an optional parameter to set the resolution of 'f', the time to
% compute scales linearly with 'res'. 'res' must be positive, and if 'res'
% is larger than the largest distance between any two points on the curve
% the function will throw a warning. If 'res' is unspecified, the function
% will select a reasonable value, given the inputs.
%
% This function estimates the Frechet Distance, which is a measure of the
% dissimilarity between two curves in space (in this case in 2D).  It is a
% scalar value that is symmetric with respect to the two curves (i.e. 
% switching X1->X2 and Y1->Y2 does not change the value).  Roughly 
% speaking, this distance metric is the minimum length of a line that
% connects a point on each curve, and allows one to traverse both curves
% from start to finish.  (wiki:  Frechet Distance)
%
% The function requires column input vectors, and the function 'bwlabel' 
% from the image processing toolbox.
%
%
%EXAMPLE: compare three curves to find out which two are most similar
%
% %curve 1
%t1=0:1:50;
%X1=(2*cos(t1/5)+3-t1.^2/200)/2;
%Y1=2*sin(t1/5)+3;
%
% %curve 2
%X2=(2*cos(t1/4)+2-t1.^2/200)/2;
%Y2=2*sin(t1/5)+3;
%
% %curve 3
%X3=(2*cos(t1/4)+2-t1.^2/200)/2;
%Y3=2*sin(t1/4+2)+3;
%
%f12=frechet(X1',Y1',X2',Y2');
%f13=frechet(X1',Y1',X3',Y3');
%f23=frechet(X2',Y2',X3',Y3');
%f11=frechet(X1',Y1',X1',Y1');
%f22=frechet(X2',Y2',X2',Y2');
%f33=frechet(X3',Y3',X3',Y3');
%
%figure;
%subplot(2,1,1)
%hold on
%plot(X1,Y1,'r','linewidth',2)
%plot(X2,Y2,'g','linewidth',2)
%plot(X3,Y3,'b','linewidth',2)
%legend('curve 1','curve 2','curve 3','location','eastoutside')
%xlabel('X')
%ylabel('Y')
%axis equal tight
%box on
%title(['three space curves to compare'])
%legend
%
%subplot(2,1,2)
%imagesc([[f11,f12,f13];[f12,f22,f23];[f13,f23,f33]])
%xlabel('curve')
%ylabel('curve')
%cb1=colorbar('peer',gca);
%set(get(cb1,'Ylabel'),'String','Frechet Distance')
%axis equal tight
%

function f = frechet(X1,Y1,X2,Y2,varargin)

%get path point length
L1=length(X1);
L2=length(X2);

%check vector lengths
if or(L1~=length(Y1),L2~=length(Y2))
    error('Paired input vectors (Xi,Yi) must be the same length.')
end

%check for column inputs
if or(or(size(X1,1)<=1,size(Y1,1)<=1),or(size(X2,1)<=1,size(Y2,1)<=1))
    error('Input vectors must be column vectors.')
end

%create maxtrix forms
X1_mat=ones(L2,1)*X1';
Y1_mat=ones(L2,1)*Y1';
X2_mat=X2*ones(1,L1);
Y2_mat=Y2*ones(1,L1);

%calculate frechet distance matrix
frechet1=sqrt((X1_mat-X2_mat).^2+(Y1_mat-Y2_mat).^2);
fmin=min(frechet1(:));
fmax=max(frechet1(:));

%handle resolution
if ~isempty(varargin)
    res=varargin{1};
    if res<=0
        error('The resolution parameter must be greater than zero.')
    elseif ((fmax-fmin)/res)>10000
        warning('Given these two curves, and that resolution, this might take a while.')
    elseif res>=(fmax-fmin)
        warning('The resolution is too low given these curves to compute anything meaningful.')
        f=fmax;
        return
    end
else
    res=(fmax-fmin)/1000;
end

%compute frechet distance
for q3=fmin:res:fmax
    im1=bwlabel(frechet1<=q3);
    
    %get region number of beginning and end points
    if and(im1(1,1)~=0,im1(1,1)==im1(end,end))
        f=q3;
        break
    end
end

　　

Fréchet Inception Distance

除了测量曲线之间的距离外，Fréchet距离还可以用来测量概率分布之间的差异。As a distance between probability distributions (the FID score)

 

Fréchet Inception Distance简称FID最近被提出用于评估生成模型的质量，如生成的图片。

FID was introduced by Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler and Sepp Hochreiter in "GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium", see https://arxiv.org/abs/1706.08500

 

FID is a measure of similarity between two datasets of images. It was shown to correlate well with human judgement of visual quality and is most often used to evaluate the quality of samples of Generative Adversarial Networks. FID is calculated by computing the Fréchet distance between two Gaussians fitted to feature representations of the Inception network.

FID是两个图像数据集之间相似度的度量。它被证明与人类对视觉质量的判断有很好的相关性，并且最常被用于评估生成式对抗网络样本的质量。FID是通过计算拟合到Inception网络特征表示的两个高斯函数之间的Fréchet距离来计算的。

 

 

 

FID得分在Pytorch中的实现参考：

https://github.com/mseitzer/pytorch-fid

 

 

参考：

路径相似性描述：Fréchet distance

https://en.wikipedia.org/wiki/Fréchet_distance