PCA Biplot含义

PCA biplot = PCA score plot + loading plot

matlab PCA分析命令：

[coeff,score,latent,tsquared,explained,mu] = pca(X);

　　

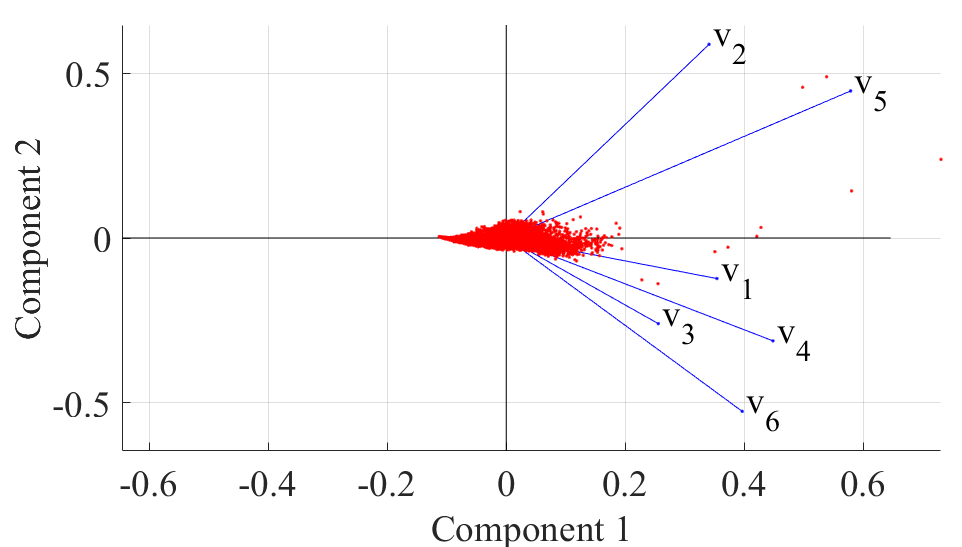
前两个主成分的PCA Biplot

如上图所示，PCA Biplot包含两部分。首先是loading plot，这里loading即PCA变换系数。这里有6个变量（X的维度为6），返回的loading为：

coeff =

    0.3541   -0.1231    0.2676    0.1314    0.6925   -0.5396
    0.3408    0.5872    0.6770    0.0068   -0.2737    0.0759
    0.2556   -0.2597    0.1699   -0.0613    0.4066    0.8181
    0.4483   -0.3120   -0.1127    0.7449   -0.3655    0.0218
    0.5788    0.4460   -0.6410   -0.2127    0.0952    0.0306
    0.3965   -0.5257    0.1328   -0.6154   -0.3710   -0.1800

　　ps: loading矩阵是正交的（coeff * coeff' = I）。

上面PCA Biplot中考虑前两个主成分，绘制loading plot时取coeff的前两列。可以看到，第二行和第五行两个坐标均为正，因此，PCA Biplot中V2, V5在第一象限。其余行均为一正一负，因此V1, V3, V4, V6均位于第四象限。

其次是，score plot，这里score指的是主成分值（即输入X经过loading矩阵变换后的值，也称为潜变量）。这里仅考虑前两个主成分，绘制即可。上图红色的散点即是score plot。

Please note that both the scores and the loadings are scaled to a maximum value of 1.0.

请注意，score和loading都被缩放到1.0的最大值。

PCA biplot含义

从PCA biplot可以看出什么？

1. 各变量间的相关性

V1至V6之间的夹角表示各维度间的相关性，从上图看出，各变量间夹角均小于90度，说明他们呈正相关。（等于90度，没有明确的相关关系，大于90度，负相关关系）

2. 各变量对前两个主成分的贡献

V1-V6的径向长度表示影响的大小，方向表示正负。如，6个变量均对第一主成分有正的影响，V2, V5对第二主成分有正的响应，V1, V3, V4, V6对第二主成分有负的响应。

3. 主成分的变化性

可以看到第一主成分具有最大的方差，第二主成分变化性显著减弱。

4. score的分布

从上图看出除了一些离群点外，score的分布较为紧凑，说明所有样本对系统的反应较为一致。

 

A biplot simultaneously plots information on the observations and the variables in a multidimensional dataset.

A biplot can optimally represent any two of the following characteristics:

• distances between observations
• relationships between variables
• inner products between observations and variables

 

 训练集中异常值对Biplot的影响

发现训练集中如果存在离群值则会对Biplot有较大的影响。Biplot中的点会随着训练集比率的增大逐渐发生偏斜。

 

训练集比率：10%

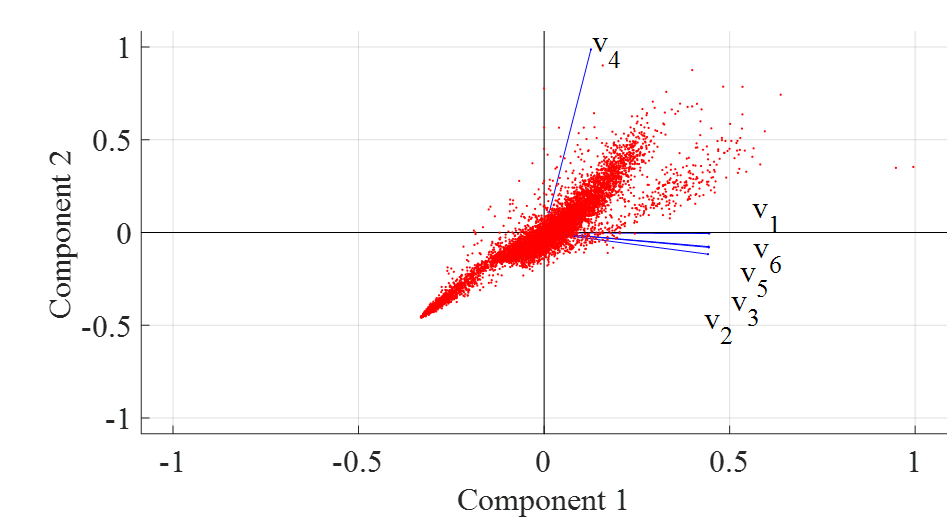
训练集比率：20%

 如上图所示，训练集比率增大后Biplot发生显著变化。经检查后发现，因为数据集中存在部分离群点，当训练集比率增大时，训练集中会引入更多的异常点，这导致训练集统计属性发生改变。

为了避免发生上述现象，可以将训练集中的异常样本剔除，这样训练集样本更具有代表性，刻画的数据分布更准确。

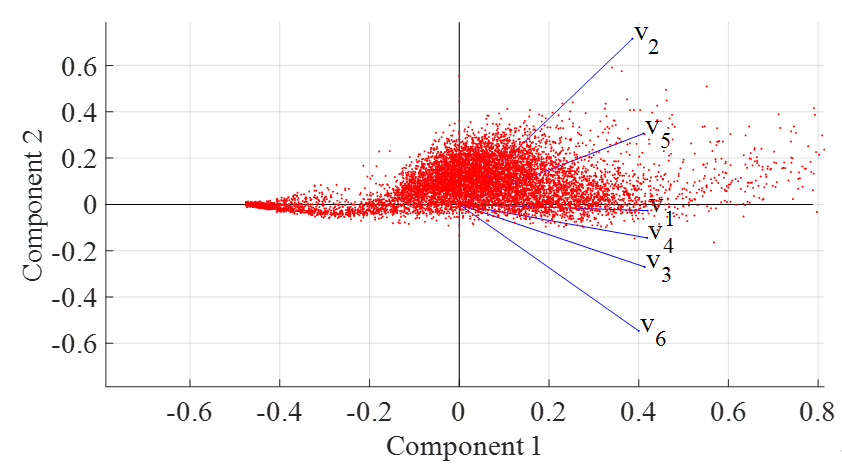
 训练集比率：20%（剔除训练集离群值）