皮尔逊相关系数和余弦相似性的关系
皮尔逊相关系数和余弦相似性的关系
先上结论:在数据标准化( )后,Pearson相关性系数、Cosine相似度、欧式距离的平方可认为是等价的。详细推导在这里。
如何理解皮尔逊相关系数(Pearson Correlation Coefficient)? - 微调的回答 - 知乎
有两种理解方式
(1)皮尔逊相关系数是数据中心化后的余弦相似性;
(2)皮尔逊相关系数可以看做是协方差(定性相关关系)的一种改进,其消除了方差的影响(定量相关关系)。
1. 皮尔逊相关系数是数据中心化后的余弦相似性
作者:陈小龙
链接:https://www.zhihu.com/question/19734616/answer/174098489
两个向量之间的夹角余弦等于二者之间的内积除以二者模的乘积。
cos<a, b> = a • b / |a|•|b|
皮尔逊相关系数通过下式计算:

可以看到,二者计算方式类似,皮尔逊相关系数计算时先减去自身的均值(中心化)。
2. 皮尔逊相关系数可以看做是协方差的一种改进
作者:TimXP
链接:https://www.zhihu.com/question/19734616/answer/117730676
要理解Pearson相关系数,首先要理解协方差(Covariance),协方差是一个反映两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值,反之相反,公式如下:

Pearson相关系数公式如下:
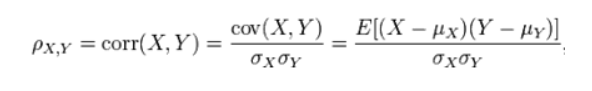
由公式可知,Pearson相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,例如,现在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的,如下图:
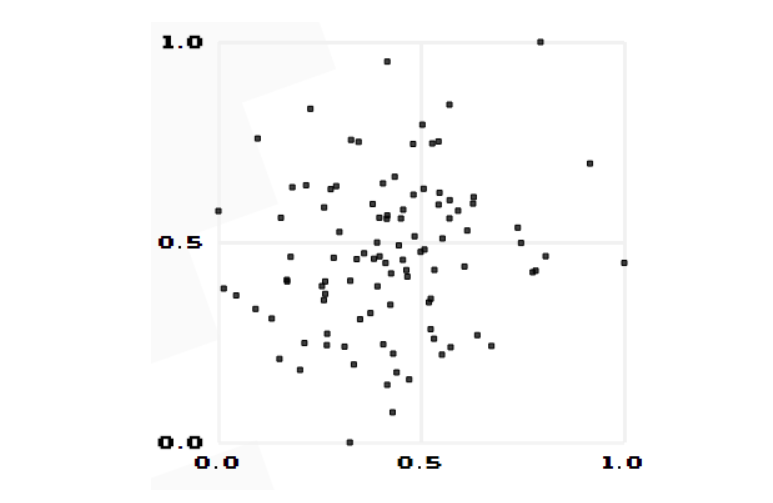
为了更好的度量两个随机变量的相关程度,引入了Pearson相关系数,其在协方差的基础上除以了两个随机变量的标准差,容易得出,pearson是一个介于-1和1之间的值,当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明:
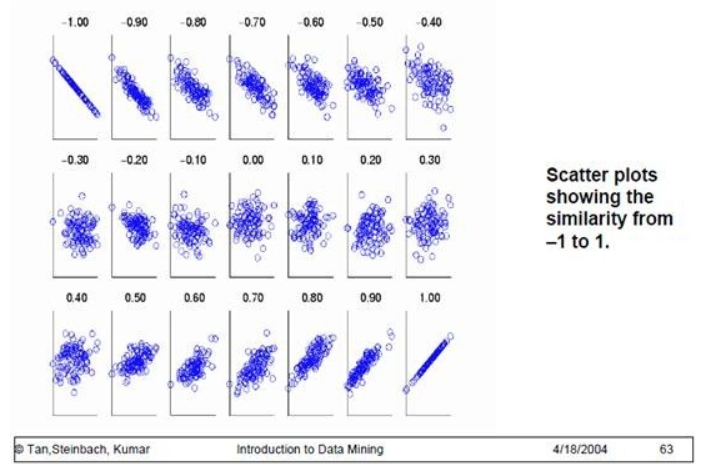
快去成为你想要的样子!



