深度卷积网络中如何进行上采样?
深度学习的许多应用中需要将提取的特征还原到原图像大小,如图像的语义分割、生成模型中的图像生成任务等。通过卷积和池化等技术可以将图像进行降维,因此,一些研究人员也想办法恢复原分辨率大小的图像,特别是在语义分割领域应用很成熟。
常见的上采样方法有双线性插值、转置卷积、上采样(unsampling)、上池化(unpooling)和亚像素卷积(sub-pixel convolution,PixelShuffle)。下面对其进行简单介绍。
一、插值
插值常用的方式有nearest interpolation、bilinear interpolation、bicubic interpolation。
1、nearest interpolation
将离待插值最近的已知值赋值给待插值。
2、bilinear interpolation
根据离待插值最近的 个已知值来计算待插值,每个已知值的权重由距离待插值距离决定,距离越近权重越大。
双线性插值,又称为双线性内插。在数学上,双线性插值是对线性插值在二维直角网格上的扩展,用于对双变量函数(例如 x 和 y)进行插值。其核心思想是在两个方向分别进行一次线性插值。
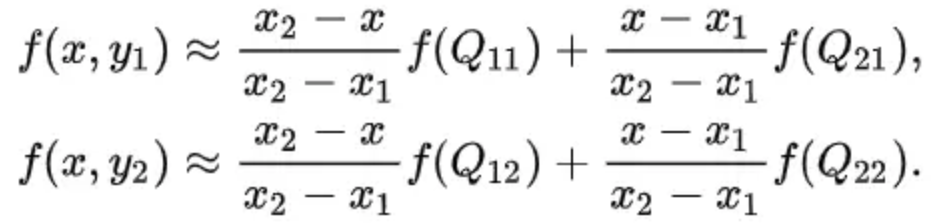
然后在 y 方向进行线性插值,得到 f(x, y):
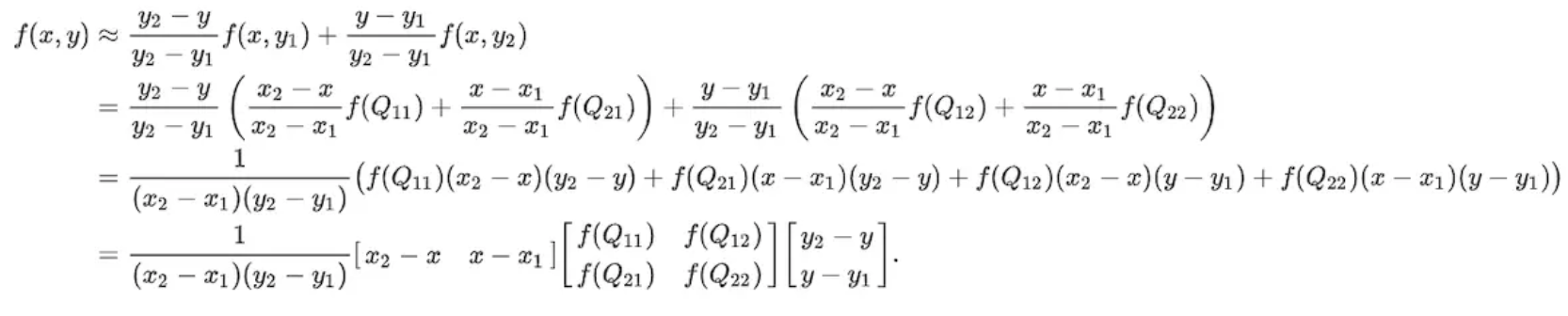
在FCN中上采样用的就是双线性插值。
Fully Convolutional Networks for Semantic Segmentation
3、bicubic interpolation
根据离待插值最近的 个已知值来计算待插值,每个已知值的权重由距离待插值距离决定,距离越近权重越大。
4、各种插值方式的区别与联系
从nearest interpolation、bilinear interpolation到bicubic interpolation,插值所利用的信息越来越多,feature map越来越平滑,但是同时计算量也越来越大,nearest interpolation、bilinear interpolation、bicubic interpolation的区别与联系可见下图示意,其中黑色的点为预测值,其他彩色点为周围已知值,用来计算预测值。
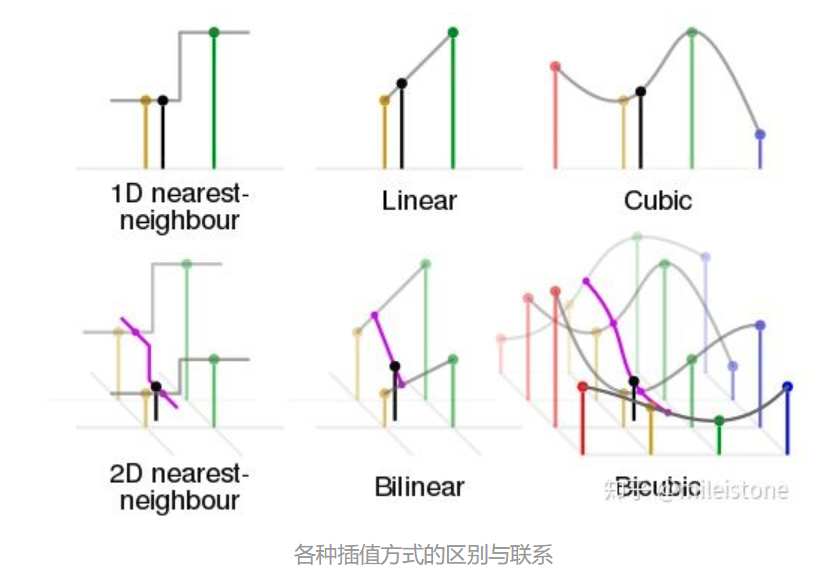
以上的这些方法都是一些插值方法(上采样(up-sampling)操作),需要我们在决定网络结构的时候进行挑选。这些方法就像是人工特征工程一样,并没有给神经网络学习的余地,神经网络不能自己学习如何更好地进行插值,这个显然是不够理想的。
二、上采样(unsampling)
在FCN、U-net等网络结构中,涉及到了上采样。上采样概念:上采样指的是任何可以让图像变成更高分辨率的技术。最简单的方式是重复采样和插值(上面一中的插值属于上采样的一种?):将输入图片进行rescale到一个想要的尺寸,而且计算每个点的像素点,使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。
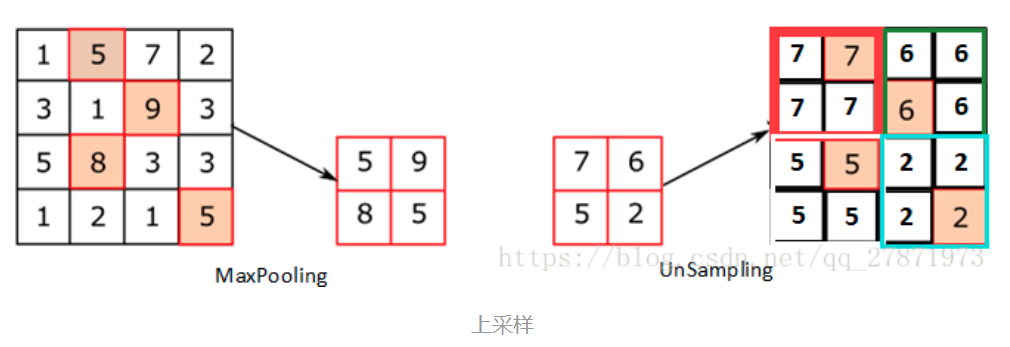
其中右侧为unsampling,可以看出unsampling就是将输入feature map中的某个值映射填充到输出上采样的feature map的某片对应区域中,直接复制或插值。
三、上池化(unpooling)
Unpooling是在CNN中常用的来表示max pooling的逆操作。这是论文《Visualizing and Understanding Convolutional Networks》中产生的思想,下图示意:
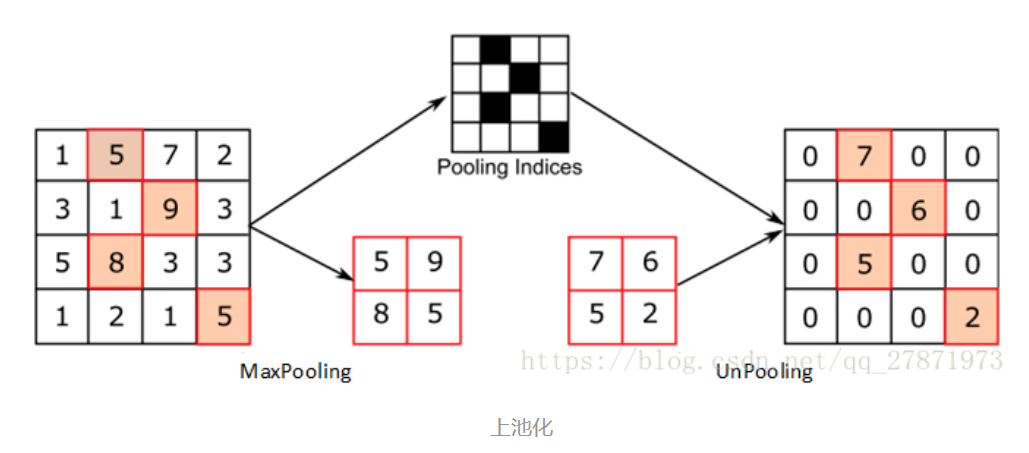
对比上面两个示意图,可以发现区别:
- 两者的区别在于UnSampling阶段没有使用MaxPooling时的位置信息,而是直接将内容复制来扩充Feature Map。第一幅图中右边4*4矩阵,用了四种颜色的正方形框分割为四个区域,每一个区域内的内容是直接复制上采样前的对应信息。
- UnPooling的过程,特点是在Maxpooling的时候保留最大值的位置信息,之后在unPooling阶段使用该信息扩充Feature Map,除最大值位置以外,其余补0。从图中即可看到两者结果的不同。
《Visualizing and Understanding Convolutional Networks》:https://arxiv.org/abs/1311.2901
四、转置卷积/反卷积/逆卷积/分数步长卷积
自从步入深度学习时代,我们越来越追求end2end,那么升采样能不能不用人为定义的权重,而让模型自己学习呢?答案是显然的,deconv就是解决方案之一。在上面的双线性插值方法中不需要学习任何参数。而转置卷积就像卷积一样需要学习参数,关于转置卷积的具体计算可以参见一文搞懂反卷积,转置卷积。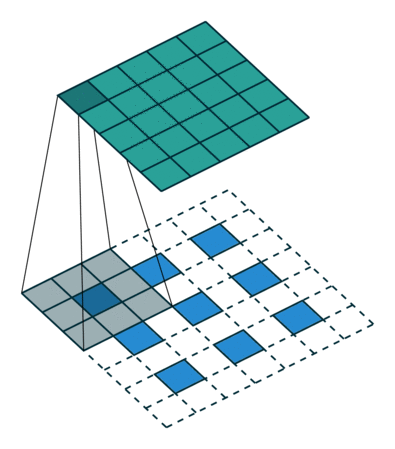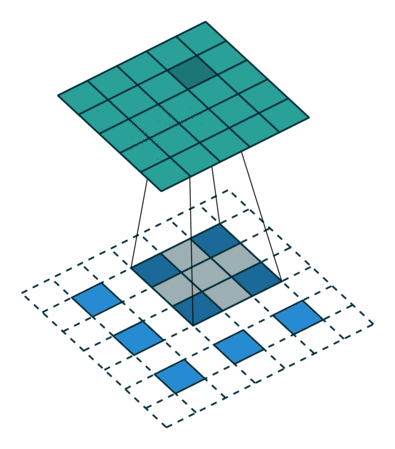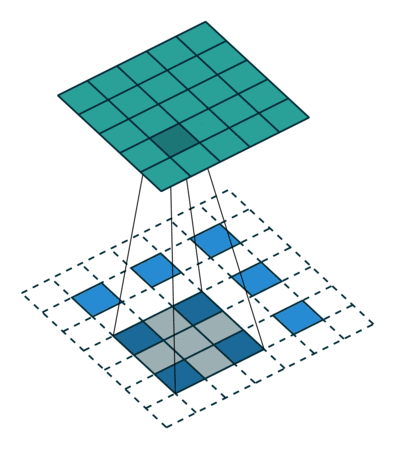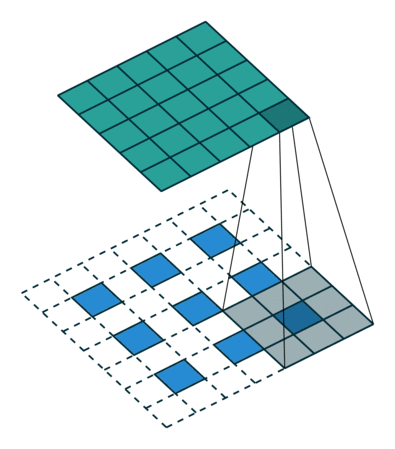
卷积与转置卷积的区别可将卷积表示为矩阵相乘演示:
1、stride=1
等价于stride=1的conv,只是padding方式不同,不能起到升采样的作用。以一维的数据为例,示意图如下,中间步骤是将卷积转换为矩阵乘法的过程。

2、stride > 1
能起到升采样的作用,一般用到的deconv,stride都大于1。以一维的数据为例,示意图如下,中间步骤是将卷积转换为矩阵乘法的过程。

deconvolution也叫transposed convolution,upconvolution等等。其中deconvolution这个名字有点歧义性,容易带来困惑,transposed convolution比较容易理解。容易验证1和2中convolution和deconvolution中的权重矩阵互为转置。
需要注意的是:这里的转置卷积矩阵的参数,不一定从原始的卷积矩阵中简单转置得到的,转置这个操作只是提供了转置卷积矩阵的形状而已。
注意:转置卷积会导致生成图像中出现棋盘效应(checkerboard artifacts),这篇文章《Deconvolution and Checkerboard Artifacts》推荐了一种上采样的操作(也就是插值操作)称为 resize-convolution,这个操作接在一个卷积操作后面以减少这种现象。如果你的主要目的是生成尽可能少棋盘效应的图像,那么这篇文章就值得你去阅读。
计算公式
转置卷积计算过程是将输入的每个元素值作为卷积核的权重,相乘后作为该元素对应的上采样输出,不同输入的重叠的输出部分直接相加作为输出.示意图如下: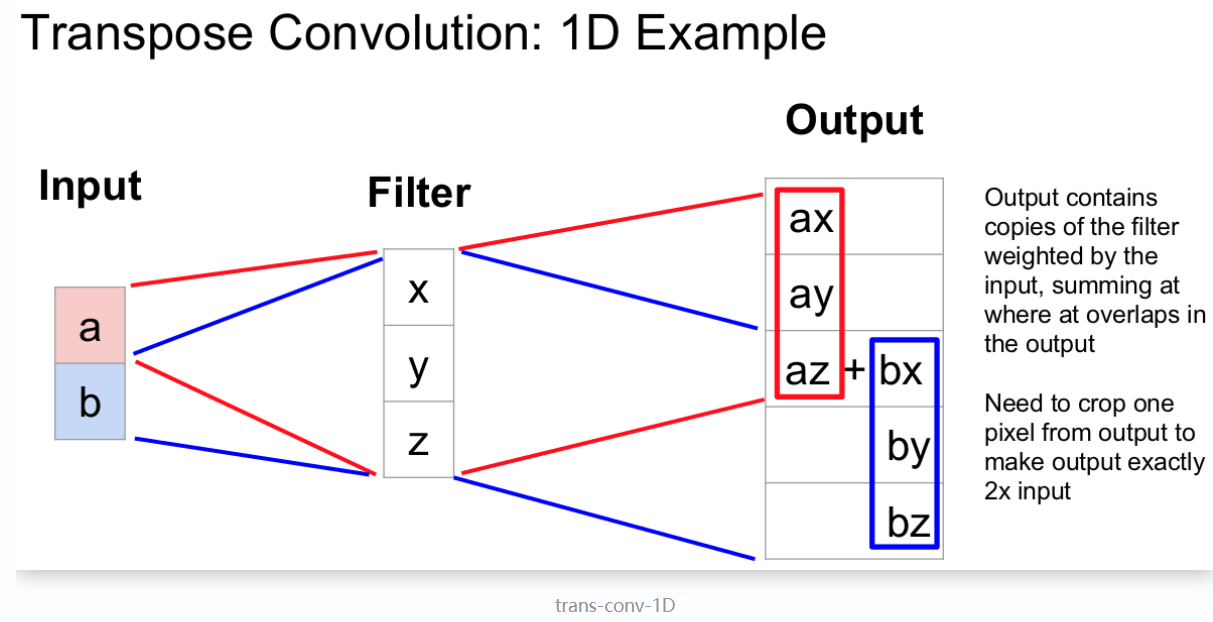
2-D转置卷积操作:在输入的相邻像素间填充stride-1个0,再在边缘填充kernel_size - 1 - crop个 zero-padding,再进行卷积运算。最后一步还要进行裁剪。
转置卷积的运算示意图如下:
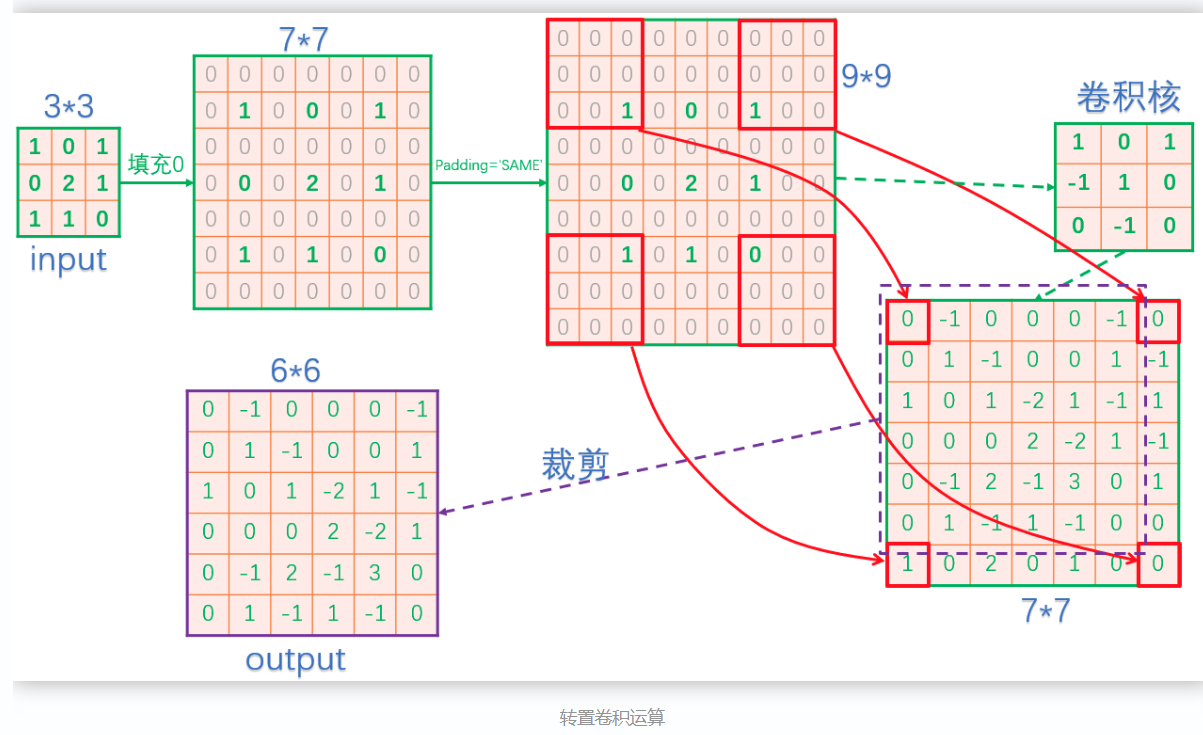
为什么叫转置卷积?
转置卷积也被称为分数步长卷积(Fractionally Strided Convolution),如果前向卷积中步长s>1,那么转置卷积中步长s′<1,但是小于1的步长不能够直接实现,
可以从另外的方式实现:在输入特征单元之间插入 s−1 个0,此时步长 s′ 设置为1,不再是小数。
输入输出尺度关系:

转置卷积的用途
- CNN可视化:通过转置卷积将feature map还原到像素空间,以观察特定的feature map对哪些pattern的图片敏感。
- 上采样:在图像语义分割或生成对抗网络中需要像素级别的预测,需要较高的图像尺寸。
转置卷积的实现
这篇文章采用python给出了转置卷积的一种实现
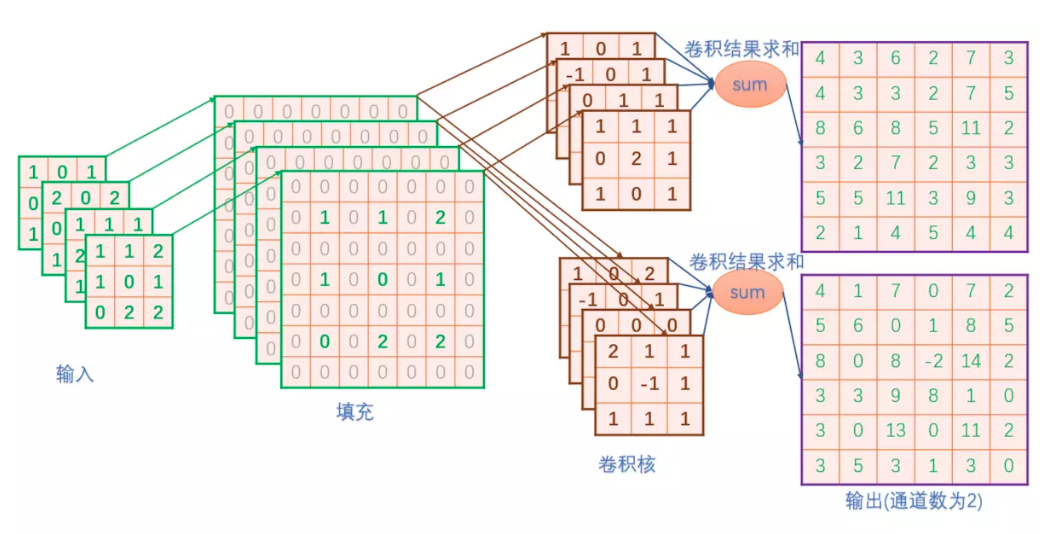
可以看到实际上,反卷积和卷积基本一致,差别在于,反卷积需要填充过程,并在最后一步需要裁剪。具体实现代码如下:
#根据输入map([h,w])和卷积核([k,k]),计算卷积后的feature map import numpy as np def compute_conv(fm,kernel): [h,w]=fm.shape [k,_]=kernel.shape r=int(k/2) #定义边界填充0后的map padding_fm=np.zeros([h+2,w+2],np.float32) #保存计算结果 rs=np.zeros([h,w],np.float32) #将输入在指定该区域赋值,即除了4个边界后,剩下的区域 padding_fm[1:h+1,1:w+1]=fm #对每个点为中心的区域遍历 for i in range(1,h+1): for j in range(1,w+1): #取出当前点为中心的k*k区域 roi=padding_fm[i-r:i+r+1,j-r:j+r+1] #计算当前点的卷积,对k*k个点点乘后求和 rs[i-1][j-1]=np.sum(roi*kernel) return rs #填充0 def fill_zeros(input): [c,h,w]=input.shape rs=np.zeros([c,h*2+1,w*2+1],np.float32) for i in range(c): for j in range(h): for k in range(w): rs[i,2*j+1,2*k+1]=input[i,j,k] return rs def my_deconv(input,weights): #weights shape=[out_c,in_c,h,w] [out_c,in_c,h,w]=weights.shape out_h=h*2 out_w=w*2 rs=[] for i in range(out_c): w=weights[i] tmp=np.zeros([out_h,out_w],np.float32) for j in range(in_c): conv=compute_conv(input[j],w[j]) #注意裁剪,最后一行和最后一列去掉 tmp=tmp+conv[0:out_h,0:out_w] rs.append(tmp) return rs def main(): input=np.asarray(input_data,np.float32) input= fill_zeros(input) weights=np.asarray(weights_data,np.float32) deconv=my_deconv(input,weights) print(np.asarray(deconv)) if __name__=='__main__': main()
为了验证实现的代码的正确性,我们使用tensorflow的conv2d_transpose函数执行相同的输入和卷积核,看看结果是否一致。验证代码如下:
import tensorflow as tf import numpy as np def tf_conv2d_transpose(input,weights): #input_shape=[n,height,width,channel] input_shape = input.get_shape().as_list() #weights shape=[height,width,out_c,in_c] weights_shape=weights.get_shape().as_list() output_shape=[input_shape[0], input_shape[1]*2 , input_shape[2]*2 , weights_shape[2]] print("output_shape:",output_shape) deconv=tf.nn.conv2d_transpose(input,weights,output_shape=output_shape, strides=[1, 2, 2, 1], padding='SAME') return deconv def main(): weights_np=np.asarray(weights_data,np.float32) #将输入的每个卷积核旋转180° weights_np=np.rot90(weights_np,2,(2,3)) const_input = tf.constant(input_data , tf.float32) const_weights = tf.constant(weights_np , tf.float32 ) input = tf.Variable(const_input,name="input") #[c,h,w]------>[h,w,c] input=tf.transpose(input,perm=(1,2,0)) #[h,w,c]------>[n,h,w,c] input=tf.expand_dims(input,0) #weights shape=[out_c,in_c,h,w] weights = tf.Variable(const_weights,name="weights") #[out_c,in_c,h,w]------>[h,w,out_c,in_c] weights=tf.transpose(weights,perm=(2,3,0,1)) #执行tensorflow的反卷积 deconv=tf_conv2d_transpose(input,weights) init=tf.global_variables_initializer() sess=tf.Session() sess.run(init) deconv_val = sess.run(deconv) hwc=deconv_val[0] print(hwc) if __name__=='__main__': main()
上面代码中,有几点需要注意:
- 每个卷积核需要旋转180°后,再传入tf.nn.conv2d_transpose函数中,因为tf.nn.conv2d_transpose内部会旋转180°,所以提前旋转,再经过内部旋转后,能保证卷积核跟我们所使用的卷积核的数据排列一致。
- 我们定义的输入的shape为[c,h,w]需要转为tensorflow所使用的[n,h,w,c]。
- 我们定义的卷积核shape为[out_c,in_c,h,w],需要转为tensorflow反卷积中所使用的[h,w,out_c,in_c]
转置卷积和插值的区别与联系
转置卷积和插值,都是通过周围像素点来预测空白像素点的值,区别在于一个权重由人为预先定义的公式计算,一个通过数据驱动来学习。
一些转置卷积的论文截图
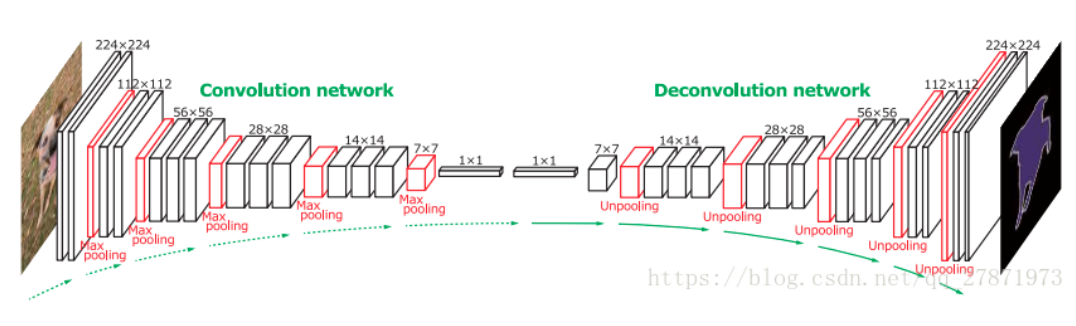
上图为以转置卷积和全卷积网络为核心的语义分割网络。
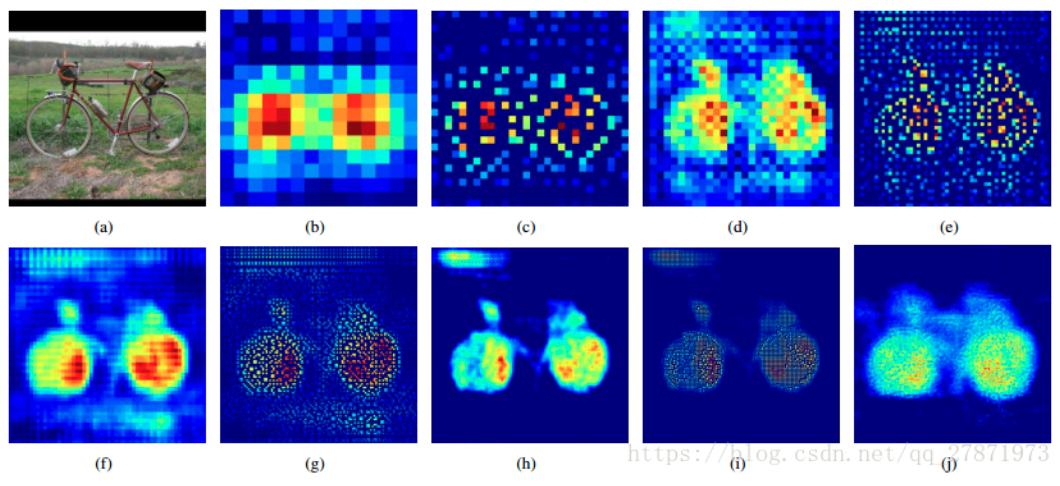
图(a)是输入层;图b、d、f、h、j是不同featrue map大小的转置卷积的结果;图c、e、g、i是不同featrue map大小的UnPooling结果。
《Learning Deconvolution Network for Semantic Segmentation》
五、亚像素卷积(sub-pixel convolution,PixelShuffle)
正常情况下,卷积操作会使feature map的高和宽变小。文章将这个算法描述为:LR network,即低分辨卷积网络。文章拿来与之作对比的是HR network,高分辨卷积网络,一般HR network是现将低分辨力的图像进行二次插值变换后然后对变换后的图像再进行卷积网络。即HR network是先将图像进行upsample后才进行卷积,而文中的这个算法操作则是在upsample的过程中对图像就进行了卷积。
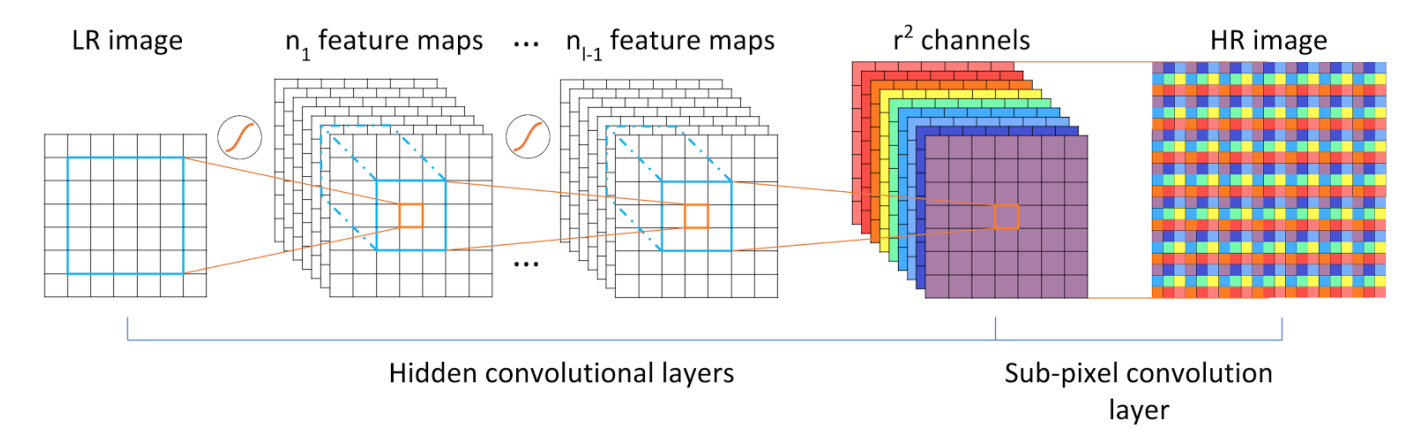
这个算法的实现流程如上图,举个例子,实现的功能就是将一个1×1的image通过Sub-pixel操作将其变为rxr的高分辨率图像,但是这个实现过程不是直接产生这个高分辨率图像而是先得到r2个通道特征图然后通过周期筛选(periodic shuffing)得到这个高分辨率的图像,其中r为upscaling factor,也就是图像扩大倍率。
我们可以说这种操作:一边Upsample一边Convolve,或者说在卷积的同时进行了上采样(因为扩大后的图像来自卷积特征图)。
转置卷积与普通的亚采样卷积
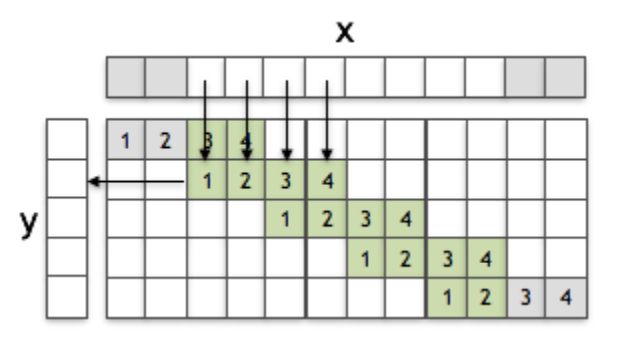
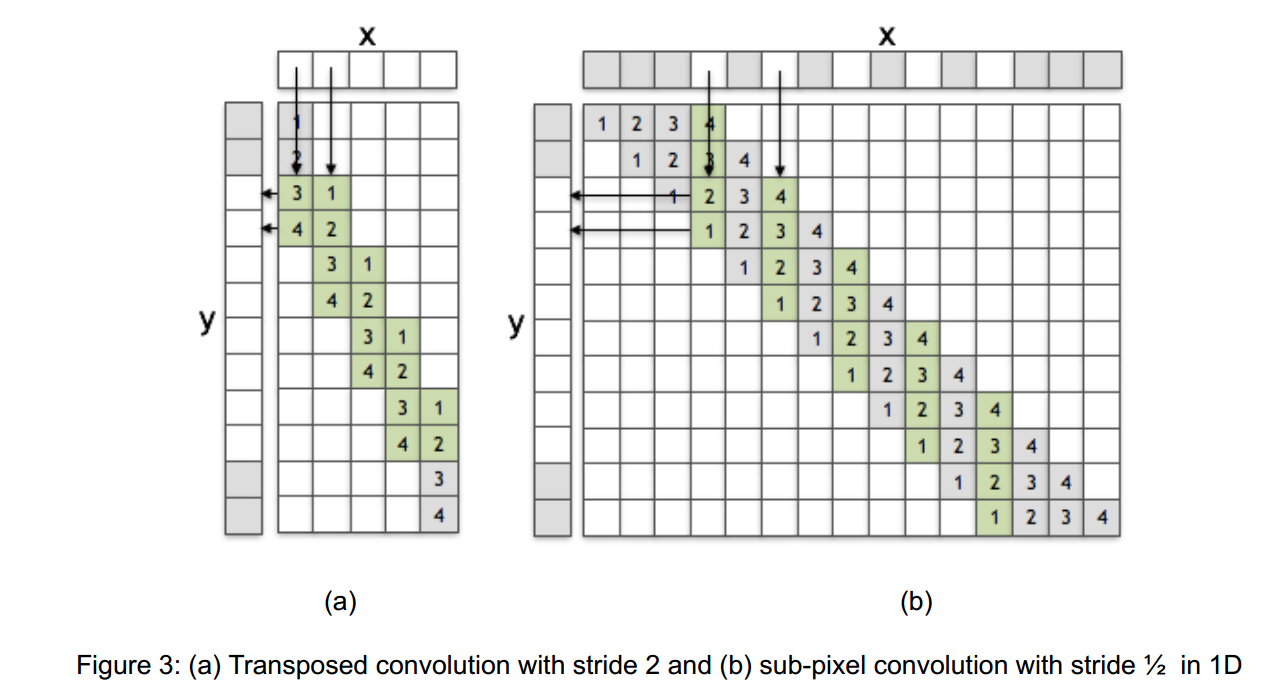
我们可以看到,这两个操作之间的唯一区别是,当从x向y做贡献时,所使用的权重的下标是不同的。如果我们在亚像素卷积中反转滤波器f的元素下标,那么这一层将等于一个转置的卷积层。换句话说,如果学习了过滤器,这两个操作可以得到相同的结果。
Deconvolution layer vs Convolution in LR
从普通亚像素卷积到LR亚像素卷积:
普通亚像素卷积要先进行填充,从LR图像创建亚像素图像
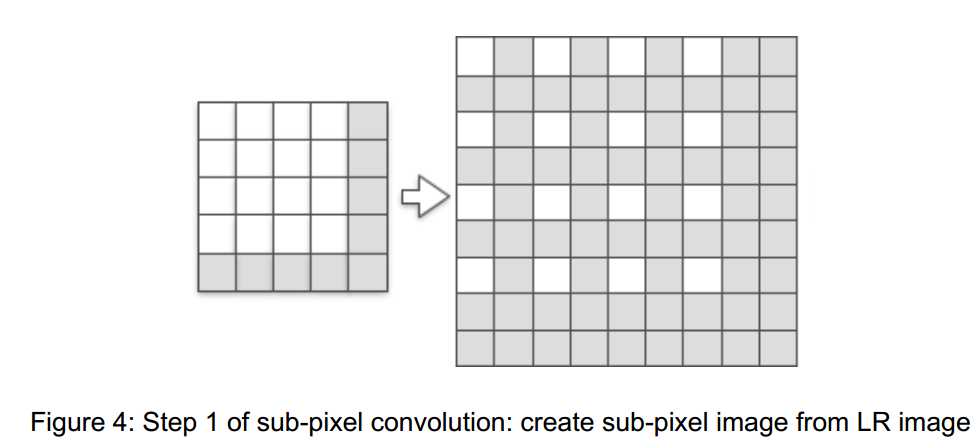
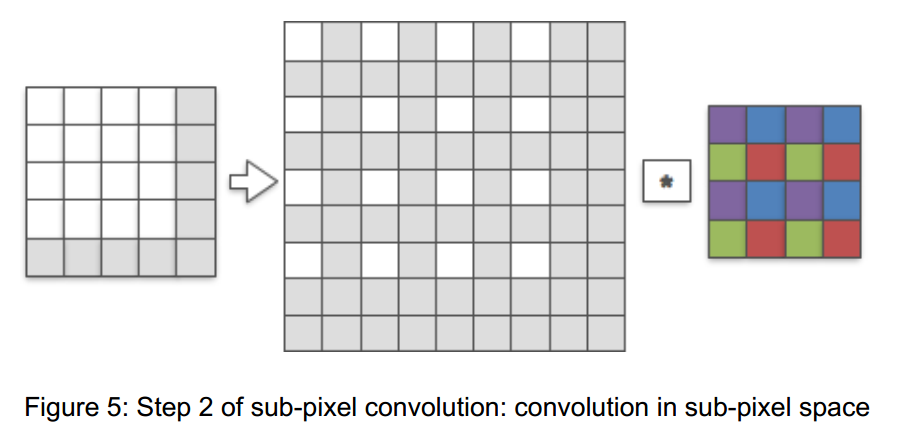
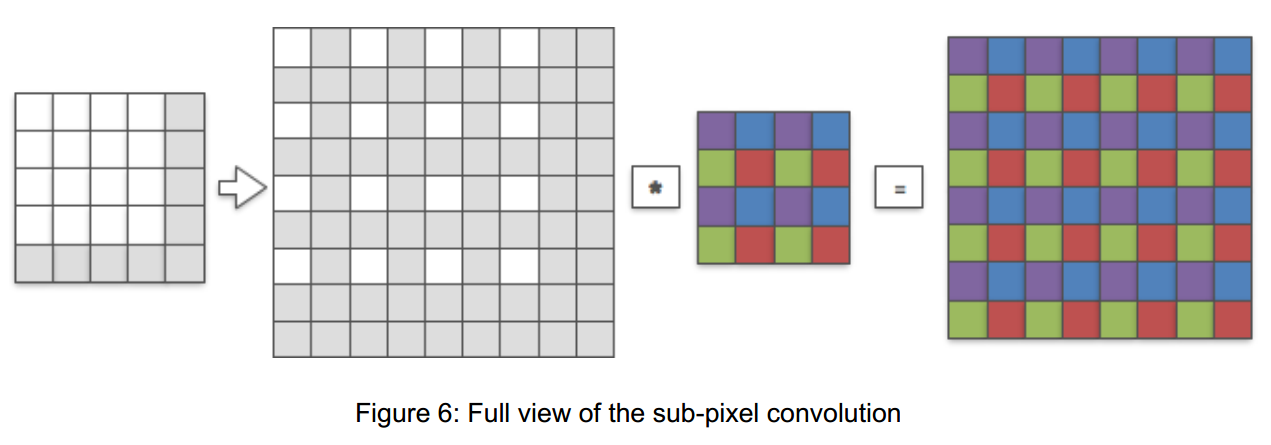
注意到,不同颜色组的卷积核权重进行激活时是相互独立的,因此完全可以将4x4的卷积核分解成4个2x2的小卷积核。
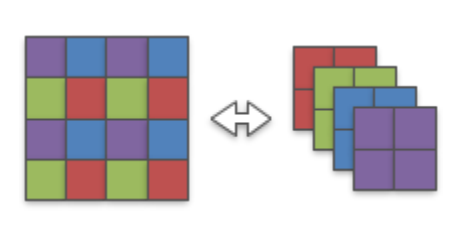
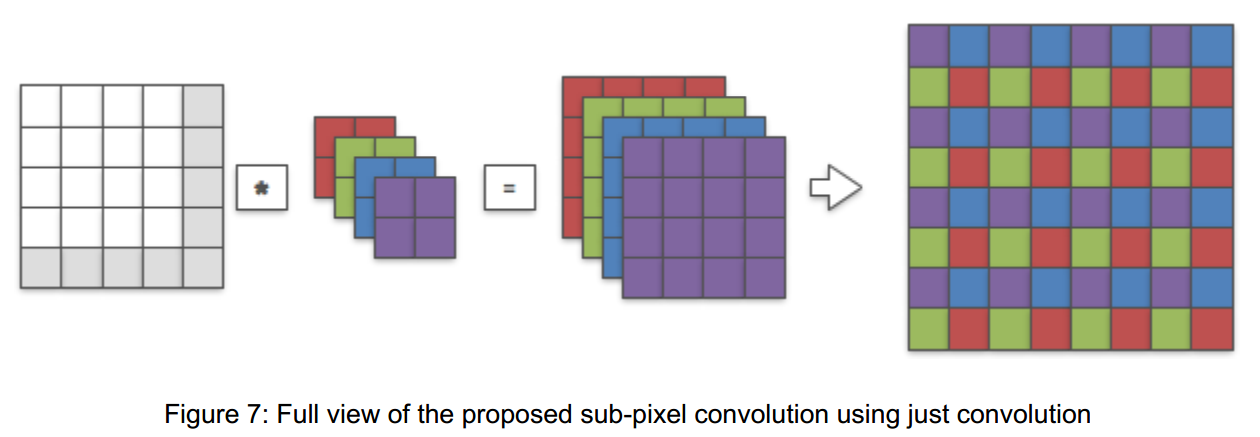
因此,普通的亚像素卷积可以改造成仅使用卷积运算的LR亚像素卷积,最后卷积完将特征图reshape成最终的上采样结果。
What does this mean?
This means that a network can learn to use r2 channels of LR image/feature maps to represent one HR image/feature maps if it is encouraged to do so.
一个网络能够学习使用r2 个channel的LR特征图来表示HR图像,如果它被鼓励这么做。
至于为什么在LR上进行卷积更好,作者在《Is the deconvolution layer the same as a convolutional layer?》给出了一些经验分析。
参考:
[1] https://www.jianshu.com/p/587c3a45df67
[2] https://zhuanlan.zhihu.com/p/41427866
[3] https://blog.csdn.net/qq_27871973/article/details/82973048
[4] https://blog.csdn.net/LoseInVain/article/details/81098502
[5] https://www.cnblogs.com/makefile/p/unpooling.html
[6] https://blog.csdn.net/g11d111/article/details/82855946
[7] https://oldpan.me/archives/upsample-convolve-efficient-sub-pixel-convolutional-layers
posted on 2020-05-17 11:01 那抹阳光1994 阅读(16044) 评论(0) 编辑 收藏 举报



