柯尔莫可洛夫-斯米洛夫检验（Kolmogorov–Smirnov test，K-S test）

K-S检验方法能够利用样本数据推断样本来自的总体是否服从某一理论分布，是一种拟合优度的检验方法，适用于探索连续型随机变量的分布。

Kolmogorov–Smirnov test

Kolmogorov–Smirnov statistic

累计分布函数：

定义n个独立同分布（i.i.d.）有序观测样本Xi的经验分布函数Fn为：

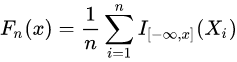
其中 I[−inf,x] 为indicator function（指示函数）， 

 


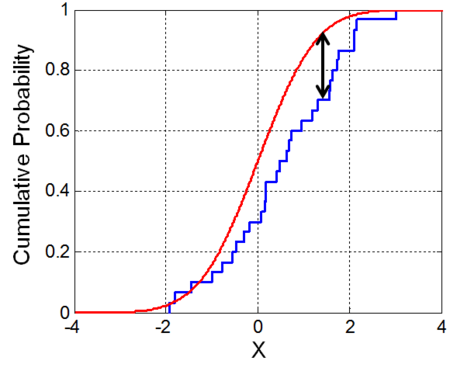
样本集Xi的累计分布函数Fn(x)和一个假设的理论分布F(x)，Kolmogorov–Smirnov统计量定义为： 


 supx是距离的上确界(supremum)， 基于Glivenko–Cantelli theorem（Glivenko–Cantelli theorem），若Xi服从理论分布F(x)，则当n趋于无穷时Dn几乎肯定（almost surely）收敛于0。Kolmogorov通过有效地提供其收敛速度加强了这一结果。Donsker定理（Donsker's theorem ）提供了一个更强的结果。
在实践中，统计量需要相对大量的数据点(与Anderson–Darling test statistic等其他拟合优度标准相比)才能恰当地拒绝零假设。

Kolmogorov distribution

预备知识：

 (1) 独立增量过程 

顾名思义，就是指其增量是相互独立的。严格定义如下： 

 (2) 维纳过程（Wiener process） 

大概可以理解为一种数学化的布朗运动，严格定义如下： 

 (3)布朗桥（Brownian bridge） 

一种特殊的维纳过程，严格定义如下： 

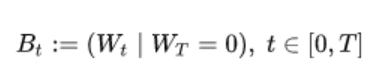
  一个在[0,T]区间上，且WT=0的维纳过程。 

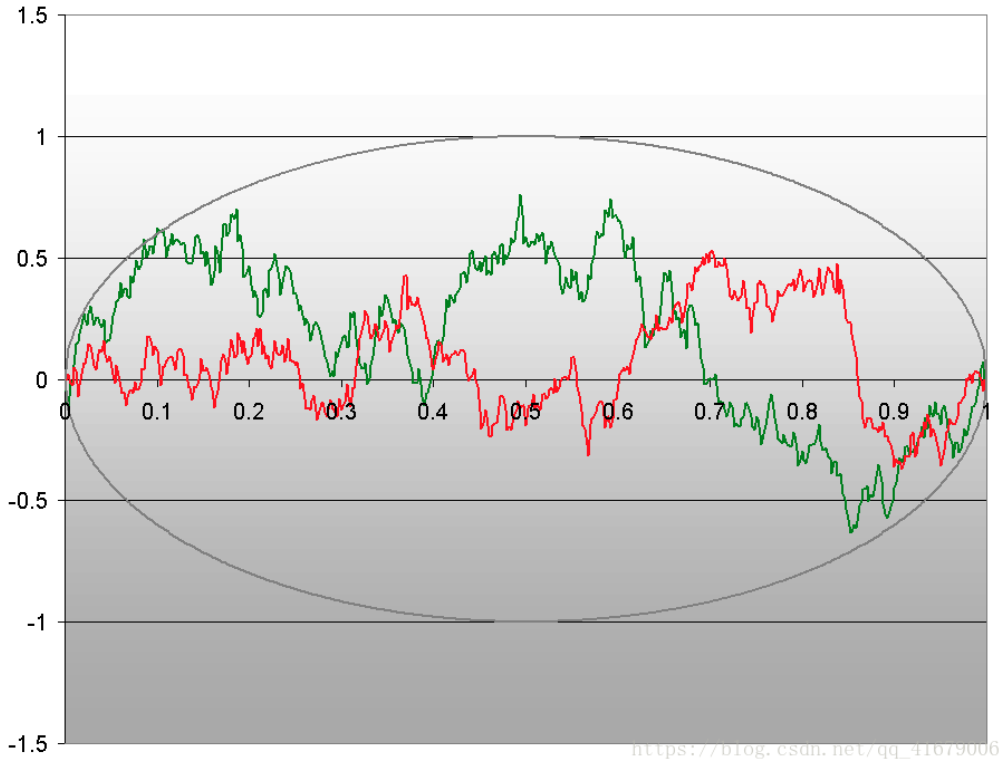
 红色和绿色的都是“布朗桥”。

Kolmogorov distribution

 柯尔莫戈罗夫分布是随机变量K的分布:

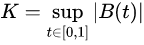
 即是通过求布朗运动上确界得到的随机变量的分布。其中B(t)为布朗桥。

它的累积分布函数可以写为： 

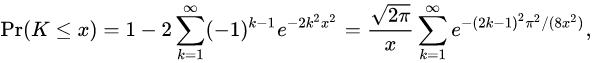
 which can also be expressed by the Jacobi theta function {\displaystyle \vartheta _{01}(z=0;\tau =2ix^{2}/\pi )}. Both the form of the Kolmogorov–Smirnov test statistic and its asymptotic distribution under the null hypothesis were published by Andrey Kolmogorov,[3] while a table of the distribution was published by Nikolai Smirnov.[4] Recurrence relations for the distribution of the test statistic in finite samples are available.[3]

单样本Kolmogorov Goodness-of-Fit Test  

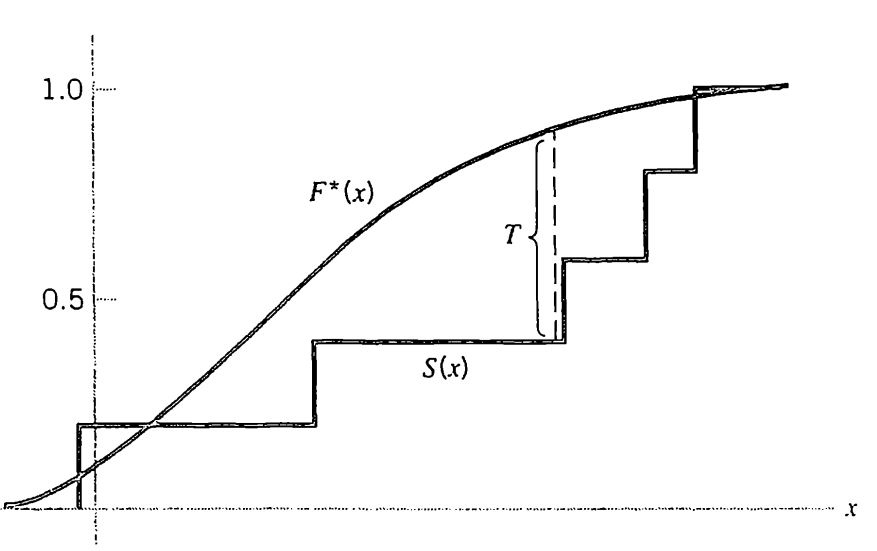
单样本K-S检验即是检验样本数据点是否满足某种理论分布。 

我们从零假设H0出发（ 在样本来自假设分布F(x)的零假设下） ，此时，若理论分布是一种连续分布（这里仅考虑连续分布的情况），则有： 

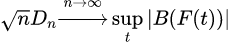
也就是说在样本点趋于无限多时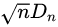，将趋向于一个Kolmogorov distribution（依分布收敛），且与F的具体形式无关。这个结果也可以称为柯尔莫戈罗夫定理。

当 n是有限的时，这个极限作为对 K的精确cdf的近似的准确性不是很好。（even when n=1000, the corresponding maximum error is about {\displaystyle 0.9\%}; this error increases to {\displaystyle 2.6\%} when {\displaystyle n=100} and to a totally unacceptable {\displaystyle 7\%} when n=10.）

 通过修正提高精度：

However, a very simple expedient of replacing x by

{\displaystyle x+{\frac {1}{6{\sqrt {n}}}}+{\frac {x-1}{4n}}}

in the argument of the Jacobi theta function reduces these errors to {\displaystyle 0.003\%}, {\displaystyle 0.027\%}, and {\displaystyle 0.27\%} respectively; such accuracy would be usually considered more than adequate for all practical applications.[5]

 拟合优度检验（goodness-of-fit test）或柯尔莫戈罗夫-斯米尔诺夫检验（Kolmogorov–Smirnov test ）可以用柯尔莫戈罗夫分布的临界值来构造。

当{\displaystyle n\to \infty }，这个检验是渐近有效的。

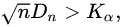 在水平 \alpha 下，若满足则拒绝零假设。其中，Kα由以下方式给出： 

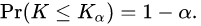
 该检验的渐进统计功效（statistical power）为1。

Test with estimated parameters

 如果从数据Xi中确定F(x)的形式或参数，则以这种方式确定的临界值无效！（来自wiki百科）

在这种情况下，可能需要蒙特卡罗方法或其他方法，但已为某些情况编制了表格。

 

查阅资料[3]可以看到，Kolmogorov测试仅用于假设分布函数完全指定的情况，也即，假设分布函数中不含有需要从样本中估出的参数。否则，该测试结果将变得保守。

 

Details for the required modifications to the test statistic and for the critical values for the normal distribution and the exponential distributionhave been published,[10] and later publications also include the Gumbel distribution.[11] The Lilliefors test represents a special case of this for the normal distribution. The logarithm transformation may help to overcome cases where the Kolmogorov test data does not seem to fit the assumption that it came from the normal distribution.

Using estimated parameters, the questions arises which estimation method should be used. Usually this would be the maximum likelihood method, but e.g. for the normal distribution MLE has a large bias error on sigma! Using a moment fit or KS minimization instead has a large impact on the critical values, and also some impact on test power. If we need to decide for Student-T data with df = 2 via KS test whether the data could be normal or not, then a ML estimate based on H0 (data is normal, so using the standard deviation for scale) would give much larger KS distance, than a fit with minimum KS. In this case we should reject H0, which is often the case with MLE, because the sample standard deviation might be very large for T-2 data, but with KS minimization we may get still a too low KS to reject H0. In the Student-T case, a modified KS test with KS estimate instead of MLE, makes the KS test indeed slightly worse. However, in other cases, such a modified KS test leads to slightly better test power.

Discrete and mixed null distribution

Two-sample Kolmogorov–Smirnov test（The Smirnov Test ）

  • Two samples. Are they coming from the same population with a specific(underlying) distribution? or the two datasets differ significantly? 两个样本集是否来自同一分布，或二者是否存在显著差异？

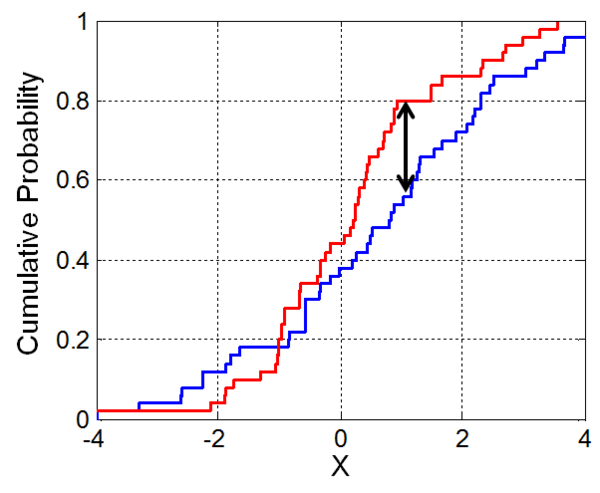
 Kolmogorov-Smirnov检验也可以用来检验两个潜在的一维概率分布是否不同。

Smirnov统计量是：

 where F_{1,n} and {\displaystyle F_{2,m}} are the empirical distribution functions of the first and the second sample respectively, and \sup  is the supremum function.

对于大样本, 零假设在水平\alpha  上被拒绝，如果：

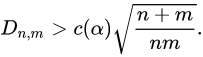
 其中 n和m分别为第一和第二样本集的大小。对于最常见的alpha级别，下表给出了 c(alpha)的值:

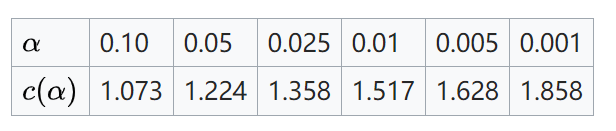
 一般可取：

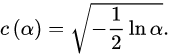
 注意，双样本测试检查两个数据样本是否来自相同的分布。这并没有指定这个常见的分布是什么(例如，它是正态分布)。同样，已经发布了临界值表。

 Kolmogorov-Smirnov检验的一个缺点是它不是很强大，因为它被设计成对两个分布函数之间所有可能的类型的差异都很敏感。[19]和[20]表明，Cucconi检验（最初提出用于同时比较位置和尺度），在比较两个分布函数时，比Kolmogorov-Smirnov检验要强大得多。

 A shortcoming of the Kolmogorov–Smirnov test is that it is not very powerful because it is devised to be sensitive against all possible types of differences between two distribution functions. [19] and [20] showed evidence that the Cucconi test, originally proposed for simultaneously comparing location and scale, is much more powerful than the Kolmogorov–Smirnov test when comparing two distribution functions.

The Kolmogorov–Smirnov statistic in more than one dimension

 

 

 参考：

[1] https://blog.csdn.net/qq_41679006/article/details/80977113

[2] https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test

[3] Conover, W. J., & Conover, W. J. (1980). Practical nonparametric statistics.

 

posted on 2019-09-23 14:32  那抹阳光1994  阅读(43248)  评论(0)  编辑  收藏  举报

导航