计算频响函数和相干函数
频响函数(FRF)
频率响应函数表征了测试系统对给定频率下的稳态输出与输入的关系。这个关系具体是指输出、输入幅值之比与输入频率的函数关系,和输出、输入相位差与输入频率的函数关系。这两个关系称为测试系统的频率特性。频率响应函数一般是一个复数。
频率响应函数直观地反映了测试系统对各个不同频率正弦输入信号的响应特性。通过频率响应函数可以画出反映测试系统动态特性的各种图形,简明直观。此外,很多工程中的实际系统很难确切地建立其数学模型,更不易确定其模型中的参数,因此要完整地列出其微分方程式并非易事。所以,工程上常通过实验方法,对系统施加激励,测量其响应,根据输入、输出关系可以确立对系统动态特性的认识。因而频率响应函数有着重要的实际意义。
和传递函数之间的关系
在系统传递函数 ![]() 已经知道的情况下,若系统是稳定的,令
已经知道的情况下,若系统是稳定的,令 ![]() 中
中 ![]() 的实部为零,即令
的实部为零,即令 ![]() 代入
代入![]() ,可以得到系统的频率响应函数
,可以得到系统的频率响应函数![]() 。
。
若在![]() 时刻将输入信号接人定常线性系统,令
时刻将输入信号接人定常线性系统,令![]() 代入拉普拉斯变换中,实际上是将拉普拉斯变换变成傅里叶变换。又由于系统的初始条件为零,因此系统的频率响应函数
代入拉普拉斯变换中,实际上是将拉普拉斯变换变成傅里叶变换。又由于系统的初始条件为零,因此系统的频率响应函数![]() 就成为输出
就成为输出![]() 、输入
、输入![]() 的傅里叶变换
的傅里叶变换![]() 之比,即
之比,即![]()
上式告诉我们,在测得输出![]() 和输入
和输入![]() 后,由其傅里叶变换
后,由其傅里叶变换![]() 可求得频率响应函数
可求得频率响应函数![]() 。
。
意义
根据定常线性系统的频率保持性,系统在简谐信号 ![]() 的激励下,所产生的稳态输出也是简谐信号)
的激励下,所产生的稳态输出也是简谐信号)![]() 。此时输入和输出虽为同频率的简谐信号,但两者的幅值并不一样,其幅值比
。此时输入和输出虽为同频率的简谐信号,但两者的幅值并不一样,其幅值比![]() 随频率
随频率![]() 而变,是
而变,是![]() 的函数。相位差
的函数。相位差![]() 也是频率
也是频率 ![]() 的函数。
的函数。
可以证明,定常线性系统在简谐信号的激励下,其稳态输出信号和输入信号的幅值比就是该系统的幅频特性,即![]() ;稳态输出对输入的相位差就是该系统的相频特性,即
;稳态输出对输入的相位差就是该系统的相频特性,即![]() 。两者统称为系统的频率特性。因此,系统的频率特性就是系统在简谐信号激励下,其稳态输出对输入的幅值比、相位差随激励频率
。两者统称为系统的频率特性。因此,系统的频率特性就是系统在简谐信号激励下,其稳态输出对输入的幅值比、相位差随激励频率![]() 变化的特性。
变化的特性。
图形表示
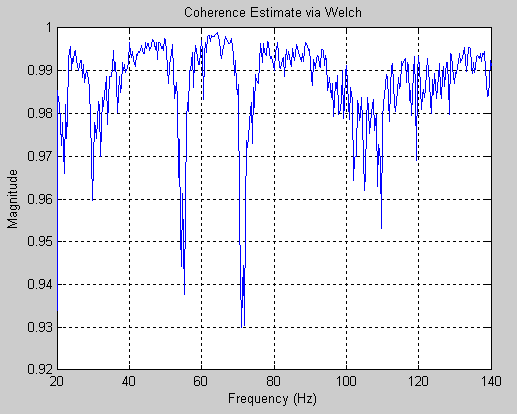
相干函数
MATLAB计算
% https://www.mathworks.com/help/signal/ref/tfestimate.html % [txy,f] = tfestimate(x,y,window,noverlap,f,fs) tfestimate(ch1,ch2,hanning(1024),1024/2,[],Fs); % 计算传递函数 % [Txy,f] = tfestimate(ch1,ch2,hanning(1024),1024/2,[],Fs); % plot(f,mag2db(abs(Txy))) xlim([20 140])

% https://www.mathworks.com/help/signal/ref/mscohere.html % [cxy,f] = mscohere(x,y,window,noverlap,f,fs) mscohere(ch1, ch2, hanning(1024),1024/2, [], Fs) % [cxy,f] = mscohere(ch1, ch2, hanning(1024),1024/2, [], Fs); % plot(f, cxy) xlim([20 140])
posted on 2019-06-23 16:41 那抹阳光1994 阅读(11850) 评论(0) 编辑 收藏 举报




