如何理解K-L散度（相对熵）

K-L散度

Kullback-Leibler Divergence，即K-L散度，是一种量化两种概率分布P和Q之间差异的方式，又叫相对熵。

在概率学和统计学上，我们经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息。

K-L散度定义见文末附录1。另外在附录5中解释了为什么在深度学习中，训练模型时使用的是Cross Entropy 而非K-L Divergence。

我们从下面这个问题出发思考K-L散度。

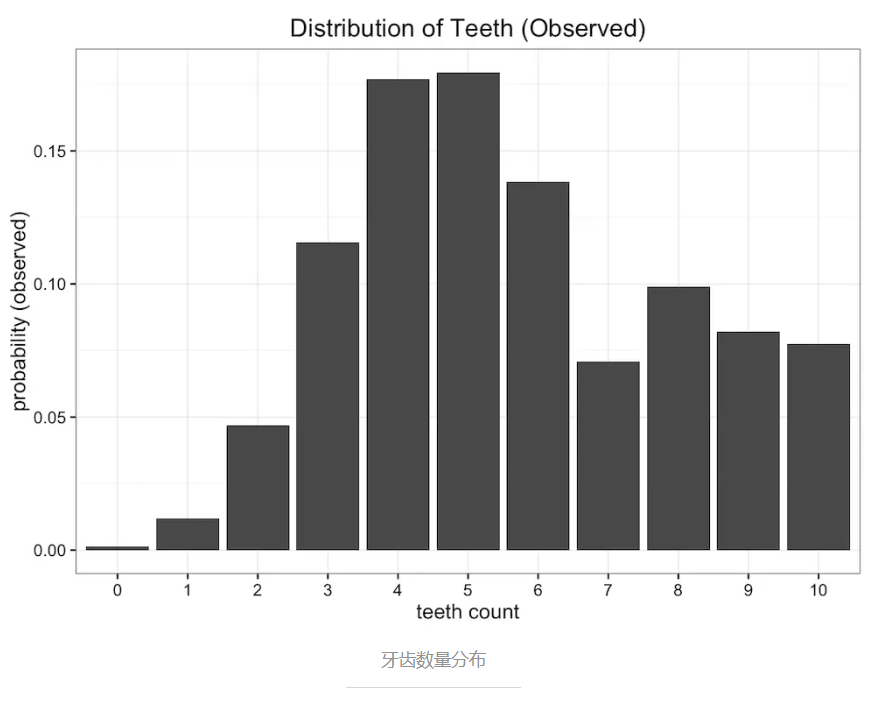
假设我们是一群太空科学家，经过遥远的旅行，来到了一颗新发现的星球。在这个星球上，生存着一种长有牙齿的蠕虫，引起了我们的研究兴趣。我们发现这种蠕虫生有10颗牙齿，但是因为不注意口腔卫生，又喜欢嚼东西，许多蠕虫会掉牙。收集大量样本之后，我们得到关于蠕虫牙齿数量的经验分布，如下图所示

这些数据很有价值，但是也有点问题。我们距离地球🌍太远了，把这些概率分布数据发送回地球过于昂贵。还好我们是一群聪明的科学家，用一个只有一两个参数的简单模型来近似原始数据会减小数据传送量。最简单的近似模型是均分布，因为蠕虫牙齿不会超过10颗，所以有11个可能值，那蠕虫的牙齿数量概率都为 1/11。分布图如下：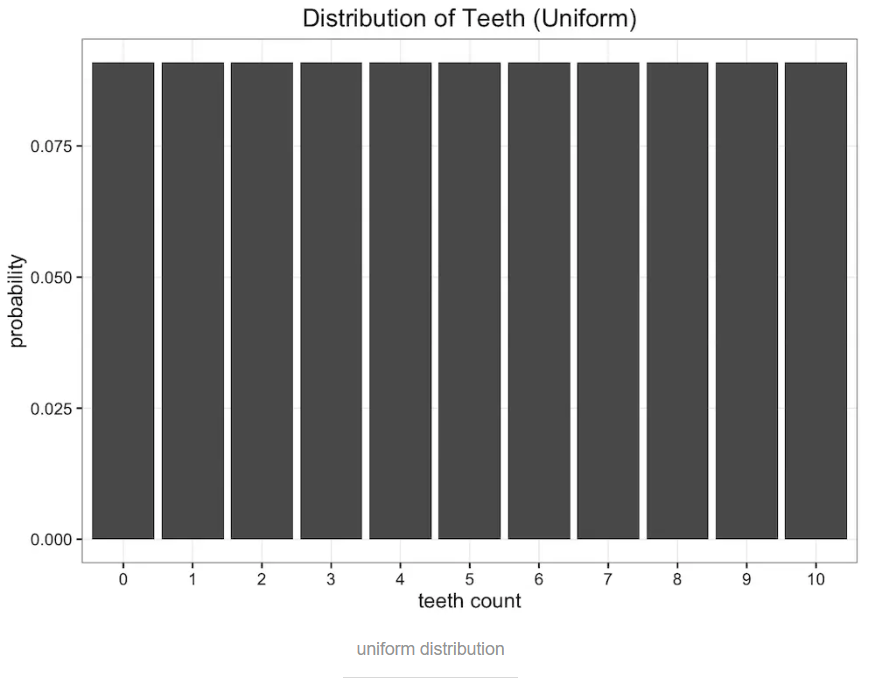

显然我们的原始数据并非均分布的，但也不是我们已知的分布，至少不是常见的分布。作为备选，我们想到的另一种简单模型是二项式分布binomial distribution。蠕虫嘴里面共有n=10个牙槽，每个牙槽出现牙齿与否为独立事件，且概率均为p。则蠕虫牙齿数量即为期望值E[x]=n*p，真实期望值即为观察数据的平均值，比如说5.7，则p=0.57，得到如下图所示的二项式分布：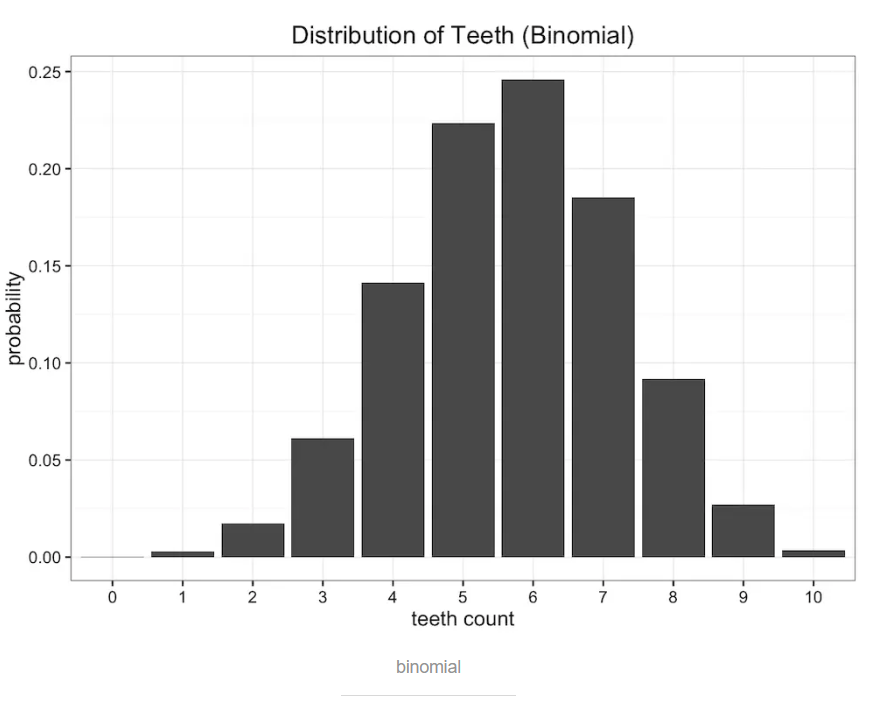

对比一下原始数据，可以看出均分布和二项分布都不能完全描述原始分布。

可是，我们不禁要问，哪一种分布更加接近原始分布呢？
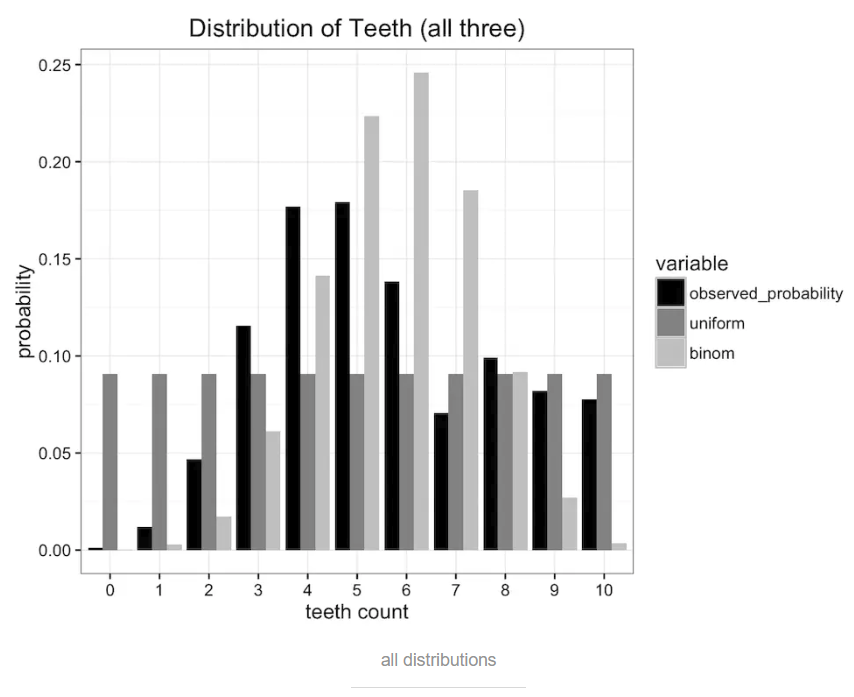
已经有许多度量误差的方式存在，但是我们所要考虑的是减小发送的信息量。上面讨论的均分布和二项式分布都把问题规约到只需要两个参数，牙齿数量和概率值（均分布只需要牙齿数量即可）。那么哪个分布保留了更多的原始数据分布的信息呢？这个时候就需要K-L散度登场了。

数据的熵

K-L散度源于信息论。信息论主要研究如何量化数据中的信息。最重要的信息度量单位是熵Entropy，一般用H表示。分布的熵的公式如下：

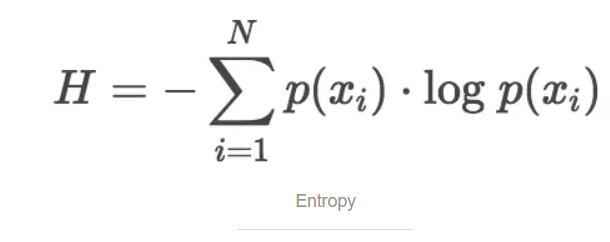
可是熵值并没有给出压缩数据到最小熵值的方法，即如何编码数据才能达到最优（存储空间最优）。优化信息编码是一个非常有意思的主题，但并不是理解K-L散度所必须的。熵的主要作用是告诉我们最优编码信息方案的理论下界（存储空间），以及度量数据的信息量的一种方式。理解了熵，我们就知道有多少信息蕴含在数据之中，现在我们就可以计算当我们用一个带参数的概率分布来近似替代原始数据分布的时候，到底损失了多少信息。请继续看下节内容。↓↓↓

K-L散度度量信息损失

只需要稍加修改熵H的计算公式就能得到K-L散度的计算公式。设p为观察得到的概率分布，q为另一分布来近似p，则p、q的K-L散度为：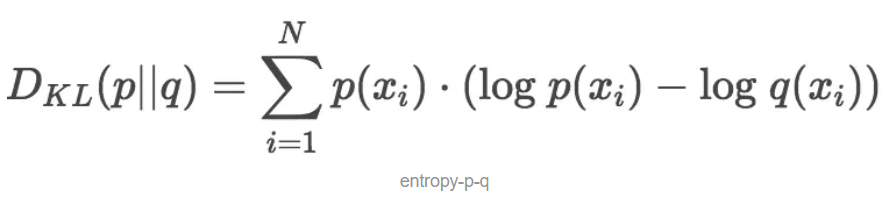

显然，根据上面的公式，K-L散度其实是数据的原始分布p和近似分布q之间的对数差值的期望。如果继续用2为底的对数计算，则K-L散度值表示信息损失的二进制位数。下面公式以期望表达K-L散度：

一般，K-L散度以下面的书写方式更常见：

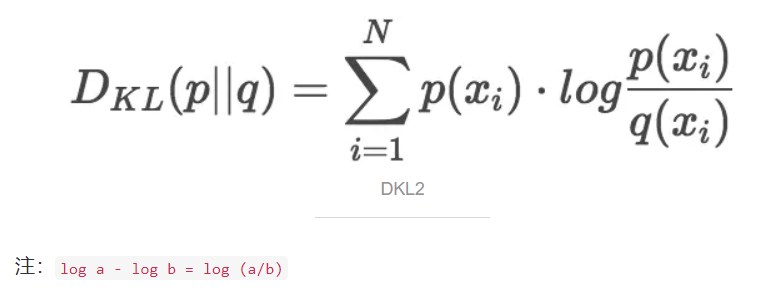
OK，现在我们知道当用一个分布来近似另一个分布时如何计算信息损失量了。接下来，让我们重新回到最开始的蠕虫牙齿数量概率分布的问题。

首先是用均分布来近似原始分布的K-L散度：

接下来计算用二项式分布近似原始分布的K-L散度：

通过上面的计算可以看出，使用均分布近似原始分布的信息损失要比用二项式分布近似小。所以，如果要从均分布和二项式分布中选择一个的话，均分布更好些。

散度并非距离

很自然地，一些同学把K-L散度看作是不同分布之间距离的度量。这是不对的，因为从K-L散度的计算公式就可以看出它不符合对称性（距离度量应该满足对称性）。如果用我们上面观察的数据分布来近似二项式分布，得到如下结果：

所以，Dkl (Observed || Binomial) != Dkl (Binomial || Observed)。也就是说，用p近似q和用q近似p，二者所损失的信息并不是一样的。

使用K-L散度优化模型

前面使用的二项式分布的参数是概率 p=0.57，是原始数据的均值。p的值域在 [0, 1] 之间，我们要选择一个p值，建立二项式分布，目的是最小化近似误差，即K-L散度。那么0.57是最优的吗？

下图是原始数据分布和二项式分布的K-L散度变化随二项式分布参数p变化情况：

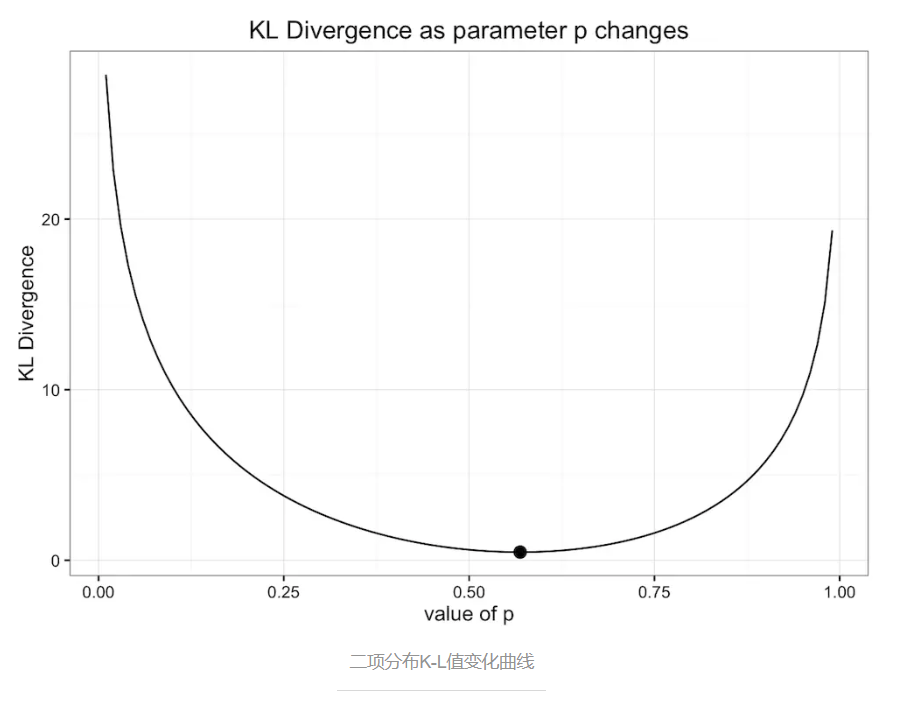
通过上面的曲线图可以看出，K-L散度值在圆点处最小，即p=0.57。所以我们之前的二项式分布模型已经是最优的二项式模型了。注意，我已经说了，是二项式模型，这里只限定在二项式模型范围内。

前面只考虑了均分布模型和二项式分布模型，接下来我们考虑另外一种模型来近似原始数据。首先把原始数据分成两部分，1）0-5颗牙齿的概率和 2）6-10颗牙齿的概率。概率值如下：

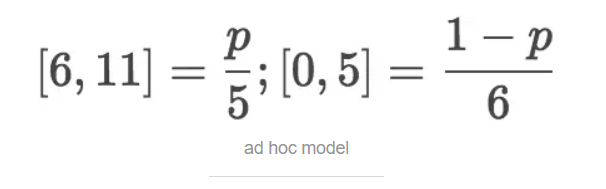
即，一只蠕虫的牙齿数量x=i的概率为p/5; x=j的概率为(1-p) / 6，i=0,1,2,3,4,5; j=6,7,8,9,10。

Aha，我们自己建立了一个新的（奇怪的）模型来近似原始的分布，模型只有一个参数p，像前面那样优化二项式分布的时候所做的一样，让我们画出K-L散度值随p变化的情况：

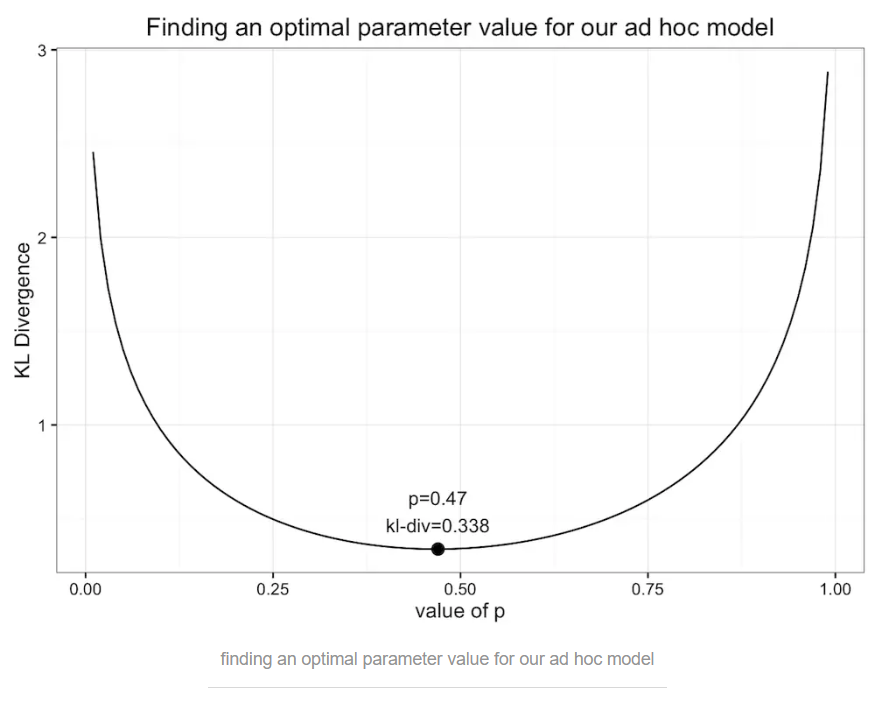
当p=0.47时，K-L值取最小值0.338。似曾相识吗？对，这个值和使用均分布的K-L散度值是一样的（这并不能说明什么）！下面我们继续画出这个奇怪模型的概率分布图，看起来确实和均分布的概率分布图相似：

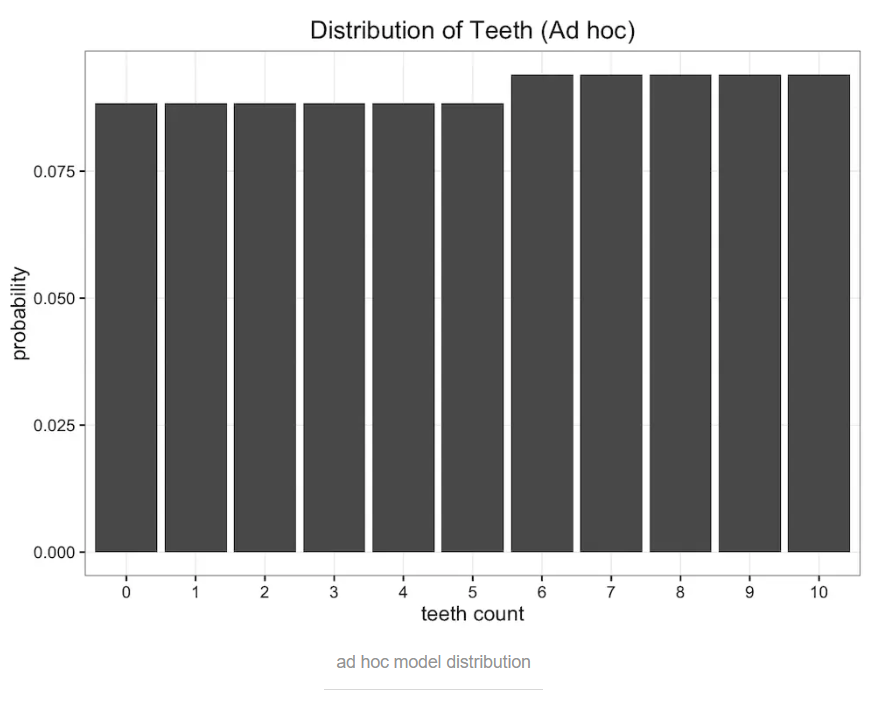
我们自己都说了，这是个奇怪的模型，在K-L值相同的情况下，更倾向于使用更常见的、更简单的均分布模型。

回头看，我们在这一小节中使用K-L散度作为目标方程，分别找到了二项式分布模型的参数p=0.57和上面这个随手建立的模型的参数p=0.47。是的，这就是本节的重点：使用K-L散度作为目标方程来优化模型。当然，本节中的模型都只有一个参数，也可以拓展到有更多参数的高维模型中。

变分自编码器VAEs和变分贝叶斯法

如果你熟悉神经网络，你可能已经猜到我们接下来要学习的内容。除去神经网络结构的细节信息不谈，整个神经网络模型其实是在构造一个参数数量巨大的函数（百万级，甚至更多），不妨记为f(x)，通过设定目标函数，可以训练神经网络逼近非常复杂的真实函数g(x)。训练的关键是要设定目标函数，反馈给神经网络当前的表现如何。训练过程就是不断减小目标函数值的过程。

我们已经知道K-L散度用来度量在逼近一个分布时的信息损失量。K-L散度能够赋予神经网络近似表达非常复杂数据分布的能力。变分自编码器（Variational Autoencoders，VAEs）是一种能够学习最佳近似数据集信息（分布）的常用方法，Tutorial on Variational Autoencoders 2016是一篇关于VAEs的非常不错的教程，里面讲述了如何构建VAE的细节。 What are Variational Autoencoders? A simple explanation简单介绍了VAEs，Building Autoencoders in Keras介绍了如何利用Keras库实现几种自编码器。

变分贝叶斯方法（Variational Bayesian Methods）是一种更常见的方法。这篇文章介绍了强大的蒙特卡洛模拟方法能够解决很多概率问题。蒙特卡洛模拟能够帮助解决许多贝叶斯推理问题中的棘手积分问题，尽管计算开销很大。包括VAE在内的变分贝叶斯方法，都能用K-L散度生成优化的近似分布，这种方法对棘手积分问题能进行更高效的推理。更多变分推理（Variational Inference）的知识可以访问Edward library for python。

附录

K-L 散度的定义

计算K-L的注意事项

信息熵、交叉熵、相对熵

信息熵，即熵，香浓熵。编码方案完美时，最短平均编码长度。
交叉熵，cross-entropy。编码方案不一定完美时（由于对概率分布的估计不一定正确），平均编码长度。是神经网络常用的损失函数。
相对熵，即K-L散度，relative entropy。编码方案不一定完美时，平均编码长度相对于最小值的增加值。
更详细对比，见知乎如何通俗的解释交叉熵与相对熵?

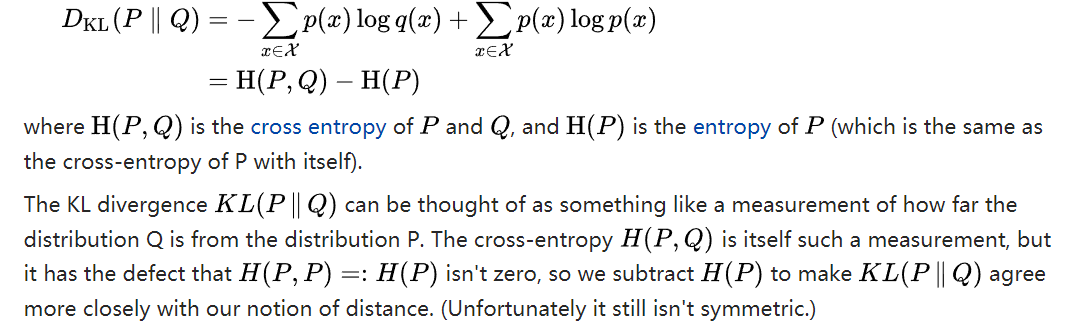
KL散度可以看做是分布Q和分布P之间远近的一种度量。而交叉熵本身就是这样的一种度量，缺点是自己与自己的交叉熵不为零（等于熵值），因此我们将交叉熵减去熵值，使KL散度更接近距离的定义（不幸的是它依然是不对称的）。

为什么在神经网络中使用交叉熵损失函数，而不是K-L散度？

K-L散度=交叉熵-熵，即 DKL( p||q )=H(p,q)−H(p)。

在神经网络所涉及到的范围内，H(p)不变，则DKL( p||q )等价H(p,q)。

译自：Kullback-Leibler Divergence Explained
作者：Will Kurt
If you enjoyed this post please subscribe to keep up to date and follow @willkurt!
If you enjoyed this writing and also like programming languages, you might like the book on Haskell I just finished due in print July 2017 (though nearly all the content is available online today).

Matlab 代码实现

Kullback-Leibler divergence、Symmetric variant of the Kullback-Leibler divergence、Jensen-Shannon divergence的计算：

function KL = kldiv(varValue,pVect1,pVect2,varargin)
%KLDIV Kullback-Leibler or Jensen-Shannon divergence between two distributions.
%   KLDIV(X,P1,P2) returns the Kullback-Leibler divergence between two
%   distributions specified over the M variable values in vector X.  P1 is a
%   length-M vector of probabilities representing distribution 1, and P2 is a
%   length-M vector of probabilities representing distribution 2.  Thus, the
%   probability of value X(i) is P1(i) for distribution 1 and P2(i) for
%   distribution 2.  The Kullback-Leibler divergence is given by:
%
%       KL(P1(x),P2(x)) = sum[P1(x).log(P1(x)/P2(x))]
%
%   If X contains duplicate values, there will be an warning message, and these
%   values will be treated as distinct values.  (I.e., the actual values do
%   not enter into the computation, but the probabilities for the two
%   duplicate values will be considered as probabilities corresponding to
%   two unique values.)  The elements of probability vectors P1 and P2 must 
%   each sum to 1 +/- .00001.
%
%   A "log of zero" warning will be thrown for zero-valued probabilities.
%   Handle this however you wish.  Adding 'eps' or some other small value 
%   to all probabilities seems reasonable.  (Renormalize if necessary.)
%
%   KLDIV(X,P1,P2,'sym') returns a symmetric variant of the Kullback-Leibler
%   divergence, given by [KL(P1,P2)+KL(P2,P1)]/2.  See Johnson and Sinanovic
%   (2001).
%
%   KLDIV(X,P1,P2,'js') returns the Jensen-Shannon divergence, given by
%   [KL(P1,Q)+KL(P2,Q)]/2, where Q = (P1+P2)/2.  See the Wikipedia article
%   for "Kullback-Leibler divergence".  This is equal to 1/2 the so-called
%   "Jeffrey divergence."  See Rubner et al. (2000).
%
%   EXAMPLE:  Let the event set and probability sets be as follow:
%                X = [1 2 3 3 4]';
%                P1 = ones(5,1)/5;
%                P2 = [0 0 .5 .2 .3]' + eps;
%  
%             Note that the event set here has duplicate values (two 3's). These 
%             will be treated as DISTINCT events by KLDIV. If you want these to
%             be treated as the SAME event, you will need to collapse their
%             probabilities together before running KLDIV. One way to do this
%             is to use UNIQUE to find the set of unique events, and then
%             iterate over that set, summing probabilities for each instance of
%             each unique event.  Here, we just leave the duplicate values to be
%             treated independently (the default):
%                 KL = kldiv(X,P1,P2); 
%                 KL =  
%                      19.4899
%
%             Note also that we avoided the log-of-zero warning by adding 'eps' 
%             to all probability values in P2.  We didn't need to renormalize
%             because we're still within the sum-to-one tolerance. 
%  
%   REFERENCES:
%   1) Cover, T.M. and J.A. Thomas. "Elements of Information Theory," Wiley, 
%      1991.
%   2) Johnson, D.H. and S. Sinanovic. "Symmetrizing the Kullback-Leibler 
%      distance." IEEE Transactions on Information Theory (Submitted).
%   3) Rubner, Y., Tomasi, C., and Guibas, L. J., 2000. "The Earth Mover's 
%      distance as a metric for image retrieval." International Journal of 
%      Computer Vision, 40(2): 99-121.
%   4) Kullback-Leibler divergence. Wikipedia, The Free Encyclopedia.
%
%   See also: MUTUALINFO, ENTROPY

if ~isequal(unique(varValue),sort(varValue))
    warning('KLDIV:duplicates','X contains duplicate values. Treated as distinct values.')
end
if ~isequal(size(varValue),size(pVect1)) || ~isequal(size(varValue),size(pVect2))
    error('All inputs must have same dimension.')
end
% Check probabilities sum to 1:
if (abs(sum(pVect1) - 1) > .00001) || (abs(sum(pVect2) - 1) > .00001)
    error('Probablities don''t sum to 1.')
end

if isempty(varargin)
    varargin{1} = 'kl'; % 默认计算KL散度
    % The logarithms in these formulae are taken to base 2 if information is measured in units of bits, 
    % or to base e if information is measured in nats. 
    % Most formulas involving the Kullback–Leibler divergence hold regardless of the base of the logarithm.
    varargin{2} = '2'; % 默认以2为对数基底(information is measured in units of bits)
end

if ~isempty(varargin)
    switch varargin{2}
        case '2'
            switch varargin{1}
                case 'js'
                    logQvect = log2((pVect2+pVect1)/2);
                    KL = .5 * (sum(pVect1.*(log2(pVect1)-logQvect)) + ...
                        sum(pVect2.*(log2(pVect2)-logQvect)));

                case 'sym'
                    KL1 = sum(pVect1 .* (log2(pVect1)-log2(pVect2)));
                    KL2 = sum(pVect2 .* (log2(pVect2)-log2(pVect1)));
                    KL = (KL1+KL2)/2;
        
                case 'kl'
                    KL = sum(pVect1 .* (log2(pVect1)-log2(pVect2)));
                otherwise
                    error(['Last argument' ' "' varargin{1} '" ' 'not recognized.'])
            end
        case 'e'
            switch varargin{1}
                case 'js'
                    logQvect = log((pVect2+pVect1)/2);
                    KL = .5 * (sum(pVect1.*(log(pVect1)-logQvect)) + ...
                        sum(pVect2.*(log(pVect2)-logQvect)));
                case 'sym'
                    KL1 = sum(pVect1 .* (log(pVect1)-log(pVect2)));
                    KL2 = sum(pVect2 .* (log(pVect2)-log(pVect1)));
                    KL = (KL1+KL2)/2;
                case 'kl'
                    KL = sum(pVect1 .* (log(pVect1)-log(pVect2)));
                otherwise
                    error(['Last argument' ' "' varargin{1} '" ' 'not recognized.'])
            end
        otherwise
            error(['Last argument' ' "' varargin{2} '" ' 'not recognized.'])
     end
end

参考：https://www.jianshu.com/p/43318a3dc715

posted on 2019-04-20 16:34 那抹阳光1994 阅读(3220) 评论(1) 编辑收藏举报

刷新页面返回顶部

那抹阳光1994