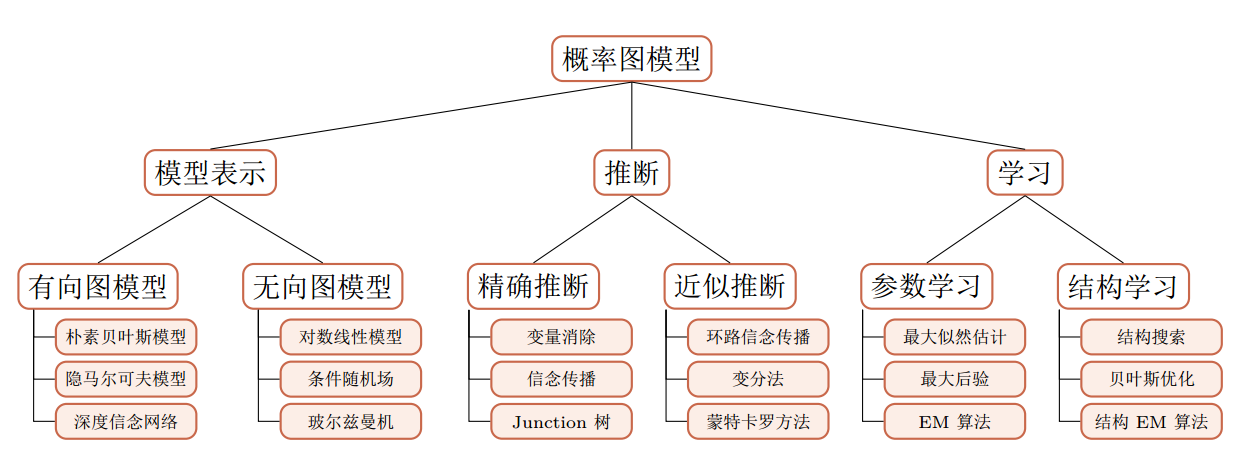
概率图模型（GM）
概率图模型
概率图模型（Probabilistic Graphical Model，PGM），简称图模型（Graphical Model， GM），是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型，
从而给研究高维空间中的概率模型带来了很大的便捷性。
高维随机变量的联合概率为高维空间中的分布，一般难以直接建模。在不做任何独立性假设的条件下，模型的参数将随维度的增长呈指数级增长。
一种有效减少参数量的方法是独立性假设。如果某些变量之间存在条件独立性，其参数数量就可以大幅减少。因此，如何描述多元随机变量之间的条件独立关系成为高维空间概率模型构建的关键。
当概率模型中的变量数量比较多时，其条件依赖关系也比较复杂。我们可以使用图结构的方式将概率模型可视化，以一种直观、简单的方式描述随机变量之间的条件独立性的性质，
并可以将一个复杂的联合概率模型分解为一些简单条件概率模型的组合。
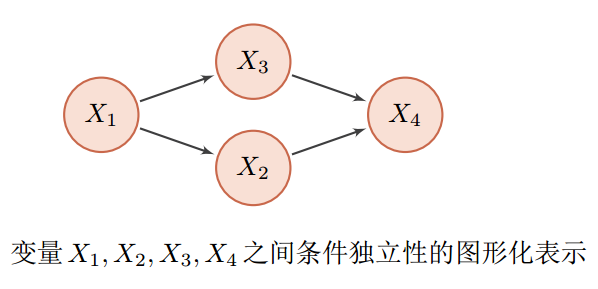图中给出了4个变量之间的条件独立性的图形化描述。图中每个节点表示一个变量，每条连边变量之间的依赖关系。对于一个非全连接的图，都存在一个或多个条件独立性假设，可以根据条件独立性将联合概率分布进行分解，表示为一组局部条件概率分布的乘积。联合概率分布可表示为：
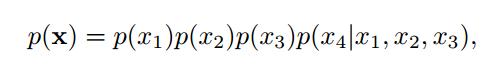
图模型的基本问题
图模型有三个基本问题：
- 1. 表示问题：对于一个概率模型，如何通过图结构来描述变量之间的依赖关系。
- 2. 推断问题：在已知部分变量时，计算其它变量的后验概率分布。
- 3. 学习问题：图模型的学习包括图结构的学习和参数的学习。
表示问题
如何通过图结构来描述变量之间的依赖关系？
图由一组节点和节点之间的边组成。在概率图模型中，每个节点都表示一个随机变量（或一组随机变量）， 边表示这些随机变量之间的概率依赖关系。
常见的概率图模型可以分为两类：
- 有向图模型
- 无向图模型
有向图模型的图结构为有向非循环图，如果两个节点之间有连边，表示对于的两个变量为因果关系。
无向图模型使用无向图来描述变量之间的关系。每条边代表两个变量之间有概率依赖关系，但是并不一定是因果关系。
带阴影的节点表示可观测到的变量，不带阴影的节点表示隐变量，连边表示两变量间的条件依赖关系 。
有向图模型
有向图模型（Directed Graphical model），也称为贝叶斯网络（BayesianNetwork），或信念网络（Belief Network， BN），是指用有向图来表示概率分布的图模型。
条件独立性：在贝叶斯网络中，如果两个节点是直接连接的，它们肯定是非条件独立的，是直接因果关系。父节点是“因”，子节点是“果”。
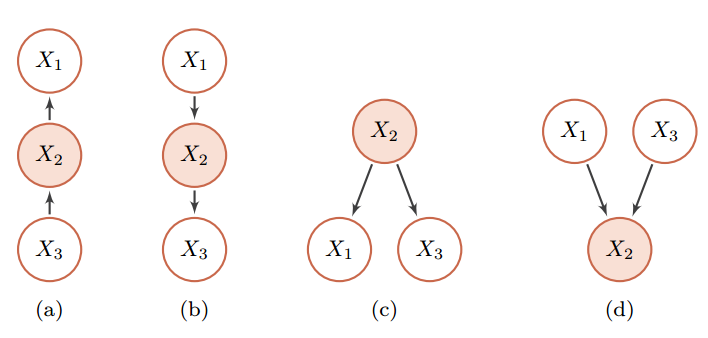
如果两个节点不是直接连接的，但是它们之间有一条经过其它节点的路径来连接，那么这两个节点之间的条件独立性就比较复杂。
- 间接因果
- 间接果因
- 共因关系
- 共果关系
常见的有向图模型 ：
- sigmoid 信念网络
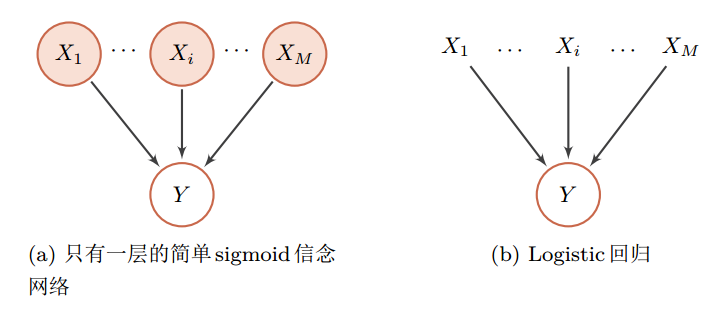
- 朴素贝叶斯分类器
- 隐马尔可夫模型
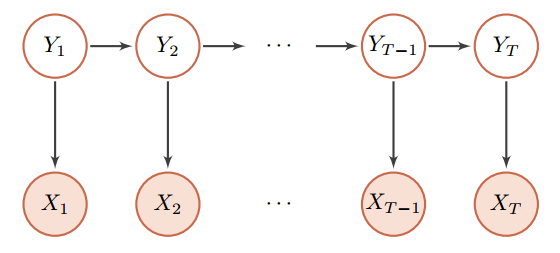
无向图模型
无向图模型，也称为马尔可夫随机场（Markov Random Field， MRF）或马尔可夫网络（Markov Network），是一类用无向图来描述一组具有局部马尔可夫性质的随机向量 X的联合概率分布的模型。
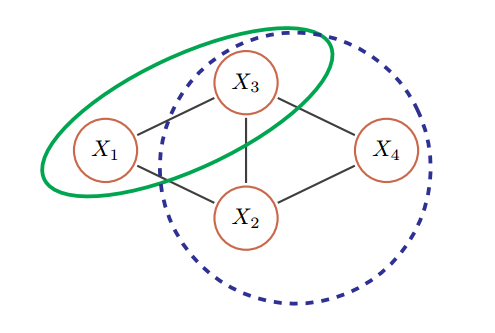
无向图模型中的团和最大团
常见的无向图模型 ：
- 对数线性模型（最大熵模型 ）
- 条件随机场
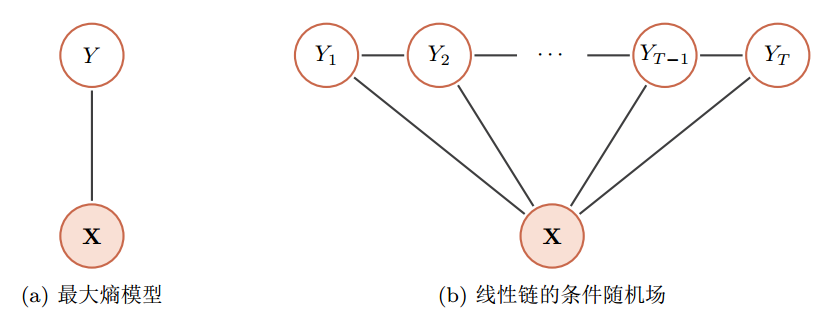
有向图和无向图之间的转换
无向图模型可以表示有向图模型无法表示的一些依赖关系，比如循环依赖；
但它不能表示有向图模型能够表示的某些关系，比如因果关系。
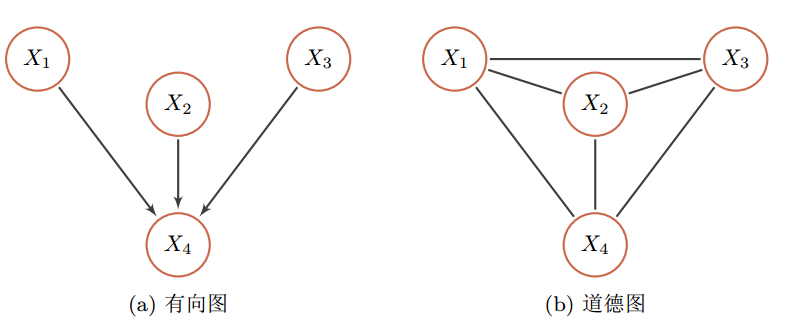
具有共果关系的有向图的道德化示例
推断问题
推断问题：在已知部分变量时，计算其它变量的后验概率分布。
在图模型中， 推断（inference）是指在观测到部分变量e = {e1, e2, · · · , em}时，计算其它变量的某个子集 q = {q1, q2, · · · , qn}的后验概率 p(q|e)。
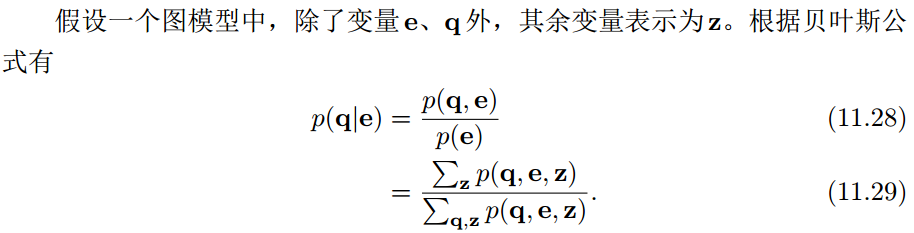因此，图模型的推断问题可以转换为求任意一个变量子集的边际概率分布问题。
在图模型中，常用的推断方法可以分为：
- 精确推断
- 近似推断
精确推断
变量消除法
信念传播算法
近似推断
在实际应用中，精确推断一般用于结构比较简单的推断问题。当图模型的结构比较复杂时，精确推断的计算开销会比较大。此外，如果图模型中的变量是连续的，并且其积分函数没有闭型（closed-form）解时，也无法使用精确推断。因此，在很多情况下也常常采用近似的方法来进行推断。
近似推断（Approximate Inference）主要有以下三种方法：
1. 环路信念传播
当图模型中存在环路时，使用和积算法时，消息会在环路中一直传递，可能收敛或不收敛。 环路信念传播（Loopy Belief Propagation，LBP）是在具有环路的图上依然使用和积算法，即使得到不精确解，在某些任务上也可以近似精确解。
2. 变分法
图模型中有些变量的局部条件分布可能非常复杂，或其积分无法计算。 变分法（Variational Method）是引入一个变分分布（通常是比较简单的分布）来近似这些条件概率，然后通过迭代的方法进行计算。首先是更新变分分布的参数来最小化变分分布和真实分布的差异（比如交叉熵或 KL距离），然后再根据变分分布来进行推断。
3. 采样法
采样法（Sampling Method）是通过模拟的方式来采集符合某个分布 p(x)的一些样本，并通过这些样本来估计和这个分布有关的运算，比如期望等。
采样法（Sampling Method），也叫蒙特卡罗方法（Monte Carlo Method）或统计模拟方法
基于采样法的近似推断
- 蒙特卡罗方法
- 拒绝采样
- 重要性采样
- 马尔可夫链蒙特卡罗方法（MCMC）
- Metropolis-Hastings 算法
- Metropolis 算法
- 吉布斯采样
学习问题
图模型的学习可以分为两部分：
一是网络结构学习，即寻找最优的网络结构。网络结构学习一般比较困难，一般是由领域专家来构建。
二是网络参数估计，即已知网络结构，估计每个条件概率分布的参数。
不含隐变量的参数估计
如果图模型中不包含隐变量，即所有变量都是可观测的，那么网络参数一般可以直接通过最大似然来进行估计。
含隐变量的参数估计
如果图模型中包含隐变量，即有部分变量是不可观测的，就需要用 EM算法进行参数估计。
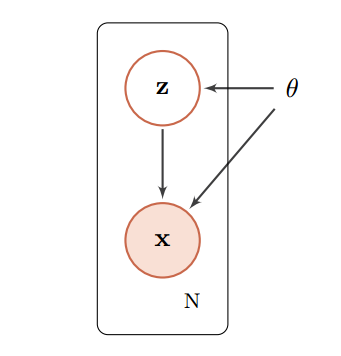
带隐变量的贝叶斯网络。图中的矩形表示其中的变量重复 N 次。
EM 算法是含隐变量图模型的常用参数估计方法，通过迭代的方法来最大化边际似然。 EM算法具体分为两个步骤： E步和 M步。这两步不断重复，直到收敛到某个局部最优解。
EM算法的应用例子：高斯混合模型。
高斯混合模型（Gaussian Mixture Model， GMM）是由多个高斯分布组成的模型，其密度函数为多个高斯密度函数的加权组合。
概率图模型提供了一个用图形来描述概率模型的框架，这种可视化方法使我们可以更加容易地理解复杂模型的内在性质。
目前，概率图模型已经是一个非常庞大的研究领域，涉及众多的模型和算法。很多机器学习模型也都可以用概率图模型来描述。
图模型与神经网络的关系
1. 图模型和神经网络有着类似的网络结构，但两者也有很大的不同。
图模型的节点是随机变量，其图结构的主要功能是用来描述变量之间的依赖关系，一般是稀疏连接。使用图模型的好处是可以有效进行统计推断。
而神经网络中的节点是神经元，是一个计算节点。如果将神经网络中每个神经元看做是一个二值随机变量，那神经网络就变成一个 sigmoid信念网络。
2. 图模型中的每个变量一般有着明确的解释，变量之间依赖关系一般是人工来定义。而神经网络中的单个神经元则没有直观的解释。
3. 神经网络是判别模型，直接用来分类。而图模型不但可以是判别模型，也可以是生成模型。生成模型不但可以用来生成样本，也可以通过贝叶斯公式用来做分类。
4. 图模型的参数学习的目标函数为似然函数或条件似然函数，若包含隐变量则通常通过 EM算法来求解。而神经网络参数学习的目标为交叉熵或平方误差等损失函数。
目前，神经网络和概率图模型的结合越来越进行紧密。
一方面我们可以利用神经网络强大的表示能力来建模图模型中的推断问题（比如变分自编码器），生成问题（比如生成对抗网络），或势能函数（比如LSTM+CRF模型 [Lample et al., 2016, Ma and Hovy, 2016]）；
另一方面可以利用图模型的算法来解决复杂结构神经网络中的学习和推断问题，比如图结构神经网络（Graph Neural Network） [Gilmer et al., 2017, Li et al., 2015, Scarselli et al., 2009]和结构化注意力 [Kim et al., 2017]。
