PM、GAN、InfoGAN、对抗自编码模型对比
本文源自知乎,仅作为个人学习使用。
链接:https://zhuanlan.zhihu.com/p/27159510
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
前段时间我受极视角邀请,在斗鱼上直播分享有关GAN的话题。考虑到现在网上关于GAN的文章、视频都已经非常多了,所以我就故意选择了一个之前没有什么人讲过的主题:LSTM之父Schmidhuber与GAN之间的恩怨纠葛。其实这件事在英文网上传播得还挺广,而且除了八卦之外也有一些严肃的学术讨论,可惜相关的中文信息寥寥,不过这样倒正好给我一个机会来给大家介绍一些新内容。
其实相比视频直播我还是更喜欢写成文章的形式,因为后者更适合深入理解和收藏回顾。所以为了方便错过直播或者不习惯看视频的朋友,我对当晚直播内容进行了文字整理,全文分为以下四个部分:
- 八卦Schmidhuber与GAN之间的恩怨
- 讲解Schmidhuber在92年提出的PM模型
- 简单介绍GAN、InfoGAN、对抗自编码器三个模型
- 对比以上四个模型之间的异同
如果选择看直播回放,可以到百度云下载。
链接:http://pan.baidu.com/s/1skUZidn
密码:200j
一、双雄捉对
2016年12月,NIPS大会,Ian Goodfellow的GAN Tutorial上,发生了尴尬的一幕。

正当Goodfellow讲到GAN与其他模型的比较时,台下一位神秘人物站起来打断了演讲,自顾自地说了一大通话(视频片段在此)


本文八卦的正是这位大佬跟Goodfellow在GAN上的争论,但其实这早就不是Schmidhuber第一次开炮怼人了。再往前2015年的时候,我们熟知的三巨头Hinton、Lecun、Bengio在Nature上发表了一篇《Deep Learning》综述之后,Schmidhuber就站出来指责他们行文偏颇,认为他们没有重视自己做出的很多贡献,觉得自己没有得到应有的荣誉,而Lecun之后也发文霸气反驳,场面十分激烈。当然这不是本文的重点,感兴趣的朋友可以进一步挖掘,下面还是继续回到NIPS演讲现场,看看Schmidhuber这回究竟又是为何开炮。
只见他站起来之后,先讲自己在1992年提出了一个叫做Predictability Minimization的模型,它如何如何,一个网络干嘛另一个网络干嘛,花了好几分钟,接着话锋一转,直问台上的Goodfellow:“你觉得我这个PM模型跟你的GAN有没有什么相似之处啊?”

似乎只是一个很正常的问题,可是Goodfellow听完后反应却很激烈。Goodfellow表示,Schmidhuber已经不是第一次问我这个问题了,之前呢我和他就已经通过邮件私下交锋了几回,所以现在的情况纯粹就是要来跟我公开当面对质,顺便浪费现场几百号人听tutorial的时间。然后你问我PM模型和GAN模型有什么相似之处,我早就公开回应过你了,不在别的地方,就在我当年的论文中,而且后来的邮件也已经把我的意思说得很清楚了,还有什么可问的呢?

确实正如Goodfellow所言,早在2014年的第一篇GAN论文中,PM已经被拿出来跟GAN进行了比较,举了三点不同之处。不过那只是论文的最终版本,而在一开始投递NIPS的初稿中并没有下面这段文字,也就是说很可能Goodfellow一开始是不知道有PM这么一个东西的。

那为什么在最终版本里又出现了PM的内容呢?原来,当年Schmidhuber就是NIPS的审稿人,而且刚好就审到了Goodfellow的论文。我们现在知道这篇论文挖了一个巨大无比的坑,引得大批人马前仆后继都来做GAN的研究,以后也应该是能写进教科书的经典工作。但就是这样牛逼的一篇论文,当年Schmidhuber居然给出了拒稿意见!当然另外两位审稿人识货,所以论文最后还是被收了。
回到正题,当时Schmidhuber在评审意见中认为,他92年提出的PM模型才是“第一个对抗网络”,而GAN跟PM的主要差别仅仅在于方向反过来了,可以把GAN名字改成“inverse PM”,即反过来的PM。按他的意思,GAN简直就是个PM的变种模型罢了。

Goodfellow当然不同意,所以就有了14年最终版本里的三点不同之处,具体细节放在最后模型比较的部分再讲。然而Schmidhuber并不接受这些说法,私下里又通过邮件跟Goodfellow进行了一番争论,还到16年的NIPS大会上打断演讲,公开较劲,就是想让对方承认PM模型的地位和贡献,可谓不依不饶。
Goodfellow也不客气,干脆在2016年的GAN Tutorial中完全移除了对PM的比较和引用。他在Quora上公开表示,“我从没有否认GAN跟另外一些模型有联系,比如NCE,但是GAN跟PM之间我真的认为没太大联系。”更有意思的是,Goodfellow还透露说,“Jürgen和我准备合写一篇paper来比较PM和GAN——如果我们能够取得一致意见的话。”想必真要写出来,背后又要经过一番激烈的争论了。
说了这么多,所谓的PM模型究竟是什么?它跟GAN究竟有多少相同多少不同?还有,这个“古老”的模型能给今天的GAN研究带来什么启发吗?大家心里肯定充满了疑问。那么八卦结束,我们现在就来走近科学,走近尘封多年的PM模型。
二、古老智慧
Predictability Minimization(可预测性最小化)模型,简称PM模型,出自1992年的论文《Learning Factorial Codes by Predictability Minimization》,Jürgen Schmidhuber是唯一的作者。对于类似我这样二零一几年才接触深度学习的人来说,它几乎就是“中古时期”的文献了。

理解PM模型,首先得从自编码器说起。大家知道机器学习分为有监督学习、无监督学习和强化学习,无监督学习中一个很重要的领域是表征学习,旨在从原始数据中学习到一个良好的表征,而自编码器就是用于表征学习的代表模型。
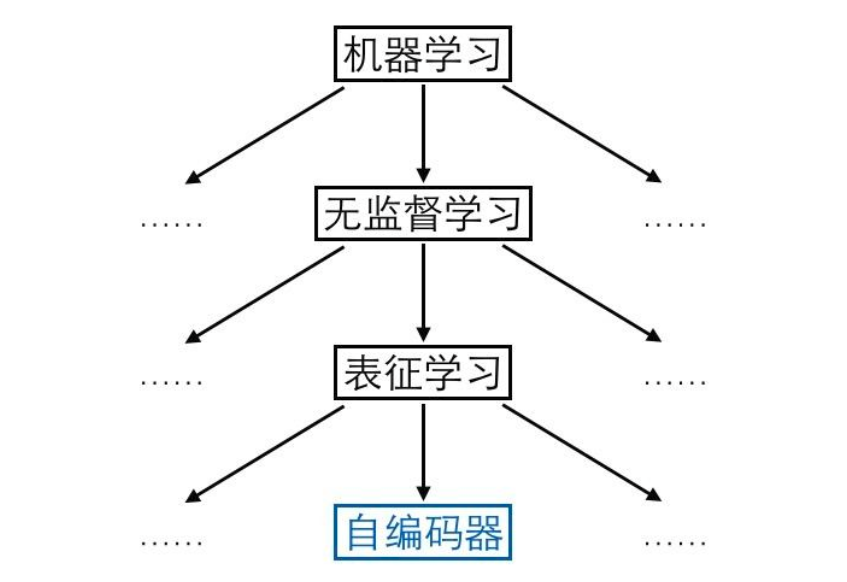
自编码器由两个模块——编码器(encoder)和解码器(decoder)组成。编码器负责输入原始样本,输出压缩编码(code);解码器负责输入编码,还原出原始样本。解码还原出来的样本跟真正的原始样本进行比较,可以计算重构误差,自编码器的训练目标就是尽可能地减少这个重构误差。
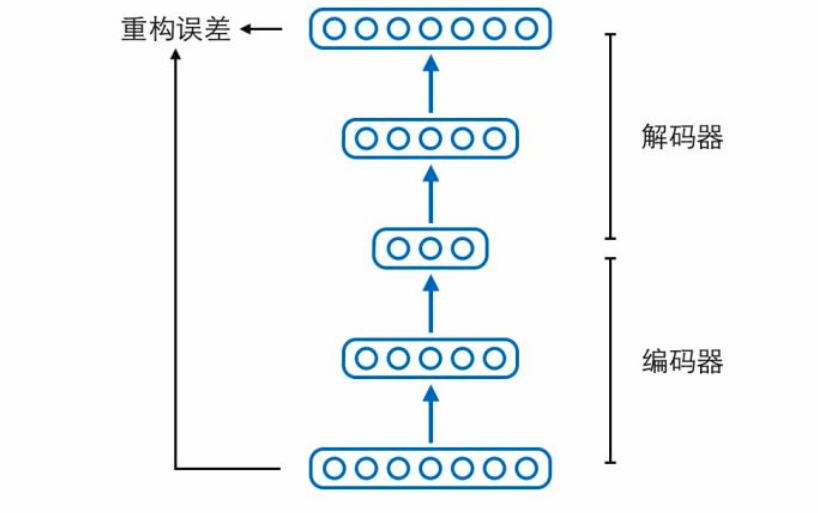
如果自编码器经过训练能够很好地重构样本,那意味着编码器和解码器中间的隐藏层节点保留了原始样本的重要信息,我们把中间这层节点构成的向量称为表征(representation)、特征(feature)或编码(code),这三个词其实可以当成同义词。
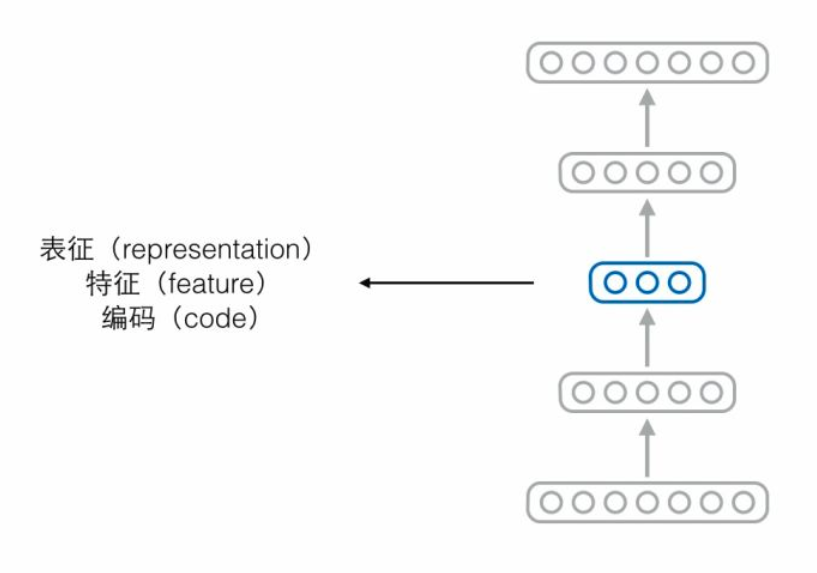
比如有人认为编码向量的各个维度代表了样本所具有的属性,而单独一个样本不应该同时具备那么多种属性,所以合理的情况是编码向量中大多数维度都是0(不激活),只有少数维度不为0(激活),此为“稀
疏”,附带稀疏要求的编码器就叫稀疏自编码器。
再比如有人认为自编码器不能死记硬背,需要在“理解”样本的基础上对样本进行编码,即便输入的时候存在一些噪声损坏了样本,自编码器也要能够还原出完好的原始样本,在此条件下编码出来的向量可能会更具语义信息,此为“降噪”,附带降噪要求的编码器就叫降噪自编码器。
除了稀疏、降噪,还有人认为编码向量的各个维度之间应该相互独立,此为“解耦”(factorial / disentangled),也是下文的重点。为了方便起见,我们考虑编码只有3个维度的情况,此时解耦在数学形式上表现
为:
(1)
其中是全部训练样本而非单个样本,
对应编码的第
个维度。为方便起见,下文省略
。
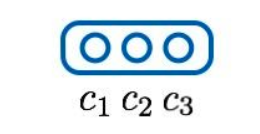
直观上说,一个解耦的编码(factorial code)把原本混杂在样本中的各个独立要素拆解开来,用一个个维度分别表示,就像人类通过拆解独立要素来认知复杂事物一样,所以可以认为它是一个“好”的表征。
现在问题来了,我们可以通过L1正则化给来自编码器提出稀疏的要求,可以通过输入加噪来给自编码器提出降噪的要求,那要怎么给自编码器提出解耦的要求呢?当年Schmidhuber就想到了非常聪明的方法。
首先,上面公式(1)可以换一个表述,改写成三个条件独立表达式:
(2a)
(2b)
(2c)
直观上可以把这组式子解释为,一个编码维度旁边的“兄弟维度”对于预测该维度没有额外帮助,比如说知道了和
并不能帮助我们将
猜得更准。
接着,使用三个预测器网络把上述逻辑具体化,其中预测器1负责预测维度1,输入维度2和3,以此类推,数学形式如下:
(3a)
(3b)
网络形式如下:
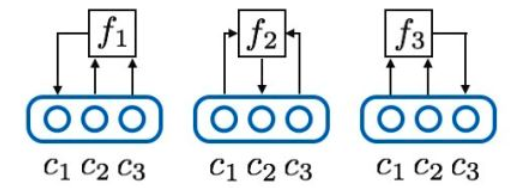
(4a)
(4b)
(4c)
按Schmidhuber的思想,上述loss体现了各个编码维度的解耦程度。怎么说呢?以预测器1为例,如果和
很有关系,甚至极端情况下
恒等于
,那么
就能够猜得很准。此时
关于
条件不独立,很有可预测性(predictability),我们就认为
没能从
中解耦。
这显然不是想要的局面。为了将与
解耦,编码器就得尽可能让预测器猜不中,loss上体现为:
(5)
预测器1想要猜中维度1,而编码器想要让它猜不中,loss函数刚好相反,,两者之间存在对抗。如果编码器赢了,就代表与
关系不大,成功解耦。
接下来考虑上所有维度,再把公式写得通用一点。每个预测器试图猜中它所负责的编码维度,体现了编码的可预测性,其loss为:
(6)
编码器试图让所有预测器都猜不中,试图最小化可预测性,其loss与预测器相反:
(7)
如果编码器赢了,就解耦了编码向量的各个维度。至此,读者就可以理解Schmidhuber论文标题的含义了:Learning Factorial Codes by Predictability Minimization,通过最小化可预测性,来学习一个解耦的编码表示。
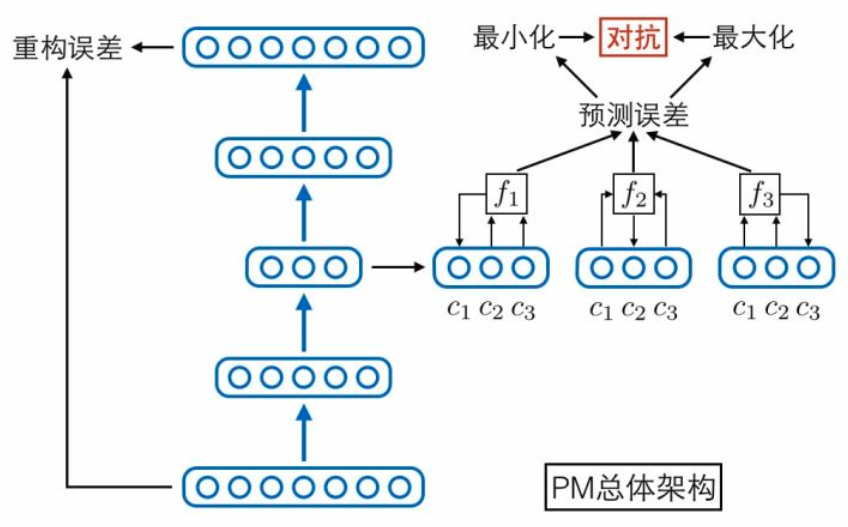
当然,除了上述两个相互对抗可预测性loss,别忘了还有个自编码器本身的重构误差loss,它能够保证编码中尽可能保留了原始输入样本的重要信息。论文中其实还有其他loss,但不是重点,感兴趣的人可以去读原论文。将上述网络模块与loss函数全部集中在一起,就形成了PM模型的总体架构图,我们用这张图作为第二部分的总结:
三、三个后辈
知道了PM是啥,接下来的问题就是它跟GAN究竟有多相似,但实际上GAN的两个后续变种——InfoGAN、对抗自编码器反而跟PM更像,所以第三部分先简单介绍这三个模型,再在第四部分跟PM进行综合比较。相关论文如下:
Generative Adversarial NetsInfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
Adversarial Autoencoders
第一个模型是大家已经很熟悉的GAN,分为生成器(generator)和判别器(discriminator)两个模块。生成器输入一个随机编码向量,输出一个复杂样本(如图片);判别器输入一个复杂样本,输出一个概率表示该样本是真实样本还是生成器产生的假样本。判别器的目标是区分真假样本,生成器的目标是让判别器区分不出真假样本,两者目标相反,存在对抗。
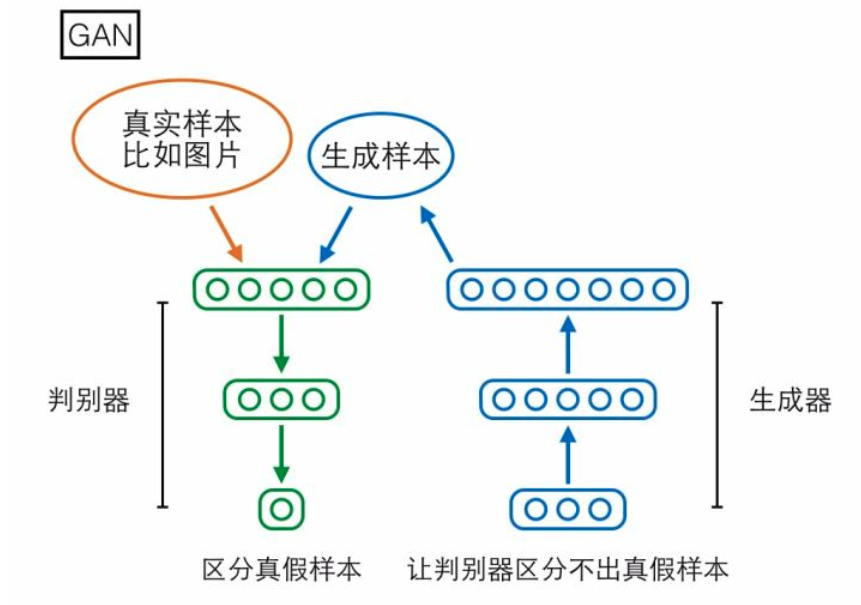
GAN的生成器输入一个100维的编码向量,但在生成样本的过程中未必会用上全部维度,可能有些维度提供了绝大部分重要信息,另外一些维度只是陪衬,提供一些无关痛痒的随机扰动。然而究竟哪些维度编码了重要信息,哪些维度仅仅提供随机扰动?在GAN的架构下我们既没法知道,也没法控制。
第二个模型InfoGAN却可以做到。先来看它的结构,相比GAN多了个重构器模块,用于重构生成器输入的随机编码向量,但是只重构由我们指定的一部分维度。
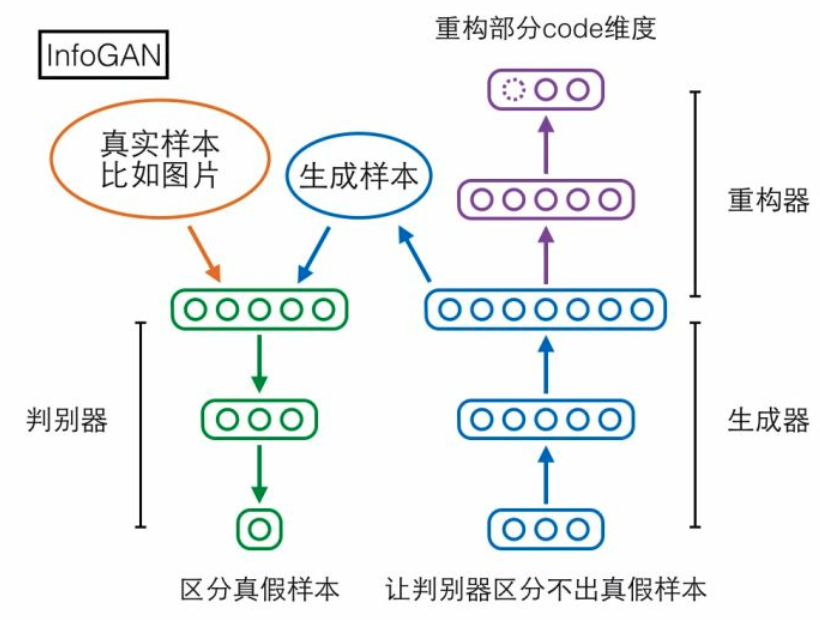
加上重构器模块之后,如果生成器拿这一部分维度当成无关痛痒的随机扰动来用,那重构器的任务就会比较艰难;但如果生成器拿这一部分维度当成样本的重要信息(或者套用PCA的术语,主成分)来用,那么输出样本就会和这部分编码维度高度相关,此时重构器能够比较轻松地从样本重构出原来的这部分编码。两相对比,生成器就会倾向于使用我们指定的这一部分维度来作为样本的重要信息(主成分)。训练结束后,甚至有机会观察到有些维度具有非常显著的语义信息,比如InfoGAN论文在MNIST手写数字上训练之后,可以观察到某个维度完全控制着0-9的数字类别,某个维度完全控制着数字图像从左到右的倾斜程度,这些显然就是MNIST数据集的重要信息(主成分):

对于已经读过InfoGAN论文的人,我需要补充解释一下,上述讲法跟论文的讲法不太一样。论文是从互信息的角度开始推导,经过一些变分推断的技巧最终得到模型的loss,但其实最终得到的loss基本上就是普通的重构误差。对于离散维度,论文最终推出的loss是log likelihood,一般对离散维度设置的重构误差也是如此;对于连续维度,论文最终推出的loss是对多维高斯分布取log,如果简化高斯分布中的协方差矩阵是单位矩阵,该loss就等价于普通的L2 loss,也是一般对连续维度设置的重构误差形式。
无论是GAN、InfoGAN还是其他GAN变种,基本上都想学习从零均值、一方差的标准高斯分布到复杂样本分布的映射,而GAN的思路是先固定前者(标准高斯分布)作为网络输入,再慢慢调整网络输出去匹配后者(复杂样本分布)。
第三个模型Adversarial Autoencoder(对抗自编码器)却采取了相反的思路!它是先固定后者(复杂样本分布)作为网络输入,再慢慢调整网络输出去匹配前者(标准高斯分布)。具体来说,对抗自编码器包含三个模块——编码器、解码器、判别器,前两者构成一个普通的自编码器,输入的复杂样本,还是要求在解码器的输出端重构;判别器输入编码向量,判定它是来自一个真实的标准高斯分布,还是来自编码器的输出。判别器试图区分编码向量的真假,编码器就试图让判别器区分不出真假,如果最终编码器赢了,就意味着它输出的编码很接近标准高斯分布,导致判别器混淆不清,我们的目的也就达到了。对抗自编码器严格来说应该不算GAN的变种,因为它的思路方向与GAN相反。
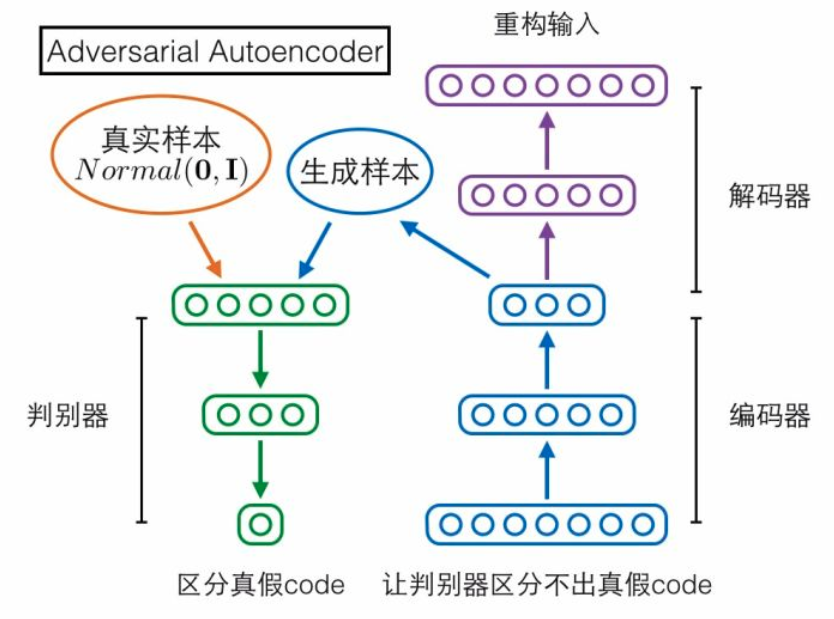
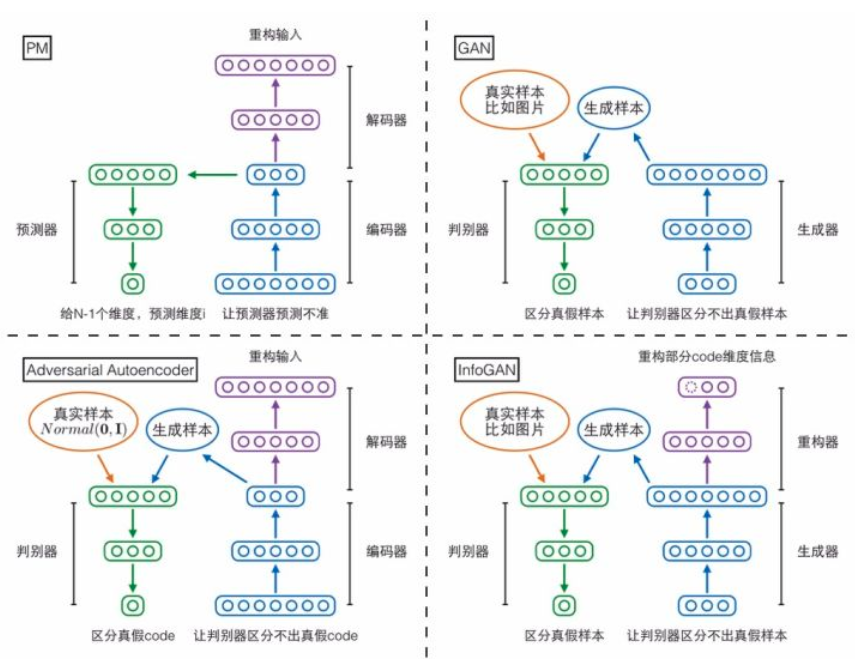
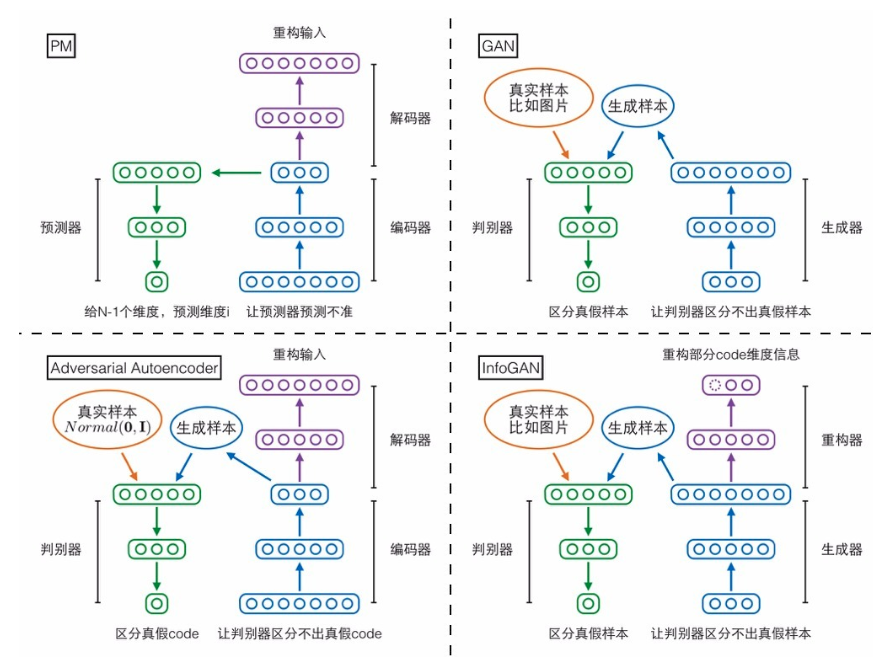
说到跟GAN方向相反,读者可能会记起上文提到Schmidhuber把GAN叫做“inverse PM”。PM跟GAN相反,对抗自编码器也和GAN相反,那它们两个会不会很像呢?答案是确实很像,如果把PM的架构图参照上面三个模型重新画一遍,就可以很清晰地看到PM跟对抗自编码器的主体架构完全对的上。
需要注意的是,上图其实把N个预测器合并画成了一个。
最后,一图总结第三部分:
四、纵横融汇
最后是对上述四个模型做综合比较。首先对比PM和GAN:
1.映射方向相反
- PM的编码器把复杂分布映射为解耦分布
- PM的解码器把解耦分布映射为复杂分布
- GAN的生成器把一个解耦的高斯分布映射为复杂分布
其中PM的编码器和GAN的生成器方向相反,所以Schmidhuber把GAN称为“inverse PM”。
2.都是对抗优化相反的目标
- PM的预测器要猜准某一维编码,编码器要让它猜不准
- GAN的判别器要区分真假样本,生成器要让它区分不准
3.预测/判别结构相似
如果把真假标签的节点跟图片样本节点拼接到一起,视为一个超长向量的话,GAN的判别器就可以强行视为PM预测器的特例:PM对每一个维度都要预测,但是GAN只预测真假标签这一特殊维度。

- PM的主体是自编码重构,对抗训练仅仅作为一个正则,起到辅助作用
- GAN的主体就是对抗训练,没有其他目标
5.可拓展性不同
- PM的思想最多只能做到把编码建模为解耦分布,没办法施加其他要求,施加其他要求那就不是PM的功劳了
- GAN虽然具体把编码建模为解耦高斯分布,但其实对编码的分布并没有任何限制,完全可以直接换成其他分布来建模,无论是均匀分布还是别的什么分布都没问题,甚至可以用另一个复杂分布比如图片来作为编码,让生成器输入一张图片输出另一张图片,可拓展性非常强大。
Goodfellow在GAN论文中还提了其他不同点,但是我个人觉得不合理,就忽略不讲了。经过上述比较,我们可以看到PM和GAN确实有非常多的相似之处,但是差异也很大,我个人觉得并不能把GAN简单看作PM的变种。
相比之下,PM和InfoGAN、对抗自编码器反倒更像:
1.模型主体
- PM主体是自编码器,要求重构复杂分布的样本
- 对抗自编码器主体是自编码器,要求重构复杂分布的样本
- InfoGAN主体可以视为自编码器,要求重构(部分)编码向量
2.对网络中间层的要求
- PM要求编码器和解码器中间的隐藏层解耦,它是通过可预测性最小化的思想来做到的
- 对抗自编码器要求编码器和解码器中间的隐藏层解耦,且满足高斯分布,它是通过对抗训练,拉近隐藏层编码分布与一个真正的解耦高斯分布来做到的
- InfoGAN要求生成器和重构器中间的隐藏层满足复杂样本分布,它是通过对抗训练,拉近生成分布与真实复杂分布来做到的
3.预测/判别结构相似
PM输入编码其他维度,预测某一维度;对抗自编码器,输入编码全部维度,预测真假标签;InfoGAN和前面GAN的情况相同,输入图片,预测真假标签。在这个角度上对抗自编码器与PM更相似。

inference.vc是一个关于生成模型的著名博客,其中有篇文章认为对抗自编码器中用GAN来拉近编码分布和高斯分布,是杀鸡用牛刀的做法。
文章认为,GAN模型强大的分布拉近能力适用于图片这样的复杂分布,但是对于像解耦高斯分布如此简单的情况,并不需要动用到GAN这种大杀器,其实完全可以利用解耦高斯分布的特殊形式,采取更加高效的方式(比如文章中提了一个叫做MMD的方法,此处略过不讲)。
看了PM之后就可以想到另一个思路——分别要求解耦和高斯。先把对抗自编码器的判别器换成PM模型的N组预测器,用可预测性最小化的思想,实现编码向量各个维度之间的解耦;接着对每个单独的编码维度,通过GAN使其满足高斯分布。虽然还是用GAN,但是我们把向量上的对抗训练转化为标量上的对抗训练,而后者可能比前者要容易和稳定得多。
五、总结
Schmidhuber在92年提出的PM模型通过可预测性最小化来学习一个解耦的编码表示,编码器和预测器优化相反的目标,确实是比GAN更早地使用了对抗训练的思想。
PM不仅跟GAN,还跟InfoGAN、对抗自编码器存在很多相似之处,但还是有很明显的差异。其中PM和对抗自编码器最像,主体都是自编码器,但它们并不能简单地视为GAN的变种。
我们现在都是盯着最新最前沿的研究工作,其实也许有很多像PM这样“古老”但有趣的想法被我们忽视了,有的是因为当年提出的时候思想太过超前,或者硬件计算能力撑不起来,导致无人问津,最典型的例子就是LSTM。这些工作不应该被埋没,如果能够重新挖掘出来的话,就可能给今天的研究带来很多新的启发。