【模板】并查集

　　并查集是解决两元素是否属于同一集合，将一个集合合并另一集合的数据结构。具体来说，我们使用数字代替集合，比如集合1，集合2.使用数组f[i]维护元素i属于的集合，比如f[2] = 4表示元素2属于集合4。具体我们有以下实现功能的代码

1 初始化表示集合的数组。

    cin>>n>>m;
    for(int i=1; i<=n; i++)
        f[i]=i;

 

 　　表示元素i属于集合i，也就是说开始每个元素都是散开的。

2 实现查找功能的find()函数

int find(int x)
{
    if(f[x]!=x) return f[x]=find(f[x]);
    return x;
};

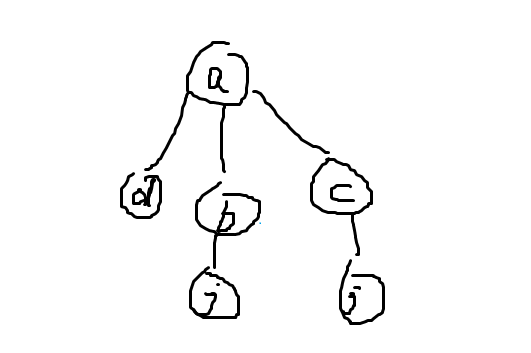
具体说明以下怎么实现的查找到的根结点（图有点丑）

 

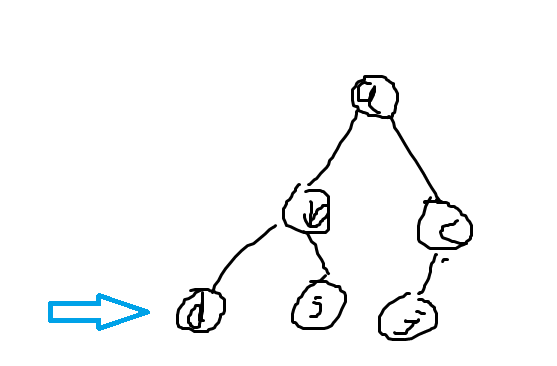
 以结点d为例，假设我们查找结点d属于那个集合也就是查找到这颗树的根结点。

从系统栈层面解释。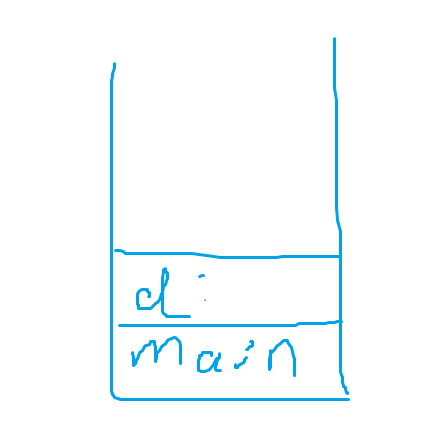

 

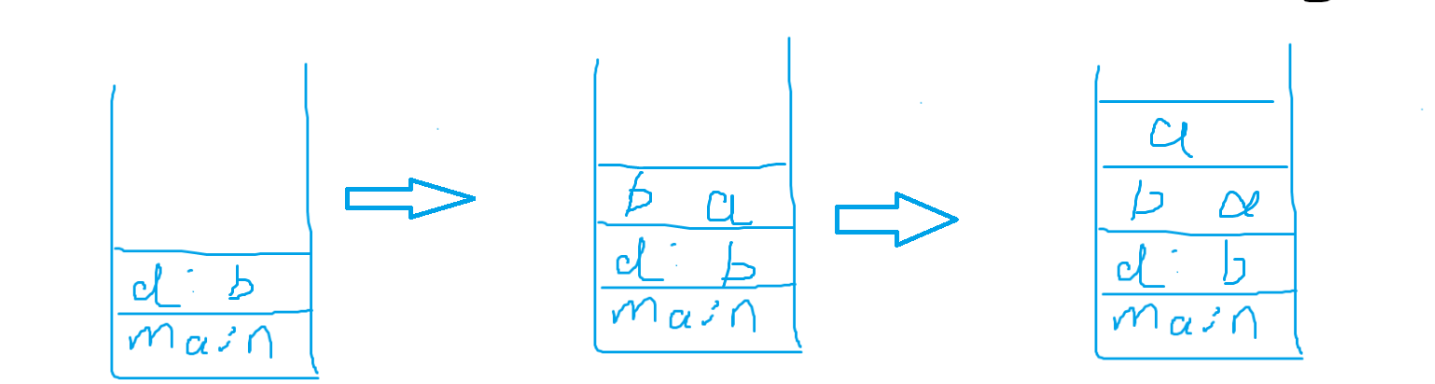
 可以看到到达结点a之后，返回栈开始返回。

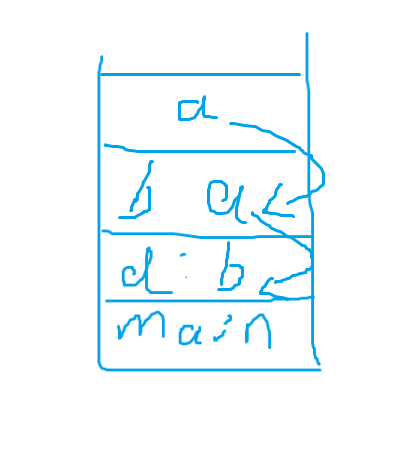
 结点a从上到下赋值给路径上的所有结点。那么这棵树就变成这样。

 这就是路径压缩。

3 合并函数join()

void join (int x,int y)
{
    int fx=find(x),fy=find(y);
    if(fx!=fy)     f[fx]=fy;
};

 

　　假设合并元素x，y所在集合首先find(x),find(y)找到元素x，元素y属于那个集合。

　然后将f[fx] 赋值为 fy，也就是x所在集合加入y所在集合。

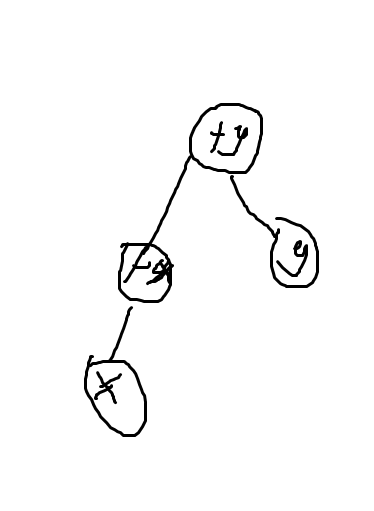
 实现了合并。

 4 维护特征的并查集（带权并查集）

　　例题：837. 连通块中点的数量 https://www.acwing.com/problem/content/839/

　　只需要多增加一个数组siz[]来储存集合i的大小即可。初始化siz[i] = 1;

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e5 + 10;
int n,m;

int f[maxn],size_f[maxn];

int find(int x){
    if(f[x] != x) return f[x] = find(f[x]);
    else return f[x];
}

void join(int x,int y){
    int x1 = find(x),y1 = find(y);
    if(x1 != y1) {
        size_f[y1] += size_f[x1]; // 主要维护集合fy的大小。
        f[x1] = y1;
    }
}
signed main ()
{
    cin>>n>>m;
    
    for(int i = 1; i<= n; i++){
        f[i] = i;
        size_f[i] = 1;
    }
    while(m--){
        string op;
        cin>>op;
        if(op == "C"){
            int a,b;
            cin>>a>>b;
            join(a,b);
        }else if(op == "Q1"){
            int a,b;
            cin>>a>>b;
            printf(find(a) == find(b) ? "Yes\n":"No\n");
        }else if(op == "Q2"){
            int a;
            cin>>a;
            printf("%d\n",size_f[find(a)]);
        }
    }
    return 0;
}