【SPFA】最短路的一种算法

　　SPFA算法是在bellman-ford算法基础上优化而来，所以我们先讨论bellman-ford算法

bellman-ford算法的核心是‘松弛’。那么什么是松弛呢？以下图为例：

　　假设数组d[i]表示源点s到达结点i的最短路径长度，那么松弛指的就是当d[a] + w < d[b]，也就是说，这时候通过a到达b比原来的路径更短，此时，我们松弛d[b] = d[a] + w;

　　bellman-ford算法核心思想简单，就是对m条边进行n-1次松弛操作，得到最短路径，如果还能松弛，说明存在负权环。如下所示

　　

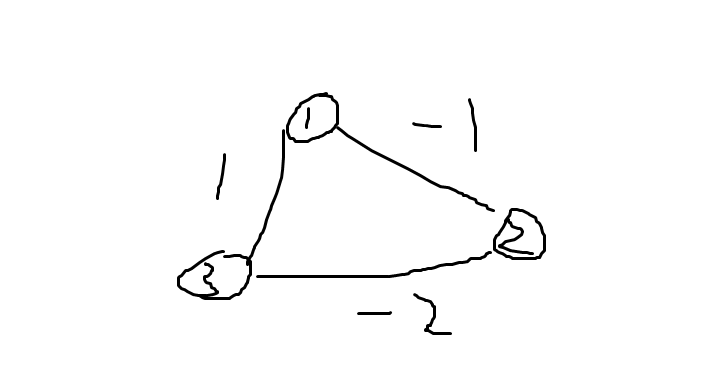
　　如果一直绕着负环，那么负环上的结点的最短距离都是-INF。

　　bellman-ford算法的伪代码如下

 　　

 　　我的代码：

void bellman(){
    fill(d,d + maxn,INF);
    d[1] = 0;
    
    for(int i = 1; i <= n-1; i++){
        memcpy(backup,d,sizeof d);
        for(int j = 1; j <= m; j++){
            int v = edg[j].v;
            int u = edg[j].u;
            int w = edg[j].w;
            d[v] = min(d[v],backup[u] + w);
        }
    }
}

　　backup数组是因为外层循环还有另一层含义，就是经过最多i条边，能完成的最短路径生成。

 

　　注意到，一个结点被更新是由于它的起始结点被更新，那么，我们使用bfs优化，将被更新的结点储存下来，这里要注意，需要使用inq[]数组储存结点是否在队列中。

　　以下是SPFA代码(非常像Dijkstr)：

bool SPFA(){
    memset(d,0x3f,sizeof d);
    queue<int> q;
    //1 q中元素都是被更新过的结点，为了防止重复更新结点，需要设置
    //cnt[i] 表示到达结点i最短路径经过的边数
    for(int i = 1; i <= n; i++){
        inq[i] = true;
        q.push(i);
    }
    //这个for循环是有些题目是判断是否有负环，而不是是否有从1开始的负环，那么我们就将所有结点入队。
    while(!q.empty()){
        int u = q.front();
        q.pop();
        inq[u] = false;
        
        int len = G[u].size();
        for(int i = 0; i < len; i++){
            int v = G[u][i].first;
            int w = G[u][i].second;
            if(d[u] + w < d[v]){
                d[v] = d[u] + w;
                if(!inq[v]){
                    q.push(v);
                    cnt[v] = cnt[u] + 1;
                    inq[v] = true;
                    if(cnt[v] >= n) return false;
                }
            }
        }
    }
    
    
    return true;
}

　　值得注意的是，cnt数组起到了和bellman-ford算法外循环类似的作用。一般来说，有负权边的问题都需要bellman-ford或者SPFA算法，但是正权边也可以先使用SPFA算法（虽然可能被卡，但是速度快）。