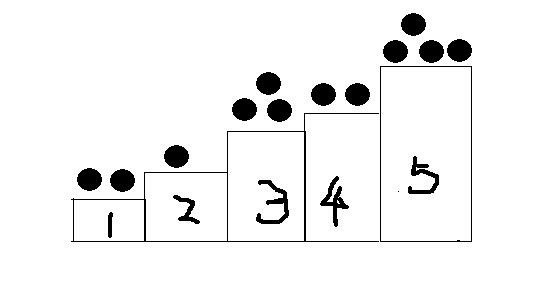
首先是对阶梯博弈的阐述...博弈在一列阶梯上进行...每个阶梯上放着自然数个点..两个人进行阶梯博弈...每一步则是将一个集体上的若干个点( >=1 )移到前面去..最后没有点可以移动的人输..
如这就是一个阶梯博弈的初始状态 2 1 3 2 4 ... 只能把后面的点往前面放...如何来分析这个问题呢...其实阶梯博弈经过转换可以变为Nim..把所有奇数阶梯看成N堆石子..做nim..把石子从奇数堆移动到偶数堆可以理解为拿走石子..就相当于几个奇数堆的石子在做Nim..( 如所给样例..2^3^4=5 不为零所以先手必败)为什么可以这样来转化?
假设我们是先手...所给的阶梯石子状态的奇数堆做Nim先手能必胜...我就按照能赢的步骤将奇数堆的石子移动到偶数堆...如果对手也是移动奇数堆..我们继续移动奇数堆..如果对手将偶数堆的石子移动到了奇数堆..那么我们紧接着将对手所移动的这么多石子从那个偶数堆移动到下面的奇数堆...两次操作后...相当于偶数堆的石子向下移动了几个..而奇数堆依然是原来的样子...即为必胜的状态...就算后手一直在移动偶数堆的石子到奇数堆..我们就一直跟着他将石子继续往下移..保持奇数堆不变...如此做下去..我可以跟着后手把偶数堆的石子移动到0..然后你就不能移动这些石子了...所以整个过程..将偶数堆移动到奇数堆不会影响奇数堆做Nim博弈的过程..整个过程可以抽象为奇数堆的Nim博弈...
其他的情况...先手必输的...类似推理...只要判断奇数堆做Nim博弈的情况即可...
为什么是只对奇数堆做Nim就可以...而不是偶数堆呢?...因为如果是对偶数堆做Nim...对手移动奇数堆的石子到偶数堆..我们跟着移动这些石子到下一个奇数堆...那么最后是对手把这些石子移动到了0..我们不能继续跟着移动...就只能去破坏原有的Nim而导致胜负关系的不确定...所以只要对奇数堆做Nim判断即可知道胜负情况...
附加题目:
POJ 1704
【题意】
从左到右有一排石子,给出石子所在的位置。规定每个石子只能向左移动,且不能跨过前面的石子。最左边的石子最多只能移动到1位置。每次选择一个石子按规则向左移动,问先手是否能赢。
【分析】
我们把棋子按位置升序排列后,从后往前把他们两两绑定成一对。如果总个数是奇数,就把最前面一个和边界(位置为0)绑定。
在同一对棋子中,如果对手移动前一个,你总能对后一个移动相同的步数,所以一对棋子的前一个和前一对棋子的后一个之间有多少个空位置对最终的结果是没有影响的。
于是我们只需要考虑同一对的两个棋子之间有多少空位。
这样一来就成了N堆取石子游戏了.
HDU 4315
【题意】
有N个人爬山,山顶坐标为0,其他人的坐标按升序给出。不同的坐标只能容纳一个人(山顶不限),Alice和Bob轮流选择一个人让他移动任意步,但不能越过前面那个人。现在有一个人是king(给出id),谁能将king移动到山顶就算赢。
【分析】
考虑King的情况和上述版本几乎一致,只要把King当作普通人一样处理即可。
除了两种特殊情况:
1. 当King是第一个人时,Alice直接胜
2. 当King是第二个人且一共有奇数个人时,第一堆的大小需要减1。
因为如果king在奇数石子上,那么king前面的那一对石子k1,k2.
当对方把k1移到top时,我可以把k2移到top前的一个位置.
那么对于k2石子,对方如果碰了它,那么我肯定会把king移到top的.
所以k2也相当于是一颗废子而已,不影响最终Nim的结果.