二叉树的深度优先遍历和广度优先遍历

1.二叉树的遍历方法

1）层次遍历（广度遍历）

　　自上而下，从左往右依次遍历　　

2）深度遍历

　　先序遍历：先访问根结点、再先序遍历左子树、再先序遍历右子树

　　中序遍历：先中序遍历左子树、再访问根结点、再中序遍历右子树

　　后序遍历：先后序遍历左子树、再后序遍历右子树、最后访问根结点

案例

　　

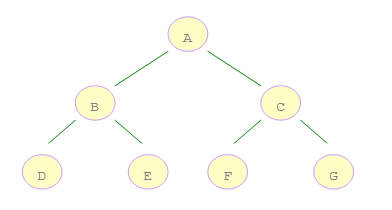
　　层次遍历：A 、B、C、D、E、F、G

　　先序遍历：A、B、D、E、C、F、G

　　中序遍历：D、B、E、A、F、C、G

　　后序遍历：D、E、B、A、F、G、C

2.二叉树结构

class TreeNode():
    def __init__(self,value=None,left=None,right=None):
        self.value = value
        self.left = left
        self.right = right

 3.实现

1）层次遍历（广度遍历）

def levelorder(root):
    if root is None:
        return None
    #模拟队列
    q = []
    #先将根结点入队列
    q.append(root)
    #列表为空时，循环终止
    while len(q) != 0:
        for i in range(len(q)):
            #将列表中第一个节点出队
            r = q.pop(0)
　　　　　　　　#每一次节点出队都将其左孩子和右孩子入队
            if r.left is not None:
                #左孩子入队
                q.append(r.left)
            if r.right is not None:
　　　　　　　　　　#右孩子入队
                q.append(r.right)
            print(r.value)

　2）深度遍历　（递归）

# 前序遍历
def preTraverse(root):
    if root is None:
        return
    print(root.value)
    preTraverse(root.left)
    preTraverse(root.right)
#中序遍历
def midTravrse(root):
    if root is None:
        return
    midTravrse(root.left)
    print(root.value)
    midTravrse(root.right)
#后续遍历
def afterTraverse(root):
    if root is None:
        return
    afterTraverse(root.left)
    afterTraverse(root.right)
    print(root.value)

 

非递归实现方法有时间补上