为了能到远方，脚下的每一步都不能少.|
收藏闪存小组博问

Aurora-JC

园龄：3年1个月粉丝：3关注：4

📂学习笔记
🔖可持久化可持久化线段树可持久化并查集可持久化平衡树可持久化 Trie
2023-09-10 15:11阅读: 27评论: 0推荐: 0

* 【学习笔记】(25) 可持久化数据结构

可持久化线段树（**树）

**树，一个数据结构，能访问到历史版本的数据，常用于可持久化和区间k大值，是线段树的一个升级版。

可持久化的意思是可以访问任意版本的数据，一眼想到的暴力做法就是开n个数组来记录，这显然是不可取的。

那么我们考虑优化。若只有单点修改，不难发现每两个版本的差别最多为1，那么我们是不是可以只更改只一个数呢？

显然是可以的。在线段树上，我们每访问到一个节点，如果该节点没有被修改，直接用指针指想该节点即可（和动态开点线段树类似）

要注意的是，我们不能像以前一样用u∗2 表示左儿子，u∗2+1表示右儿子了（如果你用动态开点就当我没说），而是要用 ls[u]/ls[y] 代表左右儿子。

那我们怎么访问每一个版本呢？我们只需要对每一个版本存储一个根节点，从根节点访问就行了

这样我们就可以很好的来处理可持久化的问题了。

这里放张图

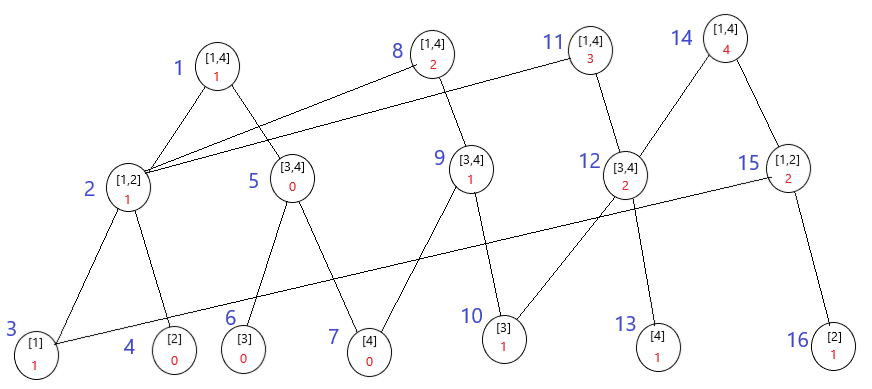
标记永久化

对于区间修改的题目，虽然可以通过下推标记维护信息，但是每次下推标记时，如果没有左右儿子，那么就要新建节点，空间开销过大。

不妨不下推标记，仅在查询时计算标记的贡献。常见于区间加 + 查询区间和/最值中，因为加法可以累积，即查询时额外储存从根节点到当前区间表示节点的标记和，再加上该区间所存储的值就是当前值。

如果是区间赋值，那么可以在标记中额外维护时间戳，查询时找到时间戳最大的那一次修改的权值即为当前值。

SP11470 TTM - To the moon

这题先上来写一个**树，像线段树那样打区间加标记，但是马上就发现不能 pushdown。

因为：**树是有共用子结点的，直接把标记传递下去会影响答案的正确性，如果新建一大堆结点那复杂度就大到飞起还不如暴力跑得快。所以需要使用标记永久化。

标记永久化就是每个结点维护一个add标记，表示这个区间每个数加上了 x。每个结点维护的区间和s，通过子结点的s之和加上左右儿子的add标记乘以区间长度来维护。这就是说，一个结点对应的区间被整体加上一个值，从根到这个结点的路径上所有结点的s都会被更新，而对它子树内的结点的影响等到询问的时候再考虑。

细节见代码，询问的时候用如下方式写会比较简单，不需要判区间交的长度。

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int n, m, curt, cnt;
int rt[N], ls[N << 6], rs[N << 6], a[N];
ll val[N << 6], ad[N << 6];
 
void build(int &u, int l, int r){
	u = ++cnt;
	if(l == r) return val[u] = a[l], void();
	int mid = (l + r) >> 1;
	build(ls[u], l, mid), build(rs[u], mid + 1, r);
	val[u] = val[ls[u]] + val[rs[u]];
}
 
void modify(int &u, int v, int l, int r, int L, int R, int x){
	u = ++cnt, ls[u] = ls[v], rs[u] = rs[v];
	val[u] = val[v], ad[u] = ad[v];
	if(L <= l && r <= R) return ad[u] += x, void();
	int mid = (l + r) >> 1;
	if(L <= mid) modify(ls[u], ls[v], l, mid, L, R, x);
	if(R > mid) modify(rs[u], rs[v], mid + 1, r, L, R, x);
	val[u] = val[ls[u]] + val[rs[u]] + (mid - l + 1) * ad[ls[u]] + (r - mid) * ad[rs[u]];
}
 
ll query(int u, int l, int r, int L, int R){
	if(L <= l && r <= R) return val[u] + ad[u] * (r - l + 1);
	int mid = (l + r) >> 1; ll ans = ad[u] * (min(R, r) - max(l, L) + 1);
	if(L <= mid) ans += query(ls[u], l, mid, L, R);
	if(R > mid) ans += query(rs[u], mid + 1, r, L, R);
	return ans; 
}
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(), m = read();
	for(int i = 1; i <= n; ++i) a[i] = read();
	char opt[67]; 
	build(rt[0], 1, n);
	for(int i = 1, l, r, t; i <= m; ++i){
		scanf("%s", opt + 1);
		if(opt[1] == 'C'){
			l = read(), r = read(), t = read();
			modify(rt[curt + 1], rt[curt], 1, n, l, r, t);
			curt++;
		}else if(opt[1] == 'Q'){
			l = read(), r = read();
			printf("%lld\n", query(rt[curt], 1, n, l, r));
		}else if(opt[1] == 'H'){
			l = read(), r = read(), t = read();
			printf("%lld\n", query(rt[t], 1, n, l, r));
		}else curt = read();
	}
	return 0;
}

应用：静态区间第 k 小

首先将权值离散化（当然不离散化直接动态开点也可以，不过常数会稍大一些）。

运用前缀和的思想，按照下标顺序依次将每个值加入维护出现次数的线段树，并运用**树维护每次修改后线段树的形态。这样，将第 r 棵线段树的所有值减去第 l−1 棵线段树上对应的值，即为 al∼r 中所有数所建出的线段树，每个节点的值为 al∼r 中有多少个数的值落在该节点所表示的区间中。

显然我们不能完全建出 al∼r 表示的线段树，不过其实并不需要这么做。运用线段树二分的思想，如果当前区间的左儿子的值（记为 v，显然 v=vallsy−vallsx，其中 x,y 分别是第 l−1 和第 r 棵线段树当前节点的编号）不小于 k，也即有不小于 k 个 al∼r 中的数的值落在该节点左儿子所表示的区间中。此时向左儿子递归查询即可。否则将 k 减去 v ，再向右儿子递归查询。

时间复杂度 nlogn∼nlogc ，其中 c 是值域。

例题

1. P3919 【模板】可持久化线段树 1（可持久化数组） 

#include<bits/stdc++.h>
#define N 1000005
using namespace std;
void read(int &x){
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<1)+(x<<3)+(s^48);s=getchar();}
    x*=f;
}
struct Node{
	int l,r,val;
}node[N<<5];
int n,m,cnt;
int a[N],root[N];
int Build(int L,int R){
	int u=++cnt,m=(L+R)>>1;
	if(L>=R){
		node[u].val=a[L];
		return u;
	}
	node[u].l=Build(L,m);
	node[u].r=Build(m+1,R);
	return u;
}
int Query(int u,int L,int R,int pos){
	if(L==R) return node[u].val;
	int m=(L+R)>>1;
	if(m>=pos) return Query(node[u].l,L,m,pos); 
	else return Query(node[u].r,m+1,R,pos);
}
int UpDate(int pre,int L,int R,int pos,int val){
	int u=++cnt;
	node[u].l=node[pre].l,node[u].r=node[pre].r,node[u].val=node[pre].val;
	int m=(L+R)>>1;
	if(L==R){
		node[u].val=val;
		return u;
	} 
	if(pos<=m) node[u].l=UpDate(node[pre].l,L,m,pos,val);
	else node[u].r=UpDate(node[pre].r,m+1,R,pos,val);
	return u;
}
int main(){
	read(n),read(m);
	for(int i=1;i<=n;i++) read(a[i]);
	root[0]=Build(1,n);
	for(int i=1;i<=m;i++){
		int rt,opt,pos,val;
		read(rt),read(opt),read(pos);
		if(opt==1){
			read(val);
			root[i]=UpDate(root[rt],1,n,pos,val);
		}else{
			printf("%d\n",Query(root[rt],1,n,pos));	
			root[i]=root[rt];
		}
		//printf("%d\n\n",root[i]);
	}
	return 0;
}

2. P3834 【模板】可持久化线段树 2 

#include<bits/stdc++.h>
#define N 200005
using namespace std;
void read(int &x){
    int f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<1)+(x<<3)+(s^48);s=getchar();}
    x*=f;
}
int a[N],root[N],b[N];
int n,m,cnt;
struct Node{
	int l,r,sum;
}node[N<<5];
int Build(int L,int R){
	int u=++cnt,mid=(L+R)>>1;
	node[u].sum=0;
	if(L<R){
		node[u].l=Build(L,mid);
		node[u].r=Build(mid+1,R); 
	}
	return u;
}
int UpDate(int pre,int L,int R,int x){
	int u=++cnt;
	node[u].sum=node[pre].sum+1;
	node[u].l=node[pre].l,node[u].r=node[pre].r;
	int mid=(L+R)>>1;
	if(L<R){
		if(x<=mid) node[u].l=UpDate(node[pre].l,L,mid,x);
		else node[u].r=UpDate(node[pre].r,mid+1,R,x);
	}
	return u;
} 
int Query(int u,int v,int L,int R,int k){
	if(L>=R) return L;
	int x=node[node[v].l].sum-node[node[u].l].sum,mid=(L+R)>>1;
	if(x>=k) return Query(node[u].l,node[v].l,L,mid,k);
	else return Query(node[u].r,node[v].r,mid+1,R,k-x);
}
int main(){
	read(n),read(m);
	for(int i=1;i<=n;i++) read(a[i]),b[i]=a[i];
	sort(b+1,b+1+n);
	int tot=unique(b+1,b+1+n)-b-1;  
	root[0]=Build(1,tot);
	for(int i=1;i<=n;i++){
		int x=lower_bound(b+1,b+tot+1,a[i])-b;
		root[i]=UpDate(root[i-1],1,tot,x);
	}
	while(m--){
		int l,r,k;
		read(l),read(r),read(k);
		int id=Query(root[l-1],root[r],1,tot,k);
		printf("%d\n",b[id]);
	}
	return 0;
}

3. P2839 [国家集训队] middle

显然答案满足可二分性，将其转化为 “中位数是否 ≥x”：所有 <x 的数视作 −1，≥x 的数视作 1，则题目转化为求端点分别在 [a,b]，[c,d] 的区间之和最大值是否不小于 0，可以进一步转化为 [a,b) 的最大可空后缀和 + [b,c] 的和 + (c,d] 的最大可空前缀和，这个用线段树可以轻松维护。然后用**树建立每一个值的值域线段树即可。

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int n, cnt, q, las, ans;
int b[N], rt[N], ls[N << 5], rs[N << 5], c[67];
struct node{
	int id, tr;
	bool operator < (const node &A) const{return tr < A.tr;}
}a[N];
 
struct Tree{
	int sum, pre, suf;
	friend Tree operator + (Tree a, Tree b){
		Tree c; c.sum = a.sum + b.sum;
		c.pre = max(a.pre, a.sum + b.pre);
		c.suf = max(b.suf, b.sum + a.suf);
		return c;
	}
}tr[N << 5];
 
void build(int &u, int l, int r){
	u = ++cnt; tr[u] = (Tree){r - l + 1, r - l + 1, r - l + 1};
	if(l == r) return ;
	int mid = (l + r) >> 1;
	build(ls[u], l, mid), build(rs[u], mid + 1, r);
	tr[u] = tr[ls[u]] + tr[rs[u]]; 
}
 
void modify(int &u, int v, int l, int r, int p){
	u = ++cnt, tr[u] = tr[v], rs[u] = rs[v], ls[u] = ls[v];
	if(l == r) return tr[u] = {-1, 0, 0}, void();
	int mid = (l + r) >> 1;
	if(p <= mid) modify(ls[u], ls[v], l, mid, p);
	else modify(rs[u], rs[v], mid + 1, r, p);
	tr[u] = tr[ls[u]] + tr[rs[u]];
}
 
Tree query(int u, int l, int r, int L, int R){
	if(L <= l && r <= R) return tr[u];
	int mid = (l + r) >> 1; Tree res = {0, 0, 0};
	if(L <= mid) res = res + query(ls[u], l, mid, L, R);
	if(R > mid) res = res + query(rs[u], mid + 1, r, L, R);
	return res;
}
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(); build(rt[0], 1, n);
	for(int i = 1; i <= n; ++i) b[i] = a[i].tr = read(), a[i].id = i;
	sort(b + 1, b + 1 + n), sort(a + 1, a + 1 + n);
	for(int i = 1; i <= n; ++i) modify(rt[i], rt[i - 1], 1, n, a[i].id);
	q = read();
	while(q--){
		for(int i = 0; i < 4; ++i) c[i] = (read() + las) % n + 1;
		int l = 0, r = n - 1; sort(c, c + 4);
		while(l <= r){
			int mid = (l + r) >> 1;
			Tree lp = query(rt[mid], 1, n, c[0], c[1] - 1);
			Tree mp = query(rt[mid], 1, n, c[1], c[2]);
			Tree rp = query(rt[mid], 1, n, c[2] + 1, c[3]);
			if(lp.suf + mp.sum + rp.pre >= 0) l = mid + 1, ans = mid;
			else r = mid - 1;
		}
		printf("%d\n", las = b[ans + 1]);
	}
	return 0;
}

4. P3168 [CQOI2015] 任务查询系统

将一段区间拆成单点加减，然后就是裸的**树了。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int m, n, las = 1, cnt, mm;
int b[N], rt[N], ls[N << 5], rs[N << 5];
int sum[N << 5], val[N << 5];
 
struct xd{
	int s, p, val;
	bool operator < (const xd &A) const{return s < A.s;}
}c[N];
 
void modify(int &u, int v, int l, int r, int p, int x){
	u = ++cnt, val[u] = val[v] + x, sum[u] = sum[v] + b[p] * x;
	ls[u] = ls[v], rs[u] = rs[v];
	if(l == r) return ;
	int mid = (l + r) >> 1;
	if(p <= mid) modify(ls[u], ls[v], l, mid, p, x);
	else modify(rs[u], rs[v], mid + 1, r, p, x);
}
 
int query(int u, int l, int r, int k){
	if(l == r) return min(k, val[u]) * b[l];
	int mid = (l + r) >> 1;
	if(val[ls[u]] >= k) return query(ls[u], l, mid, k);
	else return sum[ls[u]] + query(rs[u], mid + 1, r, k - val[ls[u]]);
}
 
bool _v;
 
signed main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
//	freopen("1.in", "r", stdin);
//	freopen("1.out", "w", stdout);
	
	m = read(), n = read();
	for(int i = 1; i <= m; ++i){
		int s = read(), e = read(), p = read(); b[i] = p;
		c[i * 2 - 1] = {s, p, 1}, c[i * 2] = {e + 1, p, -1};
	}
	sort(b + 1, b + 1 + m), sort(c + 1, c + 1 + m * 2);
	mm = unique(b + 1, b + 1 + m) - b - 1; 
	for(int i = 1, p = 1; i <= n; ++i){
		bool flag = 0;
		while(p <= 2 * m && c[p].s <= i){
			int x = lower_bound(b + 1, b + 1 + mm, c[p].p) - b;
			modify(rt[i], flag ? rt[i] : rt[i - 1], 1, mm, x, c[p++].val), flag = 1;
		} 
		if(!flag) rt[i] = rt[i - 1];
	}
	for(int i = 1; i <= n; ++i){
		int x = read(), aa = read(), bb = read(), cc = read();
		int k = 1 + (aa * las + bb) % cc;
		printf("%lld\n", las = query(rt[x], 1, mm, k));
	}
	return 0;
}

5. P3293 [SCOI2016] 美味

类似 01Trie 从高位往低位贪心：设已经选择的所有位的数字为 d，如果 b 的这一位（i）是 0，那么看 al∼r 中是否有 [d+2i−x,d+2i+1−x)，反之亦然，**树即可。

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int m, n, cnt;
int rt[N], ls[N << 5], rs[N << 5], val[N << 5];
 
void modify(int &u, int v, int l, int r, int p){
	u = ++cnt, val[u] = val[v] + 1, ls[u] = ls[v], rs[u] = rs[v];
	if(l == r) return ;
	int mid = (l + r) >> 1;
	if(p <= mid) modify(ls[u], ls[v], l, mid, p);
	else modify(rs[u], rs[v], mid + 1, r, p);
}
 
int query(int u, int v, int l, int r, int L, int R){
	if(L > R) return 0;
	if(L <= l && r <= R) return val[u] - val[v];
	int mid = (l + r) >> 1, ans = 0;
	if(L <= mid) ans += query(ls[u], ls[v], l, mid, L, R);
	if(R > mid) ans += query(rs[u], rs[v], mid + 1, r, L, R);
	return ans;
}
 
bool _v;
 
signed main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(), m = read();
	for(int i = 1, a; i <= n; ++i) a = read(), modify(rt[i], rt[i - 1], 0, 1e5 - 1, a);
	while(m--){
		int b = read(), x = read(), l = read(), r = read(), d = 0;
		for(int i = 17; ~i; --i){
			int bit = (b >> i) & 1, c = (bit ^ 1) << i;
			int L = max(0, d + c - x), R = min((int)1e5 - 1, d + c + (1 << i) - x - 1);
			if(query(rt[r], rt[l - 1], 0, 1e5 - 1, L, R)) d += (bit ^ 1) << i;
			else d += (bit << i);
		}
		printf("%d\n", b ^ d);
	}
	return 0;
}

可持久化平衡树

可持久化(撤销)并查集

简介

基于可持久化数组。

因为每次 merge 两个集合时，只需要修改其中一个代表元指向的父节点，于是可以用可持久化数组维护回溯各个版本的并查集。

注意既要维护 fa 又要维护 size/dep ，因为不能用路径压缩（空间会炸），只能按秩合并。

如果只需要撤销，那么用栈维护修改再回溯即可。

应用

可持久化并查集可以用来维护边权有上界或下界时，所有合法的边所形成的连通块。具体地，将边按边权从小到大的顺序加入并查集，每加入一条边就记录一个版本的 fa 数组。这样每次查询代表元的时间复杂度是 log2n 的（查 fa log 加上深度的 log）。

如果给出 (u,v,w) 询问能否不经过权值不大于 w 的边从 u 走到 v，那么在加入最大的边权不大于 w 的边之后的那一个版本的并查集中查询 u,v 代表元是否相同即可。

例题

Ⅰ. P3402 可持久化并查集 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2.5e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int n, m, cnt;
int rt[N], ls[N << 5], rs[N << 5], fa[N << 5], sz[N << 5];
 
void build(int &u, int l, int r){
	u = ++cnt;
	if(l == r) return fa[u] = l, sz[u] = 1, void();
	int mid = (l + r) >> 1;
	build(ls[u], l, mid), build(rs[u], mid + 1, r);
}
 
void modify(int &u, int v, int l, int r, int p, int x, int tp){
	u = ++cnt, ls[u] = ls[v], rs[u] = rs[v], fa[u] = fa[v], sz[u] = sz[v];
	if(l == r) return tp == 1 ? fa[u] = x : sz[u] = x, void();
	int mid = (l + r) >> 1;
	if(p <= mid) modify(ls[u], ls[v], l, mid, p, x, tp);
	else modify(rs[u], rs[v], mid + 1, r, p, x, tp); 
} 
 
int query(int u, int l, int r, int p, int tp){
	if(l == r) return tp == 1 ? fa[u] : sz[u];
	int mid = (l + r) >> 1;
	if(p <= mid) return query(ls[u], l, mid, p, tp);
	else return query(rs[u], mid + 1, r, p, tp);
}
 
int find(int x, int id){
	int f = query(rt[id], 1, n, x, 1);
	return f == x ? x : find(f, id);
} 
 
void merge(int x, int y, int id){
	x = find(x, id), y = find(y, id);
	if(x == y) return rt[id + 1] = rt[id], void();
	int sx = query(rt[id], 1, n, x, 2), sy = query(rt[id], 1, n, y, 2);
	if(sx < sy) swap(sx, sy), swap(x, y);
	modify(rt[id + 1], rt[id], 1, n, y, x, 1);
	modify(rt[id + 1], rt[id + 1], 1, n, x, sx + sy, 2);
}
 
bool _v;
 
signed main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
//	freopen("6.in", "r", stdin);
	n = read(), m = read(); build(rt[0], 1, n);
	for(int i = 1; i <= m; ++i){
		int opt = read(), a, b, k;
		if(opt == 1){
			a = read(), b = read(); 
			merge(a, b, i - 1);
		}else if(opt == 2){
			k = read();
			rt[i] = rt[k];
		}else{
			a = read(), b = read();
			rt[i] = rt[i - 1];
			printf("%d\n", find(a, i) == find(b, i));
		}
	}
	return 0;
}

Ⅱ. P3247 [HNOI2016] 最小公倍数

Ⅲ. P5443 [APIO2019] 桥梁

如果没有修改，直接按照边权从大到小排序并查集维护即可。

带修就比较麻烦了，考虑分块：每个块内重构并查集，将询问和边从大到小排序，加边的时候如果这条边被修改那么跳过，每次询问的时候枚举所有被修改的边 ei(u,v,d)
，如果修改时间在查询时间之前且是最后一次修改 ei 且满足修改后的 d≥w 或者修改时间在查询时间之后且修改前的 d≥w 就往并查集里面加边 (u,v) ，询问完后回溯。

设块大小为 S ，则时间复杂度为 O(qSS2logn+qSmlogm)，实际测试下 S 取 mlog m 时跑得比较快。

#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pii pair<int, int>
using namespace std;
const int N = 1e5 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int n, m, q, B, cnt, ans[N];
 
struct edge{
	int u, v, w, id;
	bool operator < (const edge &A) const{return w > A.w;}
}e[N], g[N];
 
struct query{
	int t, x, y, id;
	bool operator < (const query &A) const{return y > A.y;}
}c[N];
bool cmp(query x, query y){return x.id < y.id;}
 
int fa[N], sz[N], tag[N];
int d, a[N], b[N], cha[N];
 
int find(int x){return fa[x] == x ? x : find(fa[x]);}
 
int merge(int x, int y){
	x = find(x), y = find(y);
	if(x == y) return 0;
	if(sz[x] < sz[y]) swap(x, y);
	sz[x] += sz[y], fa[y] = x, a[++d] = x, b[d] = y;
	return 1;
}
 
void cancle(){sz[a[d]] -= sz[b[d]], fa[b[d]] = b[d], --d;}
 
void solve(){
	for(int i = 1; i <= m; ++i) g[i] = e[i];
	sort(g + 1, g + 1 + m), memset(tag, 0, sizeof(tag)), memset(ans, -1, sizeof(ans));
	for(int i = 1; i <= cnt; ++i) if(c[i].t == 1) tag[c[i].x] = 1;
	for(int i = 1; i <= n; ++i) fa[i] = i, sz[i] = 1;
	sort(c + 1, c + 1 + cnt), d = 0;
	for(int i = 1, p = 1; i <= cnt; ++i){
		if(c[i].t == 1) continue;
		while(p <= m && g[p].w >= c[i].y){
			if(tag[g[p].id]){++p; continue;}
			merge(g[p].u, g[p].v); ++p;
		}
		int can = 0;
		for(int j = 1; j <= cnt; ++j)
			if(c[j].t == 1 && c[j].id < c[i].id) 
				cha[c[j].x] = max(cha[c[j].x], c[j].id);
		for(int j = 1; j <= cnt; ++j)
			if(c[j].t == 1){
				int id = c[j].x;
				if(!cha[id] && e[id].w >= c[i].y || (cha[id] == c[j].id && c[j].y >= c[i].y))
					can += merge(e[id].u, e[id].v);
			}
		ans[c[i].id] = sz[find(c[i].x)];
		for(int j = 1; j <= cnt; ++j) cha[c[j].x] = 0;
		while(can--) cancle();
	}
	sort(c + 1, c + 1 + cnt, cmp);
	for(int i = 1; i <= cnt; ++i){
		if(c[i].t == 1) e[c[i].x].w = c[i].y;
		else printf("%d\n", ans[i]);
	}
}
 
bool _v;
 
signed main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(), m = read(); B = m ? sqrt(m * log2(m)) : 2;
	for(int i = 1; i <= m; ++i) e[i].u = read(), e[i].v = read(), e[i].w = read(), e[i].id = i;
	q = read();
	for(int i = 1; i <= q; ++i){
		c[++cnt].t = read(), c[cnt].x = read(), c[cnt].y = read(), c[cnt].id = cnt;
		if(cnt == B) solve(), cnt = 0;
	} 
	if(cnt) solve();
	return 0;
}

可持久化 Trie

万物皆可可持久化。

类似可持久化线段树，插入一个数/字符串时新建节点。

其实可持久化 Trie 的结构和**树几乎一模一样，只不过 Trie 中每个节点所维护的区间长度是 2 的幂。这样一来可持久化 Trie 能做的事情基本上完全*含于**树能做的事情。

例题

Ⅰ. P5283 [十二省联考 2019] 异或粽子

我们要求出每个以 i 为结尾的区间的异或最大值，放入堆中，取出之后再将第 2 大值放入堆中，...依此类推。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5 + 67, B = 31;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
struct node{
	int val, id, kth;
	bool friend operator < (node a, node b){
		return a.val == b.val ? a.id < b.id : a.val < b.val;
	}
};
priority_queue<node> q;
 
int n, k, cnt;
int ans;
int a[N], pre[N], son[N << 6][2], rt[N], sz[N << 6];
 
void ins(int &u, int v, int vv, int b){
	u = ++cnt, sz[u] = sz[v] + 1;
	if(b < 0) return ;
	int c = (vv >> b) & 1;
	ins(son[u][c], son[v][c], vv, b - 1), son[u][c ^ 1] = son[v][c ^ 1];
}
 
int query(int u, int vv, int k, int b){
	if(b < 0) return 0;
	int c = (vv >> b) & 1, s = sz[son[u][c ^ 1]];
	if(k <= s) return (1ll << b) + query(son[u][c ^ 1], vv, k, b - 1);
	else return query(son[u][c], vv, k - s, b - 1);
} 
 
bool _v;
 
signed main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(), k = read(); ins(rt[0], rt[0], 0, B);
	for(int i = 1; i <= n; ++i) a[i] = read(), pre[i] = pre[i - 1] ^ a[i], ins(rt[i], rt[i - 1], pre[i], B);
	for(int i = 1; i <= n; ++i) q.push({query(rt[i - 1], pre[i], 1, B), i, 1});
	while(k--){
		node it = q.top(); q.pop(), ans += it.val;
		if(++it.kth <= it.id) q.push({query(rt[it.id - 1], pre[it.id], it.kth, B), it.id, it.kth});
	}
	printf("%lld\n", ans);
	return 0;
}

Ⅱ.CF241B Friends

Ⅲ. P4735 最大异或和

模板题。
a[p] xor a[p+1] xor ... xor a[n] xor x = s[p−1] xor s[n] xor

所以我们只要求 s[p] xor s[n] xor x 的最大值。

#include<bits/stdc++.h>
using namespace std;
const int N = 6e5 + 67, B = 24;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
 
bool _u;
 
int n, m, a, cnt;
int rt[N], ls[N << 5], rs[N << 5], val[N << 5];
 
void ins(int &u, int v, int a, int b){
	val[u = ++cnt] = val[v] + 1, ls[u] = ls[v], rs[u] = rs[v];
	if(b == 0) return ;
	if((a >> b - 1) & 1) ins(rs[u], rs[v], a, b - 1);
	else ins(ls[u], ls[v], a, b - 1);
}
 
int query(int v, int u, int vv, int b){
	if(b == 0) return 0;
	int bit = (vv >> b - 1) & 1;
	if(bit){
		if(val[ls[u]] - val[ls[v]]) return query(ls[v], ls[u], vv, b - 1) + (1 << b - 1);
		else return query(rs[v], rs[u], vv, b - 1);
	}else{
		if(val[rs[u]] - val[rs[v]]) return query(rs[v], rs[u], vv, b - 1) + (1 << b - 1);
		else return query(ls[v], ls[u], vv, b - 1);
	}
}
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read() + 1, m = read(); ins(rt[1], rt[0], 0, B);
	for(int i = 2; i <= n; ++i) ins(rt[i], rt[i - 1], a ^= read(), B);
	for(int i = 1, l, r; i <= m; ++i){
		char s; cin >> s;
		if(s == 'A') ++n, ins(rt[n], rt[n - 1], a ^= read(), B);
		else l = read(), r = read(), printf("%d\n", query(rt[l - 1], rt[r], a ^ read(), B));
	}
	return 0;
}

参考 :https://www.cnblogs.com/alex-wei/p/DS.html

本文作者：南风未起

本文链接：https://www.cnblogs.com/jiangchen4122/p/17678153.html

版权声明：本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。

posted @   Aurora-JC  阅读(27)  评论(0)  编辑  收藏  举报
点击右上角即可分享
微信分享提示
评论
收藏
关注
推荐
深色
回顶
收起