【学习笔记】(22) 点分治
点分治就是把分治搬到了树上，其核心思想仍然是分治：将问题经过处理后，转化为同类型的，规模更小的问题求解。
静态点分治
Ⅰ.P3806 【模板】点分治1
题意：给定一棵带权无根树，问是否有点对的距离为 \(k\)
假如我们要遍历树上所有的点对，最朴素的想法是枚举端点，对每个点来一趟 \(dfs\) ,复杂度 \(\mathcal{O}(n^2)\) 为了效率更高地解决问题，我们引入分治思想。对于每个点，我们分别考虑包含这个点的路径和不包含这个点的路径。对于前者，我们做一趟 \(dfs\)；对于后者，我们删除该点后，对所有子树递归地处理即可。
但是如果直接做，复杂度是不稳定的，例如当树是一条链时，有可能会退化成 \(\mathcal{O}(n^2)\)
。然而，如果每次都选择子树的重心，那么复杂度就可以保证为 \(\mathcal{O}(n \log n)\) 。因为重心的子树大小不超过 \(\frac{n}{2}\)
所以每次递归问题规模可以下降一半或以上。这种做法就叫做点分治。
找重心的话，可以用一次 \(dfs\)：
//sz[x]表示以x为根的子树大小，maxp[x]表示x的最大子树
void dfs(int x,int fa,int total){ //找重心
sz[x]=1,maxp[x]=0;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa||vis[y]) continue;
dfs(y,x,total);
sz[x]+=sz[y];
maxp[x]=max(maxp[x],sz[y]);
}
maxp[x]=max(maxp[x],total-sz[x]);//还有一棵以其父亲节点为根的子树
if(!ctr||maxp[x]<maxp[ctr]) ctr=x;//找到最优的根
}
找到重心后，我们需要不断分治，在分治过程中也需要不断找重心来优化，因为在找到重心后，其实子树size会发生变化，所以最好再以重心为根再dfs一遍 ，其实不再 \(dfs\) 的复杂度也是对的，可以看这里的证明：
void solve(int x){ //分治
vis[x]=1,calc(x);
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(vis[y]) continue;
ctr=0,dfs(y,-1,sz[y]),dfs(ctr,-1,sz[y]);
solve(ctr);
}
}
由于我们保证了所有的路径都是第一种（经过根节点的路径），所以我们对于每一个根，可以先预处理出每一个子节点到根的距离，这样我们就可以得到对于每一个点可能出现的距离
记当前的重心为 \(ctr\) 。
- \(a\) 数组记录 \(ctr\) 能到的点
- \(d\) 数组记录 \(a_i\) 到 \(ctr\) 的距离
- \(b\) 数组记录 \(a_i\) 属于 \(ctr\) 的哪棵子树（当 $b_{a_i} = b_{a_j} $ 时，说明 \(a_i\) 与 \(a_j\) 属于 \(root\) 的同一棵子树 ）
void gdis(int x,int fa,int dis,int from){
a[++tot]=x,d[x]=dis,b[x]=from;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa||vis[y]) continue;
gdis(y,x,dis+edge[i],from);
}
}
然后需要将 \(a\) 数组按 \(d\) 的大小来排序
bool cmp(int x,int y){
return d[x]<d[y];
}
最后利用双指针 \(l , r\),把任意两个出现的距离凑在一起，并判断可否凑出我们需要的 \(k\) 即可（注意复原的时候不要用 \(memset\) ，将 \(tot\) 清零即可)
void calc(int x){
tot=0,a[++tot]=x; //初始化
d[x]=0,b[x]=x;
for(int i=Head[x];i;i=Next[i]){ //遍历 x 的所有儿子
int y=to[i];
if(vis[y]) continue;
gdis(y,x,edge[i],y);
}
sort(a+1,a+1+tot,cmp); //排序
for(int i=1;i<=m;i++){
int l=1,r=tot;
if(ok[i]) continue;
while(l<r){
if(d[a[l]]+d[a[r]]>q[i]) r--; //当和比询问的长度大时,右指针左移
else if(d[a[l]]+d[a[r]]<q[i]) l++; //同上
else if(b[a[l]]==b[a[r]]){ //和为询问的长度,但同属一棵子树,继续下一种情况
if(d[a[r]]==d[a[r-1]]) r--;
else l++;
}else{
ok[i]=1;
break;
}
}
}
}
复杂度 \(\mathcal{O}(n \log^{2}n+n m\log n)\)
#include<bits/stdc++.h>
#define N 10005
using namespace std;
int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
} //快读
int Head[N],Next[N<<1],to[N<<1],edge[N<<1]; //链式前向星
bool vis[N],ok[N];
int n,m,tot,ctr,maxp[N];
int sz[N],q[N],a[N],b[N],d[N];
void add(int u,int v,int w){
to[++tot]=v,Next[tot]=Head[u],Head[u]=tot,edge[tot]=w;
}
bool cmp(int x,int y){
return d[x]<d[y];
}
void dfs(int x,int fa,int total){ //找重心
sz[x]=1,maxp[x]=0;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa||vis[y]) continue;
dfs(y,x,total);
sz[x]+=sz[y];
maxp[x]=max(maxp[x],sz[y]);
}
maxp[x]=max(maxp[x],total-sz[x]);
if(!ctr||maxp[x]<maxp[ctr]) ctr=x;
}
void gdis(int x,int fa,int dis,int from){
a[++tot]=x,d[x]=dis,b[x]=from;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa||vis[y]) continue;
gdis(y,x,dis+edge[i],from);
}
}
void calc(int x){
tot=0,a[++tot]=x;
d[x]=0,b[x]=x;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(vis[y]) continue;
gdis(y,x,edge[i],y);
}
sort(a+1,a+1+tot,cmp);
for(int i=1;i<=m;i++){
int l=1,r=tot;
if(ok[i]) continue;
while(l<r){
if(d[a[l]]+d[a[r]]>q[i]) r--;
else if(d[a[l]]+d[a[r]]<q[i]) l++;
else if(b[a[l]]==b[a[r]]){
if(d[a[r]]==d[a[r-1]]) r--;
else l++;
}else{
ok[i]=1;
break;
}
}
}
}
void solve(int x){
vis[x]=1,calc(x);
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(vis[y]) continue;
ctr=0,dfs(y,-1,sz[y]),dfs(ctr,-1,sz[y]);
solve(ctr);
}
}
int main(){
n=read(),m=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w),add(v,u,w);
}
dfs(1,-1,n),dfs(ctr,-1,n);
for(int i=1;i<=m;i++){
q[i]=read();
if(!q[i]) ok[i]=1; //特判
}
solve(ctr);
for(int i=1;i<=m;i++){
if(ok[i]) printf("AYE\n");
else printf("NAY\n");
}
return 0;
}
Ⅱ. P4178 Tree
题面要求小于等于 \(k\) 的路径数目，很自然的想到 点分治
这道题的统计答案与模板题不一样的地方是由等于 \(k\) 到小于等于 \(k\)
但是如果只是双指针统计的话，那么以下不合法的情况显然也会被算进答案：
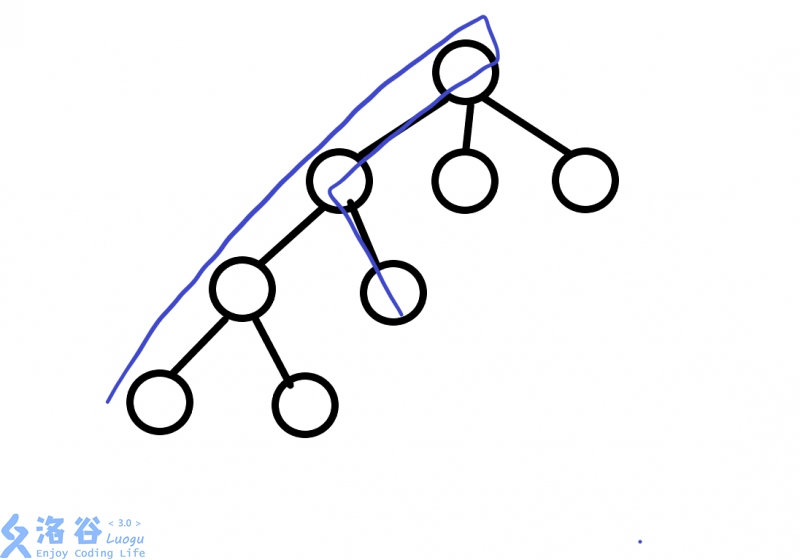
而我们需要的合法路径是长成这样的：
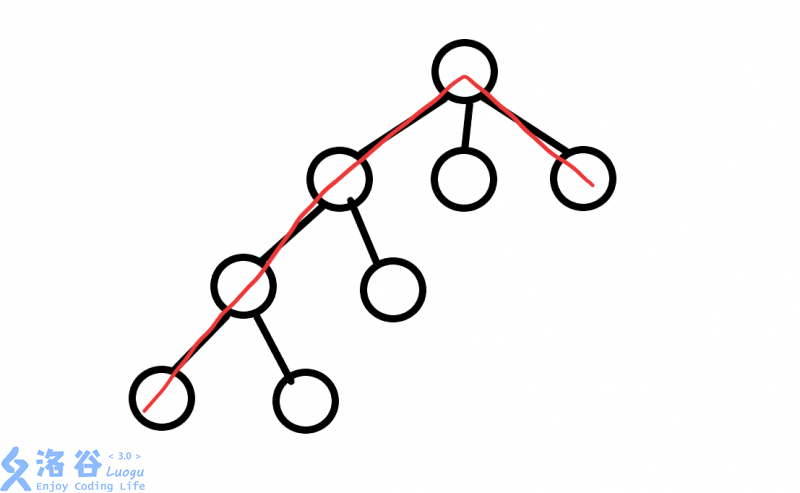
所以我们需要减去上述不合法的路径，怎么减呢？
不难发现，对于所有不合法的路径，都是在当前跟的某一棵子树上的（没有跨越两个子树）
所以我们可以对当前跟节点的每一条边进行遍历，利用容斥的思想减去不合法的路径。
具体操作为：当遍历重心节点的每一个儿子节点时，我们可以重新计算 \(dis\) ，然后把这个子树里符合条件的路径减掉（就是上述不合法路径），最后统计答案即可
#include<bits/stdc++.h>
#define N 40005
using namespace std;
int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,k,tot,root,ans;
int Head[N],to[N<<1],Next[N<<1],edge[N<<1];
int maxp[N],size[N],a[N],d[N];
bool vis[N];
void add(int u,int v,int w){
to[++tot]=v,Next[tot]=Head[u],Head[u]=tot,edge[tot]=w;
}
void dfs(int x,int fa,int total){
size[x]=1,maxp[x]=0;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(vis[y]||y==fa) continue;
dfs(y,x,total);
size[x]+=size[y],maxp[x]=max(maxp[x],size[y]);
}
maxp[x]=max(maxp[x],total-size[x]);
if(!root||maxp[x]<maxp[root]) root=x;
}
void get_dis(int x,int fa,int w){
d[++tot]=w;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa||vis[y]) continue;
get_dis(y,x,w+edge[i]);
}
}
int calc(int x,int w){
tot=0;
get_dis(x,-1,w);
sort(d+1,d+1+tot);
int l=1,r=tot,res=0;
while(l<r){
if(d[l]+d[r]<=k) res+=r-l,l++;
else r--;
}
return res;
}
void solve(int x){
vis[x]=1,ans+=calc(x,0);
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(vis[y]) continue;
ans-=calc(y,edge[i]); //减掉不合法路径
root=0,dfs(y,-1,size[y]),dfs(root,-1,size[y]);
solve(root);
}
}
int main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w),add(v,u,w);
}
k=read();
dfs(1,-1,n),dfs(root,-1,n);
solve(root);
printf("%d\n",ans);
return 0;
}
动态点分治
点分树可以看做是将整个点分治过程记录下来，将当前树的重心与上一层的树的重心连边（后者视作前者的父亲），这样就可以得到一个形态比较优秀的重构树，可以以比较优秀的复杂度解决不考虑树的形态的一类问题。
它是一棵 有根树，并且有很好的性质，最重要的一条是 树深不超过 \(O(logn)\)。这意味着我们可以 暴力跳父节点统计答案。
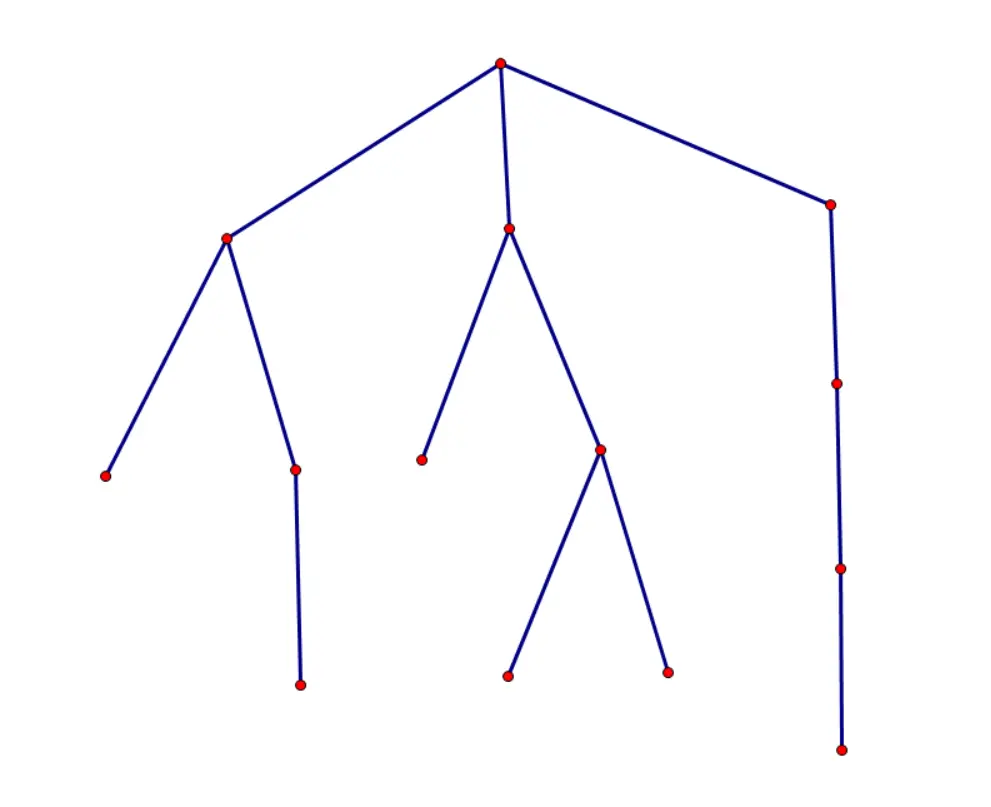
建出点分树来如下图所示：
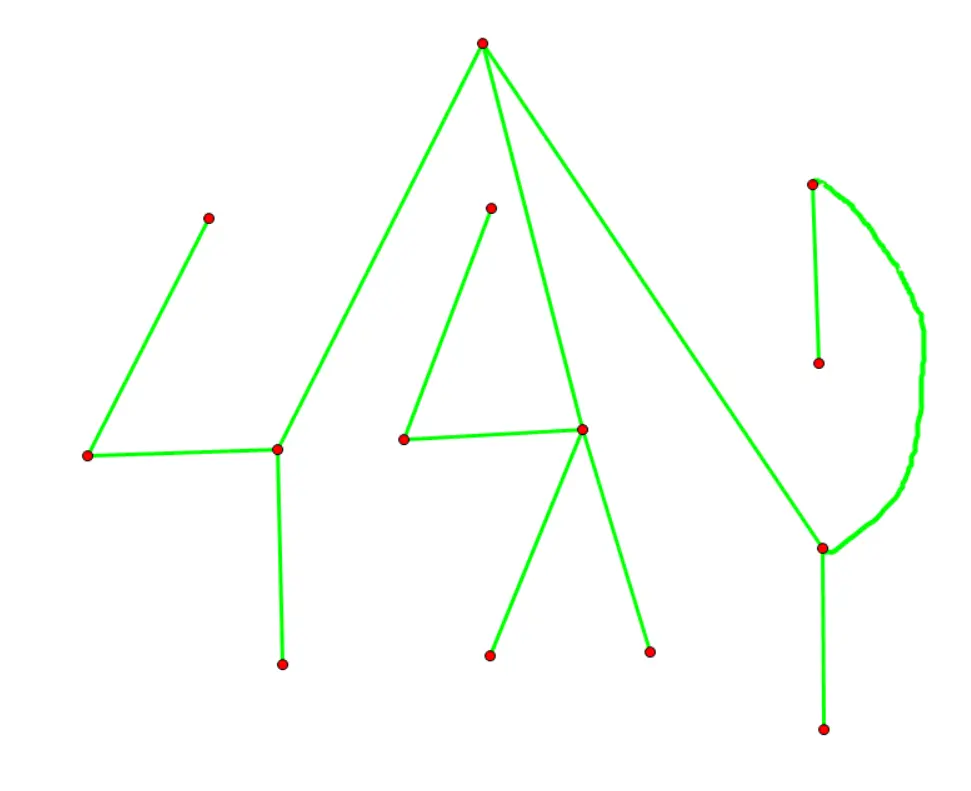
Ⅰ. P6329 【模板】点分树 | 震波
这道题要我们动态维护对于某个点距离小于 \(k\) 的点的权值和，这就是上述的典型的与树的形态无关的一类题目。
考虑一种暴力，每次询问都用点分治暴力求解，那么我们每次都找到重心统计答案即可。
可以发现，对于多次这样的询问，都进行了找重心的操作，但这是完全重复的，所以我们只用把对于每个重心的答案记录下来并查询即可。
我们具体地来看一看这个查询操作。
在点分治的过程中，我们会有一个数组 \(C\) 来记录对于这个点其子树内的点到它的每个距离对应的答案。
回忆一下点分治的做法，从整棵树的重心一步步地分治到当前节点。也就是说，从现在重构树的节点一直统计到当前节点。
这个是很好做的，我们只需要记录重构树的父子关系，计算当前节点答案需要经过的点即为重构树根节点到当前节点路径上的所有点。
那么我们再来考虑如何统计答案。
上面说到，要提出当前节点到重构树根节点的路径上的点，实际上就是从当前节点一直跳父亲，跳到根为止。
最开始在 \(x\) 的时候，直接将 $ x$ 子树的节点对 \(x\) 的贡献加入答案即可。再考虑在往上爬的过程中（设当前节点为 \(u\) ，与 \(x\) 的距离为 \(dis\) ），我们需要计算的是在 \(u\) 子树内但不在 \(x\) 子树内的节点对 \(x\) 的贡献，也就是在 \(u\) 子树但不在 \(x\) 子树的节点中与 \(x\) 的距离 \(≤y-dis\) 的节点的权值和。那么容斥一下可以得到，我们要求的就是与 \(u\) 子树内 \(u\) 距离 \(≤y-dis\) 的节点权值和减去 \(x\) 子树内与 \(u\) 距离 \(≤y-dis\) 的权值和。
容易发现，如果我们记 \(W_{i,j}\) 为 \(i\) 子树内与 \(i\) 的距离为 \(j\) 的节点权值和，那么我们每次询问的都是 \(W_i\) 的前缀和，那么我们就可以用树状数组来维护这些信息了。
摘自:https://www.luogu.com.cn/blog/_post/272378
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 4e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, m, tot, cnt, minn, rt, sum, ans;
int a[N], sz[N], ol[N << 1][21], lg[N << 1], fa[N], pos[N], d[N];
int Head[N], to[N], Next[N];
bool vis[N];
vector<int> C[2][N];
void add(int u, int v){
to[++tot] = v, Next[tot] = Head[u], Head[u] = tot;
}
void dfs0(int x, int f){
ol[++cnt][0] = x, pos[x] = cnt, d[x] = d[f] + 1;
for(int i = Head[x]; i; i = Next[i]){
int y = to[i]; if(y == f) continue;
dfs0(y, x), ol[++cnt][0] = x;
}
}
int get_min(int a, int b){
return d[a] < d[b] ? a : b;
}
void get_ol(){
for(int i = 2; i <= cnt; ++i) lg[i] = lg[i >> 1] + 1;
for(int t = 1; (1 << t) <= cnt; ++t)
for(int i = 1; i + (1 << t) <= cnt; ++i)
ol[i][t] = get_min(ol[i][t - 1], ol[i + (1 << t - 1)][t - 1]);
}
void find_rt(int x, int f){
sz[x] = 1; int res = 0;
for(int i = Head[x]; i; i = Next[i]){
int y = to[i]; if(y == f || vis[y]) continue;
find_rt(y, x); res = max(res, sz[y]), sz[x] += sz[y];
}
res = max(res, sum - sz[x]);
if(res < minn) minn = res, rt = x;
}
void dfs(int x){
vis[x] = 1, sz[x] = sum + 1;
C[0][x].resize(sz[x] + 1), C[1][x].resize(sz[x] + 1);
for(int i = Head[x]; i; i = Next[i]){
int y = to[i]; if(vis[y]) continue;
sum = sz[y], rt = 0, minn = INF;
find_rt(y, 0), fa[rt] = x;
dfs(rt);
}
}
void upd(int u, int opt, int x, int del){
++x; for(; x <= sz[u]; x += x & -x) C[opt][u][x] += del;
}
int qry(int u, int opt, int x){
int res = 0; x = min(x + 1, sz[u]);
for(; x; x -= x & -x) res += C[opt][u][x];
return res;
}
int get_dis(int x, int y){
if(pos[x] > pos[y]) swap(x, y);
int xx = pos[x], yy = pos[y], len = yy - xx + 1;
int lca = get_min(ol[xx][lg[len]], ol[yy - (1 << lg[len]) + 1][lg[len]]);
return d[x] + d[y] - d[lca] * 2;
}
void modify(int x, int w){
for(int i = x; i; i = fa[i]) upd(i, 0, get_dis(x, i), w);
for(int i = x; fa[i]; i = fa[i]) upd(i, 1, get_dis(x, fa[i]), w);
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i < n; ++i){
int u = read(), v = read();
add(u, v), add(v, u);
}
dfs0(1, 0), get_ol();
sum = n, minn = INF;
find_rt(1, 0), dfs(rt);
for(int i = 1; i <= n; ++i) modify(i, a[i]);
while(m--){
int opt = read(), x = read(), y = read();
x ^= ans, y ^= ans;
if(!opt){
ans = 0;
ans += qry(x, 0, y);
for(int i = x; fa[i]; i = fa[i]){
int dis = get_dis(x, fa[i]);
if(y >= dis) ans += qry(fa[i], 0, y - dis) - qry(i, 1, y - dis);
}
printf("%d\n", ans);
}else modify(x, y - a[x]), a[x] = y;
}
return 0;
}
性质与总结
- 性质：点分树深 \(O(logn)\) 级别。
- 性质：树上每个节点的度数不大于其在原树上的度数 +1。
- 对于每一道点分治问题，都需要注意如何避免合并 来自相同儿子的子树 的信息。
- 对于每一道点分树问题，都需要注意如何去掉每个节点与其父节点之间 重叠的贡献。
- 树上 点对 / 简单路径计数 可以考虑点分治。
- 技巧：对于统计可减信息的点分治，通常用子树内任意两个点对之间的贡献，减去每个儿子子树内任意两个点对之间的贡献。它们的统计方式相同，可以共用同一个函数减小码量。
例题
Ⅰ. P4075 [SDOI2016] 模式字符串
点分治，对于一个分治中心，使用哈希判断每个点是否能作为从该点到分治重心的一段前缀和后缀，再用桶统计即可。注意边界情况。
#include<bits/stdc++.h>
#define pb push_back
#define ull unsigned long long
#define ll long long
using namespace std;
const int N = 1e6 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int T, n, m, rt, ans;
ull pre[N], suf[N], pw[N];
char s[N], t[N];
vector<int> e[N], ori[N], rev[N];
int mx[N], sz[N], buc[N];
bool vis[N];
void find_rt(int x, int fa, int tot){
sz[x] = 1, mx[x] = 0;
for(int y : e[x]){
if(y == fa || vis[y]) continue;
find_rt(y, x, tot), sz[x] += sz[y];
mx[x] = max(mx[x], sz[y]);
}
mx[x] = max(mx[x], tot - sz[x]);
if(mx[x] < mx[rt]) rt = x;
}
ll calc(vector<int> &x, vector<int> &y){
ll res = 0;
for(int it : x) buc[(it - 1) % m + 1] ++;
for(int it : y) res += buc[m - (it - 1) % m];
for(int it : x) buc[(it - 1) % m + 1] --;
return res;
}
void find_val(int x, int fa, int dep, ull hsh, int anc){
hsh += s[x] * pw[dep - 1];
if(pre[dep] == hsh) ori[anc].pb(dep);
if(suf[dep] == hsh) rev[anc].pb(dep);
for(int y : e[x]){
if(vis[y] || y == fa) continue;
find_val(y, x, dep + 1, hsh, anc);
}
}
void divide(int x){
vis[x] = 1; ori[0].clear(), rev[0].clear();
if(s[x] == t[1]) ori[0].pb(1);
if(s[x] == t[m]) rev[0].pb(1);
for(int y : e[x]){
if(vis[y]) continue;
find_val(y, x, 2, s[x], y);
ans -= calc(ori[y], rev[y]);
for(int it : ori[y]) ori[0].pb(it);
for(int it : rev[y]) rev[0].pb(it);
ori[y].clear(), rev[y].clear();
}
ans += calc(ori[0], rev[0]);
for(int y : e[x]){
if(vis[y]) continue;
rt = 0, find_rt(y, x, sz[y]);
divide(rt);
}
}
void solve(){
n = read(), m = read();
scanf("%s", s + 1);
for(int i = 1; i <= n; ++i) e[i].clear();
for(int i = 1; i < n; ++i){
int u = read(), v = read();
e[u].pb(v), e[v].pb(u);
}
scanf("%s", t + 1);
for(int i = 1; i <= n; ++i) pre[i] = pre[i - 1] * 10007 + t[1 + (i - 1) % m];
for(int i = 1; i <= n; ++i) suf[i] = suf[i - 1] * 10007 + t[m - (i - 1) % m];
memset(vis, 0, sizeof(vis)); mx[0] = n, ans = 0;
find_rt(1, 0, n);
divide(rt);
printf("%d\n", ans);
return ;
}
int main(){
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
T = read();
for(int i = pw[0] = 1; i <= 1e6; ++i) pw[i] = pw[i - 1] * 10007;
while(T--) solve();
return 0;
}
Ⅱ.AT_cf17_final_j Tree MST
对于 MST 问题，我们每次选出一个边集求 MST，那么没有被选中的边也一定不会在最终的 MST 中，正确性显然。因此，只要我们选出的边集的并等于原图，并将所有边集的 MST 的并再求一次 MST，就能保证正确性。
对于每次分治重心 \(r\), 令 \(p_i = w_i + dis(i,r)\),我们每次选取 p 值最小的节点 i 与分治子树其它节点 j 连边，边权为 \(p_i+p_j\)。边的总数为$ O(nlogn)$，因此时间复杂度为 \(O(nlog^2n)\)。
#include<bits/stdc++.h>
#define pb push_back
#define ll long long
#define pll pair<ll, ll>
#define pii pair<int, int>
#define mp make_pair
using namespace std;
const int N = 2e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
ll ans;
int n, tot, rt, cnt;
int hd[N], to[N << 1], edge[N << 1], nxt[N << 1];
int a[N], sz[N], mx[N], fa[N];
bool vis[N];
vector<pll> c;
struct node{
int u, v;
ll w;
bool operator < (const node &A) const{return w < A.w;}
}g[N << 5];
void add(int u, int v, int w){
to[++tot] = v, nxt[tot] = hd[u], hd[u] = tot, edge[tot] = w;
}
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}
void find_rt(int x, int ff, int tot){
sz[x] = 1, mx[x] = 0;
for(int i = hd[x]; i; i = nxt[i]){
int y = to[i]; if(y == ff || vis[y]) continue;
find_rt(y, x, tot); sz[x] += sz[y];
mx[x] = max(mx[x], sz[y]);
}
mx[x] = max(mx[x], tot - sz[x]);
if(mx[x] < mx[rt]) rt = x;
}
void find_dis(int x, int ff, ll dis){
c.pb(mp(dis + a[x], x));
for(int i = hd[x]; i; i = nxt[i]){
int y = to[i]; if(vis[y] || y == ff) continue;
find_dis(y, x, dis + edge[i]);
}
}
void divide(int x){
vis[x] = 1, c.pb(mp(a[x], x));
for(int i = hd[x]; i; i = nxt[i]){
int y = to[i]; if(vis[y]) continue;
find_dis(y, x, edge[i]);
}
sort(c.begin(), c.end());
for(int i = 1; i < c.size(); ++i){
pll x = c[0], y = c[i];
g[++cnt] = (node){x.second, y.second, x.first + y.first};
}
c.clear();
for(int i = hd[x]; i; i = nxt[i]){
int y = to[i]; if(vis[y]) continue;
rt = 0, find_rt(y, x, sz[y]), divide(rt);
}
}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
n = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i < n; ++i){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, w);
}
mx[0] = n, find_rt(1, 0, n);
divide(rt);
for(int i = 1; i <= n; ++i) fa[i] = i;
sort(g + 1, g + 1 + cnt);
for(int i = 1; i <= cnt; ++i){
int x = g[i].u, y = g[i].v;
x = find(x), y = find(y);
if(x != y) ans += g[i].w, fa[x] = y;
}
printf("%lld\n", ans);
return 0;
}
Ⅲ. CF150E Freezing with Style
二分答案，将 \(≥m\) 的边视为 1，<m 的边视为 −1，点分治检查是否存在边权和 ≥0的路径。
\(l,r\)的限制提示我们使用单调队列。对于分治重心 \(R\)，计算儿子 \(v\) 的复杂度为 \(dv+maxd_w\)，其中 w 是已经处理的所有儿子，容易被卡到 \(n^2logn\)。
考虑启发式合并，按子树最大深度计算所有儿子可使 \(maxd_w\) 对复杂度不产生贡献。只需将所有儿子按照子树最大深度从小到大排序。原理其实也很简单，由于每次初始化的复杂度是在这个子树之前出现的路径的最大深度，由于所有子树已经排好序，因此最大深度就是这个子树的最大深度，那么初始化的总复杂度就是 \(O(\sum{mxdep})=O(\sum{siz})=O(n)\) 的了
时间复杂度 \(O(nlog^2n)\)。
#include<bits/stdc++.h>
#define pb push_back
#define pii pair<int, int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
const int N = 2e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
bool _u;
int n, L, R, rt, V, X, Y, ansx, ansy;
int sz[N], mx[N], mxd[N], w[N];
int f1[N], f2[N], ind1[N], ind2[N];
bool flag, vis[N];
vector<pii> e[N];
void find_rt(int x, int ff, int tot){
sz[x] = 1, mx[x] = 0;
for(auto y : e[x]){
if(y.fi == ff || vis[y.fi]) continue;
find_rt(y.fi, x, tot); sz[x] += sz[y.fi];
mx[x] = max(mx[x], sz[y.fi]);
}
mx[x] = max(mx[x], tot - sz[x]);
if(mx[x] < mx[rt]) rt = x;
}
void find_dep(int x, int ff){
mxd[x] = 1;
for(auto y : e[x]){
if(vis[y.fi] || y.fi == ff) continue;
find_dep(y.fi, x); mxd[x] = max(mxd[x], mxd[y.fi] + 1);
}
}
void find_val(int x, int ff, int dep, int val){
if(f2[dep] < val) f2[dep] = val, ind2[dep] = x;
for(auto y : e[x]){
if(vis[y.fi] || y.fi == ff) continue;
find_val(y.fi, x, dep + 1, val + (y.se >= V ? 1 : -1));
}
}
void divide(int x){
vis[x] = 1, ind1[0] = x;
find_dep(x, 0);
sort(e[x].begin(), e[x].end(), [&](pii x, pii y){return mxd[x.fi] < mxd[y.fi];});
int lim = 0;
for(auto y : e[x]){
if(vis[y.fi]) continue;
if(flag) break;
find_val(y.fi, x, 1, y.se >= V ? 1 : -1);
int cur = min(lim, R);
static int q[N];
int hd = 1, tl = 0;
for(int i = 1; i <= mxd[y.fi]; ++i){
while(cur >= 0 && cur + i >= L){
while(hd <= tl && f1[q[tl]] <= f1[cur]) tl--;
q[++tl] = cur;
--cur;
}
while(hd <= tl && q[hd] + i > R) ++hd;
if(hd <= tl){
int val = f1[q[hd]] + f2[i];
if(val >= 0) flag = 1, X = ind1[q[hd]], Y = ind2[i];
}
}
for(int i = 1; i <= mxd[y.fi]; ++i){
if(f2[i] > f1[i]) f1[i] = f2[i], ind1[i] = ind2[i];
f2[i] = -1e9;
}
lim = mxd[y.fi];
}
for(int i = 1; i <= mxd[x]; ++i) f1[i] = -1e9;
if(flag) return ;
for(auto y : e[x]){
if(flag) return ;
if(vis[y.fi]) continue;
rt = 0, find_rt(y.fi, x, sz[y.fi]);
divide(rt);
}
}
bool check(int mid){
V = mid, flag = 0;
memset(vis, 0, sizeof(vis));
rt = 0, find_rt(1, 0, n);
divide(rt);
return flag;
}
bool _v;
int main(){
cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
memset(f1, 0xcf, sizeof(f1)); f1[0] = 0;
memset(f2, 0xcf, sizeof(f2));
n = read(), L = read(), R = read(); mx[0] = n;
for(int i = 1; i < n; ++i){
int u = read(), v = read(); w[i] = read();
e[u].pb(mp(v, w[i])), e[v].pb(mp(u, w[i]));
}
sort(w + 1, w + n);
int l = 1, r = n - 1;
while(l <= r){
int mid = (l + r) >> 1;
if(check(w[mid])) ansx = X, ansy = Y, l = mid + 1;
else r = mid - 1;
}
printf("%d %d\n", ansx, ansy);
return 0;
}
