【做题记录】2023年6月
记录 6月份 做的题（好吧，还有一些五月的）。
5.29
Ⅰ.Starry Phase
\(a_i \le 2 ^ {16}\) ，所以可以将 \(a_i\) 分成前 8 位和后 8 位。
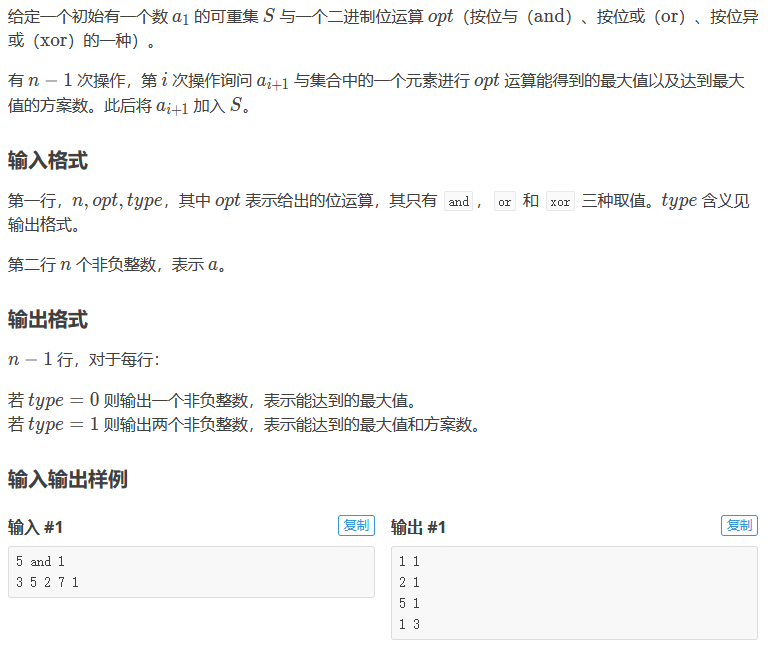
令 $f_{u,v} $ 表示 第一个数字前 8 位数字 \(u\) 和 第二个数字后 8 位数字 \(v\)，进行操作的最大值， \(g_{u,v}\) 表示个数，显然插入一个 \(a_i\) 就可以将 \(v \in [0 , 2 ^ 8 - 1]\) 的数字预处理出来。
那么对于每次要找的数字，可以枚举 和 它操作的数字的前 8 位数字，然后就解决了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 67, M = (1 << 8);
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, t;
char s[5];
int a[N], f[M][M], g[M][M];
void insert(int x){
int v = x >> 8; x &= (M - 1);
for(int i = 0; i < M; ++i){
int w = x;
if(s[1] == 'a') w &= i;
if(s[1] == 'o') w |= i;
if(s[1] == 'x') w ^= i;
if(f[v][i] < w) f[v][i] = w, g[v][i] = 1;
else if(f[v][i] == w) ++g[v][i];
}
}
signed main(){
n = read(), scanf("%s", s + 1), t = read();
for(int i = 1; i <= n; ++i) a[i] = read();
insert(a[1]);
for(int i = 2; i <= n; ++i){
int v = a[i] >> 8, vv = a[i] & (M - 1), mx = 0, mxn = 0;
for(int j = 0; j < M; ++j){
int val = 0;
if(!g[j][vv]) continue;
if(s[1] == 'a') val = ((v & j) << 8) + f[j][vv];
if(s[1] == 'o') val = ((v | j) << 8) + f[j][vv];
if(s[1] == 'x') val = ((v ^ j) << 8) + f[j][vv];
if(val > mx) mx = val, mxn = g[j][vv];
else if(val == mx) mxn += g[j][vv];
}
if(t) printf("%d %d\n", mx, mxn);
else printf("%d\n", mx);
insert(a[i]);
}
return 0;
}
5.30
Ⅰ. P2868 [USACO07DEC]Sightseeing Cows G
0/1 分数规划 最有比例环，近乎板题。
点击查看代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define ll long long
#define db double
#define eps 1e-5
using namespace std;
const int N = 5e3 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, m;
int tot, Head[N], to[N], Next[N], edge[N];
int a[N], in[N], vis[N], num[N];
db d[N];
void add(int u, int v, int w){
to[++tot] = v, Next[tot] = Head[u], Head[u] = tot, edge[tot] = w;
}
bool check(db r){
queue<int> q;
for(int i = 1; i <= n; ++i) q.push(i), d[i] = 0, vis[i] = num[i] = 0;
while(!q.empty()){
int x = q.front(); q.pop(), vis[x] = 0;
for(int i = Head[x]; i; i = Next[i]){
int y = to[i];
db dis = edge[i] * r - a[x];
if(d[y] > d[x] + dis){
d[y] = d[x] + dis;
if(!vis[y]){
q.push(y), vis[y] = 1;
if(++num[y] >= n) return true;
}
}
}
}
return false;
}
signed main(){
// freopen("1.in", "r", stdin);
n = read(), m = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= m; ++i){
int u = read(), v = read(), w = read();
add(u, v, w);
}
db l = 0, r = 1e3, ans = 0;
while(r - l > eps){
db mid = (l + r) / 2.0;
if(check(mid)) ans = mid, l = mid;
else r = mid;
}
printf("%.2lf\n", ans);
return 0;
}
6.8
Ⅰ. P2221 [HAOI2012]高速公路
Ⅱ. P4284 [SHOI2014] 概率充电器
树形 dp + 期望。
显然节点 \(i\) 通电有三种可能
1.它自己来电了
2.它的子树里有一个点来电了传了过来
3.它的子树外面有一个点来电了传了过来
两次 dfs 即可。
点击查看代码
#include<bits/stdc++.h>
#define db double
#define eps 1e-7
using namespace std;
const int N = 5e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n;
int tot, Head[N], to[N << 1], Next[N << 1], edge[N << 1];
int a[N];
db f[N], ans;
void add(int u, int v, int w){
to[++tot] = v, Next[tot] = Head[u], Head[u] = tot, edge[tot] = w;
}
void dfs1(int x, int fa){
for(int i = Head[x]; i; i = Next[i]){
int y = to[i]; if(y == fa) continue;
dfs1(y, x);
db pa = f[y] * (0.01 * edge[i]);
f[x] = f[x] + pa - f[x] * pa;
}
}
void dfs2(int x, int fa){
ans += f[x];
for(int i = Head[x]; i; i = Next[i]){
int y = to[i]; if(y == fa) continue;
db pb = f[y] * (0.01 * edge[i]);
if(pb + 1e-7 > 1.0 && pb - 1e-7 < 1.0){
dfs2(y, x); continue;
}
db pa = (f[x] - pb) / (1 - pb) * (0.01 * edge[i]);
f[y] = f[y] + pa - f[y] * pa;
dfs2(y, x);
}
}
signed main(){
n = read();
for(int i = 1; i < n; ++i){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, w);
}
for(int i = 1; i <= n; ++i) a[i] = read(), f[i] = a[i] * 0.01;
dfs1(1, 0), dfs2(1, 0);
printf("%.6lf\n", ans);
return 0;
}
Ⅲ. P2473 [SCOI2008] 奖励关
dp 式子不难想到，就是关于为什么要逆推，以下是我自己的理解：
1.首先顺推过来的话，因为求的是期望，我们要知道情况数，但由于有些情况是不存在的，所以情况数无法知道，所以只能逆推。
2.有后效性
点击查看代码
#include<bits/stdc++.h>
#define db double
using namespace std;
const int N = 1e2 + 67, M = (1 << 15) + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int K, n;
int p[N], sta[N];
db f[N][M];
signed main(){
K = read(), n = read();
for(int i = 1, x; i <= n; ++i){
p[i] = read();
while(x = read()) sta[i] |= (1 << x - 1);
}
for(int i = K; i; --i){
for(int j = 0; j < (1 << n); ++j){
for(int k = 1; k <= n; ++k)
if((j & sta[k]) == sta[k]) f[i][j] += max(f[i + 1][j], f[i + 1][j | (1 << k - 1)] + p[k]);
else f[i][j] += f[i + 1][j];
f[i][j] /= n;
}
}
printf("%.6lf\n", f[1][0]);
return 0;
}
Ⅳ. P3750 [六省联考 2017] 分手是祝愿
先求出至少需要按多少个灯。
显然每个灯最多按一次，且每一个灯按去的效果都是独一无二的，所以直接从大到小按就行了。
设 \(f_i\) 表示从 \(i + 1\) 个需要按的灯到 \(i\) 个需要按的灯的 按的次数的期望。
\[f[i] = \dfrac{i}{n} + \dfrac{n - i}{n} (f[i] + f[i + 1] + 1)
\]
\[f[i] = \dfrac{n + (n - i) \times f[i + 1]}{i}
\]
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e5 + 3, N = 1e5 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, k, cnt;
int a[N];
ll f[N];
ll qsm(ll a, int b){
ll res = 1;
for(; b; b >>= 1, a = a * a % mod) if(b & 1) res = res * a % mod;
return res;
}
signed main(){
n = read(), k = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = n; i; --i){
if(!a[i]) continue;
++cnt;
for(int j = 1; j * j <= i; ++j)
if(i % j == 0){
a[j] ^= 1;
if(j * j != i) a[i / j] ^= 1;
}
}
for(int i = n; i; --i){
ll tmp = ((ll)(n - i) * f[i + 1] + n) % mod;
tmp = tmp * qsm(i, mod - 2) % mod;
f[i] = tmp;
}
ll ans = 0;
if(cnt <= k) ans = cnt;
else{
for(int i = cnt; i > k; --i) ans = (ans + f[i]) % mod;
ans = (ans + k) % mod;
}
for(int i = 1; i <= n; ++i) ans = ans * i % mod;
printf("%lld\n", ans);
return 0;
}
Ⅴ. P3830 [SHOI2012]随机树
- 考虑第一问
设 \(g[i]\) 表示有 \(i\) 个叶子的二叉树的期望叶子平均深度。
则 \(i-1\) 个叶子的二叉树进行扩展后，叶节点数量变为 \(i\)，叶子深度之和增加\(2\)。
故有 \(g[i]=g[i-1]+2/i,g[1]=0\)。
即 \(\displaystyle\sum_{i=2}^n\displaystyle\frac{2}{i}.\)
-
考虑第二问
-
先证明一个小结论：设扩展\(i-1\)次后，左子树有 \(k\) 个叶子的概率、右子树有 \(i-k\) 个叶子的概率为 \(P(k)\)。则有 \(\forall k_1,k_2\in[1,i-1],P(k_1)=P(k_2)\)。
将扩展过程表示为序列，则其中 “扩展左子树” 有 \(k-1\) 个，“扩展右子树” 有 \(i-k-1\) 个，序列的形式数量为：
\[\displaystyle \binom{k-1+i-k-1}{k-1}=\displaystyle\frac{(i-2)!}{(k-1)!(i-k-1)!}.
\]
再考虑 \(k-1\) 次在左子树扩展形成的树的形态数，第 \(i\) 次可有 \(i\) 个叶节点可供扩展，故形态数为 \((k-1)!\)。
同理，右子树的形态数有 \((i-k-1)!\)。
故考虑扩展先后、树的形态，生成一个左子树有 \(k\) 个叶节点、右子树有 \(i-k\) 个叶节点的树的方案数为
\[\displaystyle\frac{(i-2)!}{(k-1)!(i-k-1)!} \cdot(k-1)!\cdot(i-k-1)!=(i-2)!
\]
与 \(k\) 无关，即 \(P(k_1)=P(k_2)\)。
- 前置芝士：整数概率公式
正整数随机变量 \(x\) 的期望值为：
\[E(x)=\sum_{i=1}^{\infty}P(x\geqslant i)
\]
证明：
\[E(x)=\sum_{i=1}^{\infty}P(x=i)\cdot i=\sum_{i=1}^{\infty}(P(x\geqslant i)-P(x\geqslant i+1))\cdot i \]
\[=\sum_{i=1}^{\infty}P(x\geqslant i)\cdot i-P(x\geqslant i)\cdot(i-1)=\sum_{i=1}^{\infty}P(x\geqslant i) \]
- 计算概率
设 \(f[i][j]\) 为树有 \(i\) 个叶节点，深度不小于 \(j\) 的概率，考虑枚举左子树叶节点数量为 \(k\)，有
\[\displaystyle f[i][j]=\displaystyle\frac{1}{i-1}\sum_{k=1}^{i-1}f[k][j-1]+f[i-k][j-1]-f[k][j-1]\cdot f[i-k][j-1]
\]
解释如下，首先考虑左、右子树深度不小于 \(j\) 的概率之和。再考虑左右子树深度皆大于等于 \(j\) 的情况计算了两次，减去一倍即可。
前文我们证明过，左子树叶节点数为 \(1,2,...,i-1\) 的概率相同，即均为 \(1/(i-1)\)。
初始条件，\(f[i][0]=1\)，因为无论有多少个叶子，深度大于等于 \(0\) 的概率总为 \(1\)。
由整数概率公式可知，期望深度 \(x\) 为：
\[E(x)=\sum_{i=1}^{\infty}P(x\geqslant i)=\sum_{i=1}^{n-1}f[n][i]\qquad(\forall x\geqslant n,P(x\geqslant i)=0).
\]
摘自 https://www.luogu.com.cn/blog/emptyset/solution-p3830
点击查看代码
#include<bits/stdc++.h>
#define db double
using namespace std;
const int N = 1e2 + 67;
int read(){
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
return x * f;
}
int opt, n;
db ans, f[N][N];
void solve1(){
for(int i = 2; i <= n; ++i) ans += 2.0 / i;
}
void solve2(){
for(int i = 1; i <= n; ++i) f[i][0] = 1;
for(int i = 2; i <= n; ++i)
for(int j = 1; j < i; ++j)
for(int k = 1; k < i; ++k)
f[i][j] += (f[k][j - 1] + f[i - k][j - 1] - f[k][j - 1] * f[i - k][j - 1]) / (i - 1);
for(int i = 1; i < n; ++i) ans += f[n][i];
}
signed main(){
opt = read(), n = read();
if(opt & 1) solve1();
else solve2();
printf("%.6lf\n", ans);
return 0;
}
