园龄：3年1个月粉丝：3 关注：4

📂学习笔记

🔖数论

2023-06-04 15:39阅读: 152评论: 0推荐: 0

*【学习笔记】(14) 初等数论（一）

1.【最大公约数（GCD）和最小公倍数（LCM）】

【基本性质、定理】

$g c d (a, b) = g c d (b, a - b) (a > b)$
$g c d (a, b) = g c d (b, a$ $m o d$ $b)$
$g c d (a, b)$ $l c m (a, b) = a b$

【推导结论】

$k | g c d (a, b) ⟺ k | a$ 且 $k | b$
$g c d (k, a b) = 1 ⟺ g c d (k, a) = 1$ 且 $g c d (k, b) = 1$
$(a + b) ∣ a b ⟹ g c d (a, b) \neq 1$
在斐波那契数列中求相邻两项的 $g c d$ 时，辗转相减次数等于辗转相除次数。
$g c d (F_{n}, F_{m}) = F_{g c d (n, m)}, F_{n} = F_{n - 1} + F_{n - 2}$

证明

$g c d (F_{n}, F_{n - 1}) = 1$
证明： $g c d (F_{n}, f_{n - 1}) = g c d (F_{n} - F_{n - 1}, F_{n - 1}) = g c d (F_{n - 2}, F_{n - 1}) = . . . = g c d (F_{0}, f_{1}) = 1$
$F_{n + m} = F_{n - 1} F_{m} + F_{n} F_{m + 1}$
对于 $m = 1$ 显然成立。
手推一下发现 $m = 2$ 也成立
用数学归纳法，若 $m = k - 1$ 和 $m = k$ 成立，那么 $m = k + 1$ 也成立：

F_{n + k + 1} = F_{n + k} + F_{n + k - 1}

= F_{n - 1} F_{k} + F_{n} F_{k + 1} + F_{n - 1} F_{k - 1} + F_{n} F_{k}

= F_{n - 1} (F_{k} + F_{k - 1}) + F_{n} (F_{k + 1} + F_{k})

= F_{n - 1} F_{k + 1} + F_{n} F_{k + 2}

$g c d (F_{n + m}, F_{n}) = g c d (F_{n}, F_{m})$
$g c d (F_{n + m}, F_{n}) = g c d (F_{n - 1} F_{m} + F_{n} F_{m + 1}, F_{n}) = g c d (F_{n - 1} F_{m}, F_{n}) = g c d (F_{m}, F_{n})$
$g c d (F_{n}, F_{m}) = F_{g c d (n, m)}$
结论3可以写作 $g c d (F_{n}, F_{m}) = g c d (F_{n - m}, F_{m})$ ，然后用辗转相减法归纳一下就好了。

2.费马小定理

$a^{p - 1} \equiv 1 (m o d p)$
引理：当 $p$ 是质数时，其因子只有 $1$ 和 $p$ 两个。因此，若两个数相乘是 $p$ 的倍数，其中必然至少有一个是 $p$ 的倍数。
当 $a$ 不是 $p$ 的倍数时，不存在 $x \neq y$ 且 $1 \leq x, y < p$ 使得 $x a \equiv y a (m o d p)$ 。因为据引理， $x - y$ 是 $p$ 的倍数，与 $1 \leq x, y < p$ 的限制矛盾。

进一步地，考虑 $1 \sim p - 1$ 所有数，它们乘以 $a$ 之后在模 $p$ 意义下的值互不相同，显然同上可以证明两两互不相同，说明仍得 $1 \sim p - 1$ 所有数。

因此， $\prod_{i = 1}^{p - 1} i \equiv \prod_{i = 1}^{p - 1} a i (m o d p)$ 。又因为 $\prod_{i = 1}^{p - 1} i$ 显然不是 $p$ 的倍数，所以两边消去

a^{p - 1} \equiv 1 (m o d p)

根据推导过程，它适用于 $p$ 是质数且 $a$ 不是 $p$ 的倍数的情形。

3.【裴蜀（Bézout）定理】

设 $a, b$ 是不全为零的整数，则存在整数 $x, y$ , 使得 $a x + b y = g c d (a, b)$
$g c d (a, b) | d ⟺ \exists x, y \in Z, a x + b y = d$

证明可以使用扩展欧几里得算法来证明

扩展欧几里得算法

扩展欧几里得算法简称扩欧或 exgcd。它是求解最大公约数的欧几里得算法的扩展，用于求解形如 $a x + b y = c$ 的二元线性不定方程。

1.1 解的存在性

先考虑一些较弱的结论。容易发现，无论 $x, y$ 的取值，左式一定是 $d = g c d (a, b)$ 的倍数。因此，当 $d ∤ c$ 时，方程显然无解。这使得我们可以为方程两侧同时除以 $d$ 。

同时，我们注意到为 $a$ 和 $b$ 同时除以 $d$ 之后， $a, b$ 互质。这说明我们将问题简化为求解 $a, b$ 互质时的情形。可见优先判断解的存在性的重要性。

根据直观感受，对于 $a ⊥ b$ ， $a x + b y$ 似乎能组合成任意一个整数，因为 $a, b$ 没有共同质因子。显然，只需证明 $a x m o d b$ 可以取到 $0 \sim b - 1$ 当中的任何一个数。

证明很容易，因为 $a ⊥ b$ 提供了很强的性质。实际上这是将费马小定理的证明中 $p$ 为质数的条件去掉了，换成了 $a ⊥ p$ ，本质并没有差别。

证明：考虑 $a x$ 和 $a y$ 满足 $0 \leq x, y < b$ 且 $x \neq y$ ，则 $a x \equiv̸ a y (m o d b)$ 。若存在，则 $a (x - y) \equiv 0 (m o d b)$ 。因为 $a ⊥ b$ ，所以 $x - y \equiv 0 (m o d b)$ （ $a$ 能够约去的原因是它不提供任何 $b$ 含有的质因子，也就是对使得 $a (x - y) \equiv 0 (m o d b)$ 成立没有任何贡献），这与 $0 \leq x, y < b$ 的限制矛盾。得证。

因为 $a x + b y$ 在 $a ⊥ b$ 时取遍所有整数，所以若 $d ∣ c$ ，方程就一定有解。

综上，我们得到了判断二元线性不定方程 $a x + b y = c$

存在解的充要条件： $g c d (a, b) ∣ c$ 。它被称为裴蜀定理或贝祖定理。

显然裴蜀定理可以推广到 $n$ 元的情况。 P4549 【模板】裴蜀定理

1.2 算法介绍

欲求解 $a x + b y = c$ ，设 $d = g c d (a, b)$ ，我们只需求解 $a x + b y = d$ ，并将解乘以 $c d$ 。根据裴蜀定理，方程的解必然在。

注意到等式右端等于 $x, y$ 前系数的最大公约数。回顾欧几里得算法（即辗转相除法），我们用到了关键结论 $g c d (a, b) = g c d (b, a m o d b)$ ，将问题缩至更小的规模上。利用这一思想，我们尝试将求解的方程也缩至更小的规模上。

exgcd 的核心思想与巧妙之处在于递归构造。假设我们已经得到了 $b x' + (a m o d b) y' = d$ 的一组解，则

a x + b y = b x' + (a m o d b) y'

= b x' + (a - b \times ⌊ \frac{a}{b} ⌋) y'

= a y' + b (x' - ⌊ \frac{a}{b} ⌋ y')

对比等式两端，有 $x = y' ， y = x' - ⌊ \frac{a}{b} ⌋ y'$ ，递归计算即可。

递归边界即当 $b = 0$ 时，根据辗转相除法，a=d。此时 $x = 1 ， y = 0$ 即为一组解。

上述过程即扩展欧几里得算法，时间复杂度与辗转相除相同。代码如下。

 void exgcd(int a, int b, int &x, int &y){
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}

【推导结论】

设不定方程 $a x + b y = g c d (a, b)$ 的一组特解为 ${\begin{cases} x = x_{0} \\ y = y_{0} \end{cases}$ ，则 $a x + b y = c (g c d (a, b) | c)$ 的通解为 ${\begin{cases} x = \frac{c}{g c d (a, b)} x_{0} + k \frac{b}{g c d (a, b)} \\ y = \frac{c}{g c d (a, b)} y_{0} - k \frac{a}{g c d (a, b)} \end{cases}$ $k \in Z$ 。 P5656 【模板】二元一次不定方程 (exgcd)
$\forall a, b, z \in N^{*}, g c d (a, b) = 1, \exists x, y \in N, a x + b y = a b - a - b + z$ P3951 [NOIP2017 提高组] 小凯的疑惑 / [蓝桥杯 2013 省] 买不到的数目

4.逆元

若 $a x \equiv 1 (m o d p)$ ，我们则称 x 为 a 在模 $p$ 下的逆元，记作 $x = i n v (a)$ 。

那逆元用来干什么呢？为了解决模意义下的除法问题，我们引入了逆元。inv(a) 其实可以看做模 $p$ 意义下的 $\frac{1}{a}$ ，那么在模 $p$ 意义下， $\frac{a}{b}$ 就可以变形为 $a \times i n v (a) (m o d p)$ 。

求逆元常规有以下三种方法：

4.1 费马小定理求逆元

根据费马小定理 $a^{p - 1} \equiv 1 (m o d p), g c d (a, p) = 1$ 。
那么 $a^{- 1} \equiv a^{p - 2} (m o d p)$ ,据此可快速幂求出一个数在模质数意义下的乘法逆元。

4.2 扩展欧几里得求逆元

$a x \equiv 1 (m o d p)$ 可以看成 $a x + b y = 1$ ，这样我们就可以使用扩展欧几里得的方法来解决啦。

从这个方法中我们可以发现， a 存在逆元的冲要条件是 $a ⊥ p$ 。

P1082 [NOIP2012 提高组] 同余方程

4.3 线性求逆元

如果我们要求 $n, p$ 求 $1 \sim n$ 中所有整数在模 $p$ 意义下的乘法逆元。
那么我们可以使用线性递推法。
假设 $1 \sim i - 1$ 的逆元已求得，那么，设 $p = i q + r$ ，即 $q = ⌊ \frac{p}{i} ⌋, r = p m o d i$ 。

i q + r \equiv 0 (m o d p)

i q \equiv - r (m o d p)

i \equiv \frac{- r}{q} (m o d p)

i \equiv - r \cdot i n v (q) (m o d p)

i n v (i) \equiv - i n v (r) \cdot q (m o d p)

i n v (i) \equiv (p - ⌊ \frac{p}{i} ⌋) \cdot i n v (p m o d i)

如果我们要求任意 n 个数 $a_{i} （ 1 \leq a_{i} < p ）$ 的逆元，设 $s$ 是 $a$ 的前缀积，那么可以先用费马求出 $s_{n}^{- 1}$ ，然后通过 $s_{i}^{- 1} = s_{i + 1}^{- 1} \times a_{i + 1}$ ，则 $a_{i}^{- 1} = s_{i - 1} \times s_{i}^{- 1}$ 。

P3811 【模板】乘法逆元

5.欧拉函数

5.1 定义与性质

欧拉函数定义为在 $[1, n]$ 中与 $n$ 互质的整数的个数，记作 $φ (n)$ 。

 int phi(int n){
	int res = n;
	for(int i = 2; i * i <= n; ++i){
		if(n % i == 0) res = res / i * (i - 1);
		while(n % i == 0) n /= i;
	}
	return n > 1 ? res / n * (n - 1) : res;
}

线性筛欧拉函数

根据性质6

 for(int i = 2; i <= 1e6; ++i){
	if(!v[i]) p[++tot] = i, phi[i] = i - 1, v[i] = i;
	for(int j = 1; j <= tot && i * p[j] <= 1e6; ++j){
		if(p[j] > v[i]) break;
		v[i * p[j]] = p[j];
		phi[i * p[j]] = phi[i] * (i % p[j] ? p[j] - 1 : p[j]);
	}
}

5.2 欧拉定理

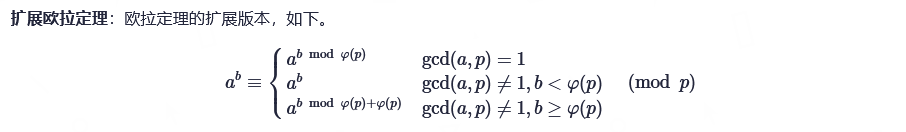
SP5971 LCMSUM - LCM Sum

点击查看代码

 #include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 51;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
int T, n, tot;
int ans[N], phi[N], p[N], v[N];
void solve(){
	phi[1] = 1;
	for(int i = 2; i <= 1e6; ++i){
		if(!v[i]) p[++tot] = i, phi[i] = i - 1, v[i] = i;
		for(int j = 1; j <= tot && i * p[j] <= 1e6; ++j){
			if(p[j] > v[i]) break;
			v[i * p[j]] = p[j];
			phi[i * p[j]] = phi[i] * (i % p[j] ? p[j] - 1 : p[j]);
		}
	}
	for(int i = 1; i <= 1e6; ++i)
		for(int j = 1; i * j <= 1e6; ++j)
			ans[i * j] += j * phi[j] / 2;
	for(int i = 1; i <= 1e6; ++i) ans[i] = i * ans[i] + i;
}
signed main(){
	T = read();
	solve();
	while(T--){
		n = read();
		printf("%lld\n", ans[n]);
	}
	return 0;
}

P4139 上帝与集合的正确用法

用欧拉定理缩指，发现一直递归下去 $φ (p)$ 会变成 1，而任何数 $m o d 1$ 都为 $0$ , 递归结束。

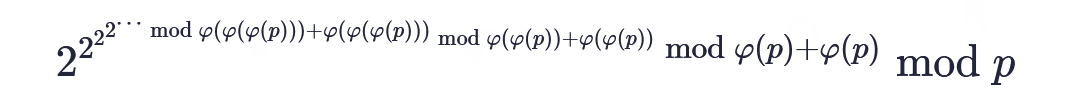
点击查看代码

 #include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e7 + 51;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
int T, p, tot;
int v[N], phi[N], pr[N];
void init(){
	phi[1] = 1;
	for(int i = 2; i <= 1e7; ++i){
		if(!v[i]) v[i] = i, phi[i] = i - 1, pr[++tot] = i;
		for(int j = 1; j <= tot && 1ll * pr[j] * i <= 1e7; ++j){
			if(pr[j] > v[i]) break;
			v[i * pr[j]] = pr[j];
			phi[i * pr[j]] = phi[i] * (i % pr[j] ? pr[j] - 1 : pr[j]);
		}
	}
} 
ll qsm(ll a, ll b, ll mod){
	int res = 1;
	for(; b; b >>= 1, a = (a * a) % mod) if(b & 1) res = (res * a) % mod;
	return res; 
} 
ll solve(int mod){
	if(mod == 1) return 0;
	return qsm(2, solve(phi[mod]) + phi[mod], mod);
}
int main(){
	init();
	T = read();
	while(T--){
		p = read();
		printf("%lld\n", solve(p));
	}
	return 0;
}

P3747 [六省联考 2017] 相逢是问候

和上题类似，使用光速幂。

点击查看代码

 #include<bits/stdc++.h>
#define ll long long
#define ls u << 1
#define rs u << 1 | 1
using namespace std;
const int N = 5e4 + 51, D = 60; 
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
int n, m, P, c, cntp;
int p[D];
int a[N][D], minn[N << 2];
ll sum[N << 2], c1[D][1 << 15], c2[D][1 << 15];
int phi(int x){
	int ans = x;
	for(int i = 2; i * i <= x; ++i){
		if(x % i) continue;
		while(x % i == 0) x /= i;
		ans = ans / i * (i - 1);
	}
	if(x > 1) ans = ans / x * (x - 1);
	return ans;
}
int mod(ll n, int p){
	return n >= p ? (n % p + p) : n;
}
void init(){
	for(int i = 0; i <= cntp; ++i){
		c1[i][0] = c2[i][0] = 1;
		for(int j = 1; j < 1 << 15; ++j) c1[i][j] = mod((ll) c1[i][j - 1] * c, p[i]);
		c2[i][1] = mod(c1[i][(1 << 15) - 1] * c, p[i]);
		for(int j = 2; j < 1 << 15; ++j) c2[i][j] = mod((ll) c2[i][j - 1] * c2[i][1], p[i]);
	}
}
int csm(int n, int i){
	return mod((ll) c1[i][n % (1 << 15)] * c2[i][n >> 15], p[i]);
}
int solve(int x, int cnt, int i){
	if(!cnt) return mod(x, p[i]);
	if(i == cntp) return 1;
	return csm(solve(x, cnt - 1, i + 1), i);
}
void PushUp(int u){
	minn[u] = min(minn[ls], minn[rs]);
	sum[u] = (sum[ls] + sum[rs]) % P;
}
void Build(int u, int l, int r){
	if(l == r) return minn[u] = 0, sum[u] = a[l][0], void();
	int mid = (l + r) >> 1;
	Build(ls, l, mid), Build(rs, mid + 1, r);
	PushUp(u);
}
void UpDate(int u, int l, int r, int L, int R){
	if(minn[u] > cntp) return ;
	if(l == r) return ++minn[u], sum[u] = a[l][minn[u]], void();
	int mid = (l + r) >> 1;
	if(L <= mid) UpDate(ls, l, mid, L, R);
	if(R > mid) UpDate(rs, mid + 1, r, L, R);
	PushUp(u);
} 
int Query(int u, int l, int r, int L, int R){
	if(L <= l && r <= R) return sum[u];
	int mid = (l + r) >> 1; ll ans = 0;
	if(L <= mid) ans = (ans + Query(ls, l, mid, L, R)) % P;
	if(R > mid) ans = (ans + Query(rs, mid + 1, r, L, R)) % P;
	return ans;
}
int main(){
	n = read(), m = read(), P = read(), c = read();
	p[cntp = 0] = P;
	while(p[cntp] > 1) ++cntp, p[cntp] = phi(p[cntp - 1]); 
	init();
	for(int i = 1; i <= n; ++i){
		a[i][0] = read();
		for(int j = 1; j <= cntp + 1; ++j) a[i][j] = solve(a[i][0], j, 0) % P;
		a[i][0] %= P;
	}
	Build(1, 1, n);
	while(m--){
		int opt = read(), l = read(), r = read();
		if(opt == 0) UpDate(1, 1, n, l, r);
		else printf("%d\n", Query(1, 1, n, l, r));
	}
	return 0;
}

6.离散对数问题

6.1 大步小步算法

 int BSGS(int a, int b, int p){
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	mp[b] = 0;
	for(int i = 1; i <= B; ++i) mp[(A = A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; ++i, AA = AA * A % p)
		if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
}

容易发现 BSGS 求得的是 $\log_{a} b$ 的最小的非负整数解，因为我们从小到大枚举指数。

6.2 扩展大步小步算法

P3846 [TJOI2007] 可爱的质数/【模板】BSGS

BSGS模板题。

点击查看代码

 #include<bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#define int long long 
using namespace std;
using namespace __gnu_pbds;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
	return x * f;
}
int p, b, m;
int BSGS(int a, int b, int p){
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	mp[b] = 0;
	for(int i = 1; i <= B; ++i) mp[(A = A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; ++i, AA = AA * A % p)
		if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
}
signed main(){
	p = read(), b = read(), m = read();
	int ans = BSGS(b, m, p);
	if(~ans) printf("%d\n", ans);
	else printf("no solution\n");
	return 0;
}

P4195 【模板】扩展 BSGS/exBSGS

exBSGS模板题

点击查看代码

 #include<bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#define int long long 
using namespace std;
using namespace __gnu_pbds;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
	return x * f;
}
int a, b, p;
int BSGS(int a, int b, int p){
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	mp[b] = 0;
	for(int i = 1; i <= B; ++i) mp[(A = A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; ++i, AA = AA * A % p)
		if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
}
void exgcd(int a, int b, int &x, int &y){
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int inv(int x, int p){
	return exgcd(x, p, x, *new int), (x % p + p) % p;
}
int exBSGS(int a, int b, int p){
	int d = __gcd(a, p), cnt = 0;
	a %= p, b %= p;
	while(d > 1){
		if(b == 1) return cnt;
		if(b % d) return -1;
		p /= d, b = b / d * inv(a / d, p) % p;
		d = __gcd(p, a %= p), ++cnt;
	}
	int ans = BSGS(a, b, p);
	return ~ans ? ans + cnt : -1;
}
signed main(){
	while(1){
		a = read(), p = read(), b = read();
		if(!p) break;
		int ans = exBSGS(a, b, p);
		if(~ans) printf("%d\n", ans);
		else printf("No Solution\n");
	}
	return 0;
}

7.线性同余方程组

7.1 中国剩余定理

7.2 扩展中国剩余定理

P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

点击查看代码

 #include<bits/stdc++.h>
#define N 15
#define int long long
using namespace std;
int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
int n,M=1,X;
int a[N],b[N],m[N];
void exgcd(int a,int b,int &x,int &y){
	if(b==0){
		x=1,y=0;
		return ;
	}
	exgcd(b,a%b,y,x);
	y-=(a/b)*x;
}
signed main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read(),b[i]=read();
		M*=a[i];
	} 
	for(int i=1;i<=n;i++){
		m[i]=M/a[i];
		int x=0,y=0;
		exgcd(m[i],a[i],x,y);
		X+=b[i]*m[i]*((x%a[i]+a[i])%a[i]);
	}
	printf("%lld\n",X%M);
	return 0;
}

P4777 【模板】扩展中国剩余定理（EXCRT）

点击查看代码

 #include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 51;
ll read(){
	ll x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
}
ll n, a, b, c, d;
void exgcd(ll a, ll b, ll &x, ll &y){
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
}
int main(){
	n = read(), a = read(), b = read();
	for(int i = 1; i < n; ++i){
		c = read(), d = read();
		ll e = __gcd(a, c), f = (d - b % c + c) % c, inv;
		c /= e, f /= e;
		exgcd(a / e, c, inv, *new long long), inv = (inv % c + c) %c;
		b += (__int128) f * inv % c * a, a *= c, b %= a;
	}
	printf("%lld\n", b);
	return 0;
}

8.高斯消元法

8.1过程

首先要把方程转化为增广矩阵

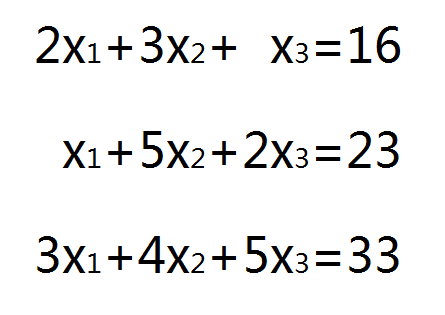
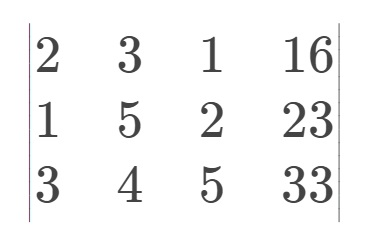
模板 P3389 【模板】高斯消元法

高斯消元

首先找到一个第一列的数不为0的行（一般找第一列的数最大的行）（如果都为0就跳过当前步）

然后用它的第一列的数将下面行当前列的值化为0，变换过的初等矩阵与原矩阵等价，化为方程后依然成立

本矩阵第一列的数最大的为第三行就把第三行与第一行交换

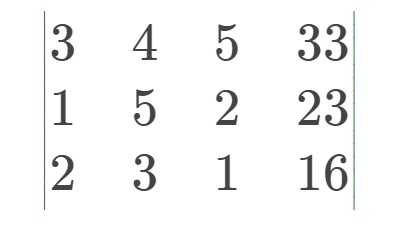
然后将下面行的当前列消去，如图

最后得到上三角矩阵如图

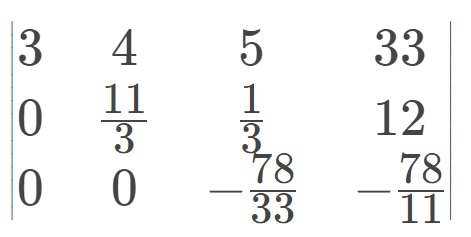
这样可以解出 $a_{3}$ 的值然后会带之后解出 $a_{2}$ 的值，依此类推。

 #include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int, int>
#define ls u << 1
#define rs u << 1 | 1
#define eps 1e-7
#define db double
using namespace std;
const int N = 1e2 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f; 
}
 
bool _u;
 
int n;
db a[N][N], ans[N];
 
int solve(int n){
	int r, c = 1;
	for(r = 1; r <= n && c <= n; ++r, ++c){
		int maxn = r;
		for(int i = r; i <= n; ++i) if(fabs(a[i][c]) > fabs(a[maxn][c])) maxn = i;
		if(maxn != r) swap(a[r], a[maxn]);
		if(fabs(a[r][c]) < eps){--r; continue;}
		for(int i = r + 1; i <= n; ++i){
			if(fabs(a[i][c]) > eps){
				db tmp = a[i][c] / a[r][c];
				for(int j = c; j <= n + 1; ++j) a[i][j] -= a[r][j] * tmp;
				a[i][c] = 0;
			} 
		}
	}
	for(int i = r; i <= n; ++i) if(fabs(a[i][c]) > eps) return -1;
	if(r <= n) return n - r + 1;
	for(int i = n; i; --i){
		for(int j = i + 1; j <= n; ++j) a[i][n + 1] -= a[i][j] * ans[j];
		ans[i] = a[i][n + 1] / a[i][i];
	}
	return 0;
}
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read();
	for(int i = 1; i <= n; ++i) for(int j = 1; j <= n + 1; ++j) scanf("%lf", &a[i][j]);
	int flag = solve(n);
	if(flag != 0) printf("No Solution\n");
	else for(int i = 1; i <= n; ++i) printf("%.2lf\n", ans[i]);
	return 0;
}

高斯约旦消元

同高斯消元大体差不多，但消元时上面计算过的行也要消去当前列，最后得到的是对角矩阵而不是上三角矩阵。

第一次和高斯消元相同

然后第二次要将第一行的也消去

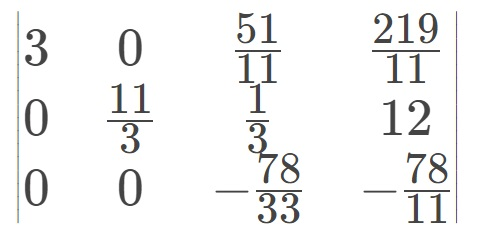
最后得到的如图

 #include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int, int>
#define ls u << 1
#define rs u << 1 | 1
#define eps 1e-7
#define db double
using namespace std;
const int N = 1e2 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f; 
}
 
bool _u;
 
int n;
db a[N][N];
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read();
	for(int i = 1; i <= n; ++i) for(int j = 1; j <= n + 1; ++j) scanf("%lf", &a[i][j]);
	for(int i = 1; i <= n; ++i){
		int r = i;
		for(int j = i + 1; j <= n; ++j) if(fabs(a[j][i]) > fabs(a[r][i])) r = j;
		if(fabs(a[r][i]) < eps) printf("No Solution\n"), exit(0);
		for(int j = 1; j <= n + 1; ++j) swap(a[i][j], a[r][j]);
		for(int j = 1; j <= n; ++j){
			if(j == i) continue;
			db tmp = a[j][i] / a[i][i];
			for(int k = i + 1; k <= n + 1; ++k) a[j][k] -= a[i][k] * tmp;
		}
	}
	for(int i = 1; i <= n; ++i) printf("%.2lf\n", a[i][n + 1] / a[i][i]);
	return 0;
}

P4035 [JSOI2008] 球形空间产生器
一个球体上的所有点到球心距离相等，因此我们只需求出一个点（ $x_{1}, x_{2}, x_{3} \dots \dots x_{n}$ ），使得：
$\sum_{j = 1}^{n} (a_{i, j} - x_{j})^{2} = C$
其中C为常数， $a_{i, j}$ 是点的坐标。
改方程组由 $n + 1$ 个 $n$ 元二次方程构成，当然不是线性的，怎么办呢？
我们可以通过相邻两个方程做差，变成 $n$ 个 $n$ 元一次方程组，消去常数C
有点像数学中数列求通项公式或者前 $n$ 项和
于是有：

$\sum_{j = 1}^{n} (a_{i, j}^{2} - a_{i + 1, j}^{2} - 2 x_{j} (a_{i, j} - a_{i + 1, j})) = 0$
把变量放左边，常数放右边：
$\sum_{j = 1}^{n} 2 (a_{i, j} - a_{i + 1, j}) x_{j} = \sum_{j = 1}^{n} (a_{i, j}^{2} - a_{i + 1, j}^{2}) (i = 1, 2, 3, . . ., n)$

so,我们要对这个增广矩阵进行高斯消元：

  
#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int, int>
#define ls u << 1
#define rs u << 1 | 1
#define eps 1e-7
#define db double
using namespace std;
const int N = 1e2 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f; 
}
 
bool _u;
 
int n;
db b[N][N];
db a[N][N];
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read();
	for(int i = 1; i <= n + 1; ++i) for(int j = 1; j <= n; ++j) scanf("%lf", &b[i][j]);
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= n; ++j){
			a[i][j] = 2 * (b[i][j] - b[i + 1][j]);
			a[i][n + 1] += b[i][j] * b[i][j] - b[i + 1][j] * b[i + 1][j];
		}
 	}
	for(int i = 1; i <= n; ++i){
		int r = i;
		for(int j = i + 1; j <= n; ++j) if(fabs(a[j][i]) > fabs(a[r][i])) r = j;
		for(int j = 1; j <= n + 1; ++j) swap(a[i][j], a[r][j]);
		for(int j = 1; j <= n; ++j){
			if(j == i) continue;
			db tmp = a[j][i] / a[i][i];
			for(int k = i + 1; k <= n + 1; ++k) a[j][k] -= a[i][k] * tmp;
		}
	}
	for(int i = 1; i <= n; ++i) printf("%.3lf ", a[i][n + 1] / a[i][i]);
	return 0;
}

8.2 比较

约旦法精度更好、代码更简单，没有回带的过程。

但约旦法无法分辨无解与无唯一解的情况。

对于高斯消元法：

如果有一行方程的所有变量的系数都为0，而常数项不为0，方程当然就无解啦。
如果有一行方程的所有变量的系数都为0，常数项也为0，那么这就说明出现了自由元（就是在这个方程中不受约束可以自由取值的未知数），且自由元的个数=全部为0的行数，这样就会导致方程多解了。

8.3 应用

8.3.1 解异或方程组

P2962 [USACO09NOV] Lights G

对于一个灯只有按或者不按两种状态，如果按也只会按一次，最终我们希望所有的灯的状态都为 $1$ ，那么对于每一个灯 $i$ 的状态就是与它相连的每一个灯包括它自己按或者不按的状态 $d [i]$ 的异或和

(a [1] [i] \times d [1]) x o r (a [2] [i] \times d [2]) x o r \dots x o r (a [n] [i] \times d [n]) = 1

即解这 $n$ 个异或方程组。

类似于高斯消元解线性方程组，我们同样要将一些系数消为 0 。发现系数 $(\in 0, 1)$ 。
考虑高斯消元的过程，因为我们选取的那一行的那一列的系数必然为 $1$ ，所以我们对于系数同样为 1 的那一行相异或一下即可。发现系数的变换是可行的。

举个例子：

$1 \times x 1$ xor $0 \times x 2$ xor $1 \times x 3 = 1$
$1 \times x 1$ xor $1 \times x 2$ xor $0 \times x 3 = 1$
得:

$0 \times x 1$ xor $1 \times x 2$ xor $1 \times x 3 = 0$

所以把减消元改为异或消元即可。

对于这道题，因为有自由元（即不确定的 x），我们需要 dfs 选取最优解。

 #include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pii pair<int, int>
#define ls u << 1
#define rs u << 1 | 1
#define eps 1e-7
#define db double
using namespace std;
const int N = 1e2 + 67;
int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f; 
}
 
bool _u;
 
int n, m, ans = 67;
int a[N][N], l[N];
 
int solve(int n){
	bool flag = 1;
	for(int i = 1; i <= n; ++i){
		int r = i;
		for(int j = i + 1; j <= n; ++j) if(a[j][i] > a[r][i]) r = j;
		if(!a[r][i]){flag = 0; continue;}
		swap(a[i], a[r]);
		for(int j = 1; j <= n; ++j){
			if(i == j || !a[j][i]) continue;
			for(int k = i; k <= n + 1; ++k) a[j][k] ^= a[i][k];
		}
	}
	return flag;
}
 
void dfs(int x, int num){
	if(num >= ans) return ;
	if(x == 0) return ans = num, void();
	if(a[x][x]){
		bool v = a[x][n + 1];
		for(int i = x + 1; i <= n; ++i) if(a[x][i]) v ^= l[i];
		dfs(x - 1, num += (l[x] = v));
	}else{
		l[x] = 0, dfs(x - 1, num);
		l[x] = 1, dfs(x - 1, num + 1);
	}
}
 
bool _v;
 
int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";
	
	n = read(), m = read();
	for(int i = 1; i <= n; ++i) a[i][i] = 1, a[i][n + 1] = 1;
	for(int i = 1, x, y; i <= m; ++i) x = read(), y = read(), a[x][y] = a[y][x] = 1;
	int flag = solve(n);
	if(flag){
		int res = 0;
		for(int i = 1; i <= n; ++i)  res += a[i][n + 1];
		printf("%d\n", res);
	}else dfs(n, 0), printf("%d\n", ans);
	return 0;
}

参考:
https://mzwuzad.blog.luogu.org/noip-2017-xiao-kai-di-ni-huo
https://www.cnblogs.com/alex-wei/p/Number_Theory.html
https://www.cnblogs.com/Xing-Ling/p/11990652.html

上一篇【题解】 P5904 [POI2014]HOT-Hotels 加强版

下一篇*【学习笔记】(18) 长链剖分

本文作者：南风未起

本文链接：https://www.cnblogs.com/jiangchen4122/p/17417678.html

posted @ 2023-06-04 15:39 Aurora-JC 阅读(152) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

	void exgcd(int a, int b, int &x, int &y){
	if(!b) return x = 1, y = 0, void();
	exgcd(b, a % b, y, x), y -= a / b * x;
	}

	int phi(int n){
	int res = n;
	for(int i = 2; i * i <= n; ++i){
	if(n % i == 0) res = res / i * (i - 1);
	while(n % i == 0) n /= i;
	}
	return n > 1 ? res / n * (n - 1) : res;
	}

	for(int i = 2; i <= 1e6; ++i){
	if(!v[i]) p[++tot] = i, phi[i] = i - 1, v[i] = i;
	for(int j = 1; j <= tot && i * p[j] <= 1e6; ++j){
	if(p[j] > v[i]) break;
	v[i * p[j]] = p[j];
	phi[i * p[j]] = phi[i] * (i % p[j] ? p[j] - 1 : p[j]);
	}
	}

	#include<bits/stdc++.h>
	#define int long long
	using namespace std;
	const int N = 1e6 + 51;
	int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' \|\| ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
	}
	int T, n, tot;
	int ans[N], phi[N], p[N], v[N];
	void solve(){
	phi[1] = 1;
	for(int i = 2; i <= 1e6; ++i){
	if(!v[i]) p[++tot] = i, phi[i] = i - 1, v[i] = i;
	for(int j = 1; j <= tot && i * p[j] <= 1e6; ++j){
	if(p[j] > v[i]) break;
	v[i * p[j]] = p[j];
	phi[i * p[j]] = phi[i] * (i % p[j] ? p[j] - 1 : p[j]);
	}
	}
	for(int i = 1; i <= 1e6; ++i)
	for(int j = 1; i * j <= 1e6; ++j)
	ans[i * j] += j * phi[j] / 2;
	for(int i = 1; i <= 1e6; ++i) ans[i] = i * ans[i] + i;
	}
	signed main(){
	T = read();
	solve();
	while(T--){
	n = read();
	printf("%lld\n", ans[n]);
	}
	return 0;
	}

	#include<bits/stdc++.h>
	#define ll long long
	using namespace std;
	const int N = 1e7 + 51;
	int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' \|\| ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
	}
	int T, p, tot;
	int v[N], phi[N], pr[N];
	void init(){
	phi[1] = 1;
	for(int i = 2; i <= 1e7; ++i){
	if(!v[i]) v[i] = i, phi[i] = i - 1, pr[++tot] = i;
	for(int j = 1; j <= tot && 1ll * pr[j] * i <= 1e7; ++j){
	if(pr[j] > v[i]) break;
	v[i * pr[j]] = pr[j];
	phi[i * pr[j]] = phi[i] * (i % pr[j] ? pr[j] - 1 : pr[j]);
	}
	}
	}
	ll qsm(ll a, ll b, ll mod){
	int res = 1;
	for(; b; b >>= 1, a = (a * a) % mod) if(b & 1) res = (res * a) % mod;
	return res;
	}
	ll solve(int mod){
	if(mod == 1) return 0;
	return qsm(2, solve(phi[mod]) + phi[mod], mod);
	}
	int main(){
	init();
	T = read();
	while(T--){
	p = read();
	printf("%lld\n", solve(p));
	}
	return 0;
	}

	#include<bits/stdc++.h>
	#define ll long long
	#define ls u << 1
	#define rs u << 1 \| 1
	using namespace std;
	const int N = 5e4 + 51, D = 60;
	int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' \|\| ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
	}
	int n, m, P, c, cntp;
	int p[D];
	int a[N][D], minn[N << 2];
	ll sum[N << 2], c1[D][1 << 15], c2[D][1 << 15];
	int phi(int x){
	int ans = x;
	for(int i = 2; i * i <= x; ++i){
	if(x % i) continue;
	while(x % i == 0) x /= i;
	ans = ans / i * (i - 1);
	}
	if(x > 1) ans = ans / x * (x - 1);
	return ans;
	}
	int mod(ll n, int p){
	return n >= p ? (n % p + p) : n;
	}
	void init(){
	for(int i = 0; i <= cntp; ++i){
	c1[i][0] = c2[i][0] = 1;
	for(int j = 1; j < 1 << 15; ++j) c1[i][j] = mod((ll) c1[i][j - 1] * c, p[i]);
	c2[i][1] = mod(c1[i][(1 << 15) - 1] * c, p[i]);
	for(int j = 2; j < 1 << 15; ++j) c2[i][j] = mod((ll) c2[i][j - 1] * c2[i][1], p[i]);
	}
	}
	int csm(int n, int i){
	return mod((ll) c1[i][n % (1 << 15)] * c2[i][n >> 15], p[i]);
	}
	int solve(int x, int cnt, int i){
	if(!cnt) return mod(x, p[i]);
	if(i == cntp) return 1;
	return csm(solve(x, cnt - 1, i + 1), i);
	}
	void PushUp(int u){
	minn[u] = min(minn[ls], minn[rs]);
	sum[u] = (sum[ls] + sum[rs]) % P;
	}
	void Build(int u, int l, int r){
	if(l == r) return minn[u] = 0, sum[u] = a[l][0], void();
	int mid = (l + r) >> 1;
	Build(ls, l, mid), Build(rs, mid + 1, r);
	PushUp(u);
	}
	void UpDate(int u, int l, int r, int L, int R){
	if(minn[u] > cntp) return ;
	if(l == r) return ++minn[u], sum[u] = a[l][minn[u]], void();
	int mid = (l + r) >> 1;
	if(L <= mid) UpDate(ls, l, mid, L, R);
	if(R > mid) UpDate(rs, mid + 1, r, L, R);
	PushUp(u);
	}
	int Query(int u, int l, int r, int L, int R){
	if(L <= l && r <= R) return sum[u];
	int mid = (l + r) >> 1; ll ans = 0;
	if(L <= mid) ans = (ans + Query(ls, l, mid, L, R)) % P;
	if(R > mid) ans = (ans + Query(rs, mid + 1, r, L, R)) % P;
	return ans;
	}
	int main(){
	n = read(), m = read(), P = read(), c = read();
	p[cntp = 0] = P;
	while(p[cntp] > 1) ++cntp, p[cntp] = phi(p[cntp - 1]);
	init();
	for(int i = 1; i <= n; ++i){
	a[i][0] = read();
	for(int j = 1; j <= cntp + 1; ++j) a[i][j] = solve(a[i][0], j, 0) % P;
	a[i][0] %= P;
	}
	Build(1, 1, n);
	while(m--){
	int opt = read(), l = read(), r = read();
	if(opt == 0) UpDate(1, 1, n, l, r);
	else printf("%d\n", Query(1, 1, n, l, r));
	}
	return 0;
	}

	int BSGS(int a, int b, int p){
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	mp[b] = 0;
	for(int i = 1; i <= B; ++i) mp[(A = A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; ++i, AA = AA * A % p)
	if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
	}

	#include<bits/stdc++.h>
	#include <ext/pb_ds/assoc_container.hpp>
	#define int long long
	using namespace std;
	using namespace __gnu_pbds;
	int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' \|\| ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
	return x * f;
	}
	int p, b, m;
	int BSGS(int a, int b, int p){
	int A = 1, B = sqrt(p) + 1; a %= p, b %= p;
	gp_hash_table <int, int> mp;
	mp[b] = 0;
	for(int i = 1; i <= B; ++i) mp[(A = A * a % p) * b % p] = i;
	for(int i = 1, AA = A; i <= B; ++i, AA = AA * A % p)
	if(mp.find(AA) != mp.end()) return i * B - mp[AA];
	return -1;
	}
	signed main(){
	p = read(), b = read(), m = read();
	int ans = BSGS(b, m, p);
	if(~ans) printf("%d\n", ans);
	else printf("no solution\n");
	return 0;
	}

	#include<bits/stdc++.h>
	#define N 15
	#define int long long
	using namespace std;
	int read(){
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'\|\|ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
	}
	int n,M=1,X;
	int a[N],b[N],m[N];
	void exgcd(int a,int b,int &x,int &y){
	if(b==0){
	x=1,y=0;
	return ;
	}
	exgcd(b,a%b,y,x);
	y-=(a/b)*x;
	}
	signed main(){
	n=read();
	for(int i=1;i<=n;i++){
	a[i]=read(),b[i]=read();
	M*=a[i];
	}
	for(int i=1;i<=n;i++){
	m[i]=M/a[i];
	int x=0,y=0;
	exgcd(m[i],a[i],x,y);
	X+=b[i]m[i]((x%a[i]+a[i])%a[i]);
	}
	printf("%lld\n",X%M);
	return 0;
	}

	#include<bits/stdc++.h>
	#define fi first
	#define se second
	#define mp make_pair
	#define pii pair<int, int>
	#define ls u << 1
	#define rs u << 1 \| 1
	#define eps 1e-7
	#define db double
	using namespace std;
	const int N = 1e2 + 67;
	int read(){
	int x = 0, f = 1; char ch = getchar();
	while(ch < '0' \|\| ch > '9'){if(ch == '-') f = -f; ch = getchar();}
	while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
	return x * f;
	}

	bool _u;

	int n;
	db a[N][N], ans[N];

	int solve(int n){
	int r, c = 1;
	for(r = 1; r <= n && c <= n; ++r, ++c){
	int maxn = r;
	for(int i = r; i <= n; ++i) if(fabs(a[i][c]) > fabs(a[maxn][c])) maxn = i;
	if(maxn != r) swap(a[r], a[maxn]);
	if(fabs(a[r][c]) < eps){--r; continue;}
	for(int i = r + 1; i <= n; ++i){
	if(fabs(a[i][c]) > eps){
	db tmp = a[i][c] / a[r][c];
	for(int j = c; j <= n + 1; ++j) a[i][j] -= a[r][j] * tmp;
	a[i][c] = 0;
	}
	}
	}
	for(int i = r; i <= n; ++i) if(fabs(a[i][c]) > eps) return -1;
	if(r <= n) return n - r + 1;
	for(int i = n; i; --i){
	for(int j = i + 1; j <= n; ++j) a[i][n + 1] -= a[i][j] * ans[j];
	ans[i] = a[i][n + 1] / a[i][i];
	}
	return 0;
	}

	bool _v;

	int main(){
	cerr << abs(&_u - &_v) / 1048576.0 << " MB\n";

	n = read();
	for(int i = 1; i <= n; ++i) for(int j = 1; j <= n + 1; ++j) scanf("%lf", &a[i][j]);
	int flag = solve(n);
	if(flag != 0) printf("No Solution\n");
	else for(int i = 1; i <= n; ++i) printf("%.2lf\n", ans[i]);
	return 0;
	}

1.【最大公约数（GCD）和最小公倍数（LCM）】

【基本性质、定理】

【推导结论】

证明

2.费马小定理

3.【裴蜀（Bézout）定理】

扩展欧几里得算法

1.1 解的存在性

1.2 算法介绍

【推导结论】

4.逆元

4.1 费马小定理求逆元

4.2 扩展欧几里得求逆元

4.3 线性求逆元

5.欧拉函数

5.1 定义与性质

线性筛欧拉函数

5.2 欧拉定理

6.离散对数问题

6.1 大步小步算法

6.2 扩展大步小步算法

7.线性同余方程组

7.1 中国剩余定理

7.2 扩展中国剩余定理

8.高斯消元法

8.1过程

模板 P3389 【模板】高斯消元法

高斯消元

高斯约旦消元

8.2 比较

8.3 应用

8.3.1 解异或方程组

公告

常用链接

随笔档案