内部排序总结之----选择类排序（选择、堆）

一、直接选择排序

　　选择排序的思想和冒泡差不多，就是先选出数列中最小或最大的，再选择第二的，不断进行，直到排序完成。它和冒泡不同的是，冒泡排序是交换类排序，是把一个数列假象成两个数列：一个待排序，一个已排序，并且通过不断地把待排序中第一个数插入到已排序数列中合适位置。但是选择类是在每一趟循环中找到最大或者最小的数的下标，再一趟循环结束时交换第一个数据和那个下标的数据。

　　假设需要排序的数列为：

　　2 4 1 6 5 0 7 第一趟循环找到最大值为7；

　　7 4 1 6 5 0 2

 

 

 

　　...

　　7 6 5 4 2 1 0 不断的选出待排序数列中的最大数放到已排序数列的队尾，最终完成排序。

 

void selectSort(int arr[],int len)
{
    int i,j,index,tmp;

    for(i =  0; i < len; i++)
    {
                index = i;

        for(j = i+1; j < len; j++)
        {
            if(arr[j] < arr[tmp])
                index = j;
        }

                tmp = arr[index];
                arr[index] = arr[i];
                arr[i] = tmp;
    }
}

 

直接选择排序总结：

时间复杂度：平均情况O(n²)，最好情况O(n²)，最坏情况O(n²)

空间复杂度：O(1)

稳定性：不稳定

 

二、堆排序

　　堆排序就是利用“堆”这种数据结构的特点进行排序，该排序是速度仅次于快排的一种排序，而且在很多时候，我们会选择堆排序而不是快排，是因为快排的最坏情况时间复杂度为O(n²)（快排是越有序越慢，越无序越快）。为了避免这样我们需要对其进行复杂的优化。所以，堆排序成了我们很好的选择，了解堆排序，就得先了解“堆”的性质。

　　堆：

　　堆实际上是一棵完全二叉树，其任何一非叶节点满足性质：

　　Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]

　　即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。

　　堆分为大根堆和小根堆，满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大根堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小根堆。

　　由上述性质可知大根堆的堆节点的关键字肯定是所有关键字中最大的，小根堆的根节点的关键字是所有关键字中最小的。

---

 

堆排序的思想：

   利用大根堆(小根堆)根节点记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大数据(最小数据)变得简单。

    其基本思想为(大根堆)：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大根堆，此堆为初始的无序区；

    2)将根节点元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

   

操作过程如下：

     1)初始化堆：将R[1..n]构造为堆；

     2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

    因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

 

下面举例说明：

     给定一个整形数组a[]={4,2,1,6,5,3}，对其进行堆排序。

    首先根据该数组元素构建一个完全二叉树，得到

 

　　然后需要构造初始堆，则从最后一个非叶节点开始调整，调整的思路就是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换，调整过程如下：

 

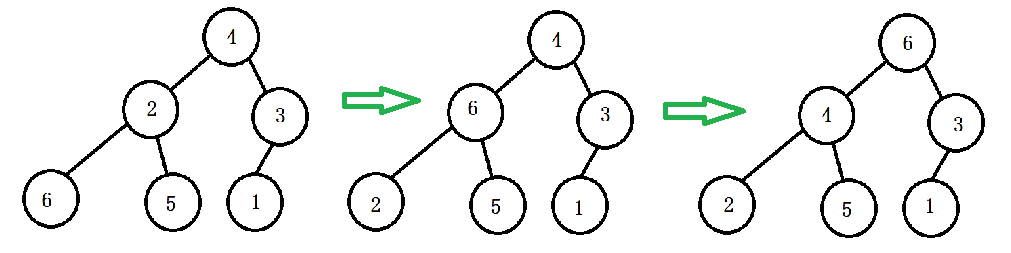
6和4交换后导致4不满足堆的性质，因此需重新调整:

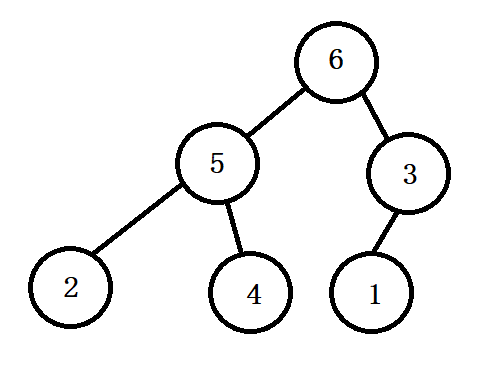
　　这样就得到了初始堆。

---

 

　　开始排序：

　　先把根节点和最后一个节点交换，这样整个数列最大的值就到了最后。

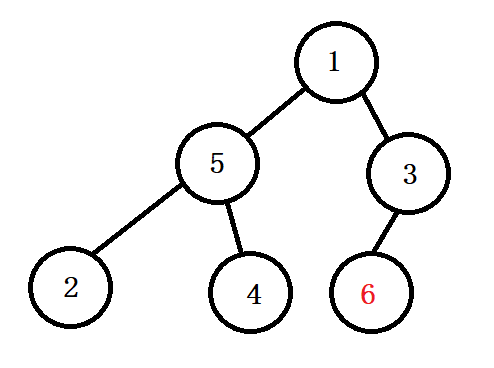
　　但是此时1不满足堆的性质，所以继续调整，此时不再把6纳入调整范围，因为它已经属于已排序数列。

 

　　形成堆之后又可以排序了，把5和1交换。

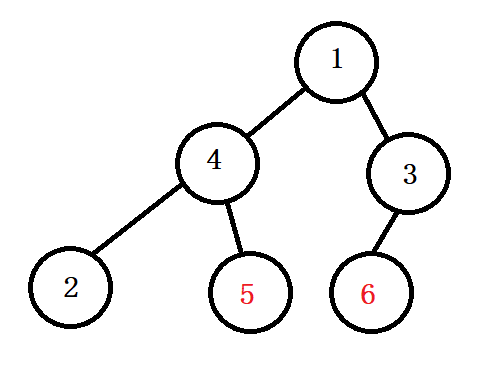
　　继续调整。。。

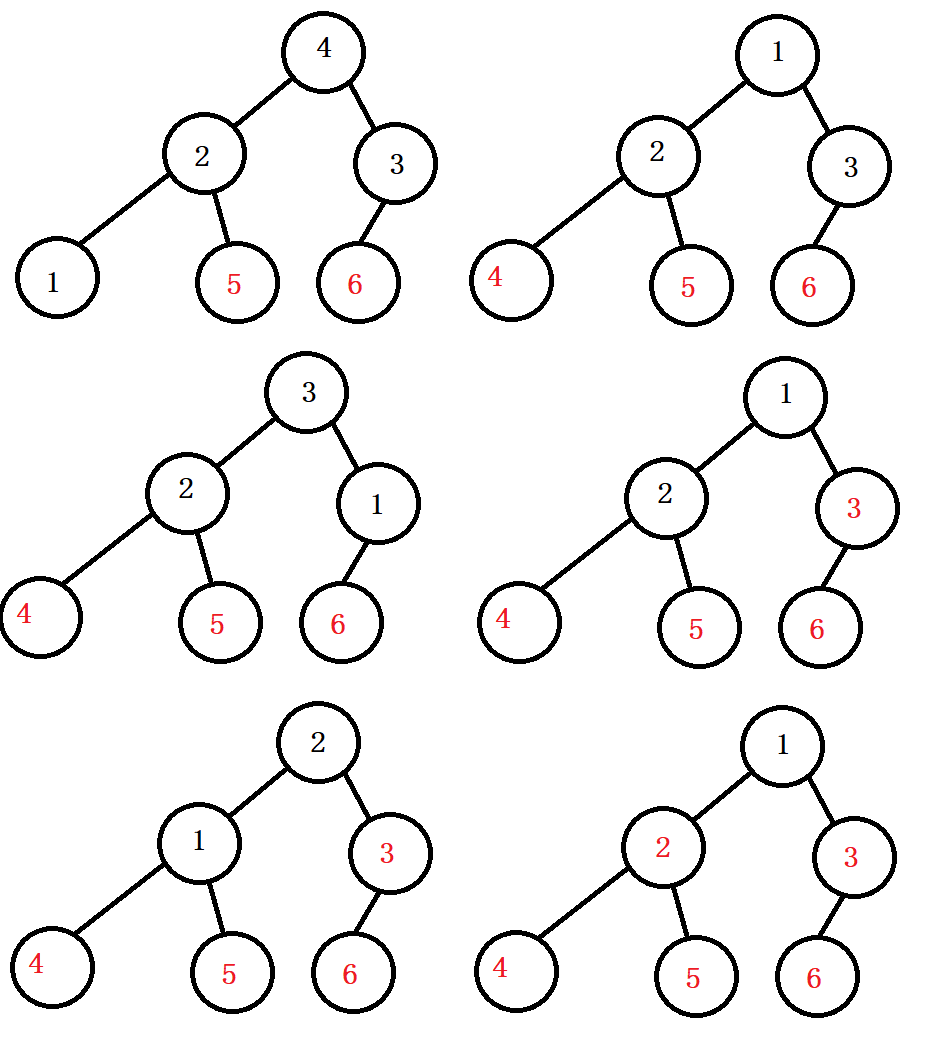
　　（阅读为先→再↓）

　　显然我们可以看到，我们也是遵循每次选出一个最大值或者最小值，同样也是选择排序，只不过直接选择排序中，为了从n个数中选择最大记录，需比较n-1次，然后从n-1个数中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。

void heapAdjust(int arr[],int i,int len) //调整堆 
{
    int min = arr[i];
    for(int j = 2*i; j <= len; j= 2*i)//j为i的左孩子节点，j+1为i的右孩子节点
    {
        if(j < len && arr[j] > arr[j+1])
        {
            j++;
        }
        if(min < arr[j])break;
        arr[i] = arr[j];
        arr[j] = min;
        i = j;
    }
}

void heapSort(int arr[],int len) //堆排序
{
    int i;
    for(i = len/2; i > 0; i--)
    {
        heapAdjust(arr,i,len - 1);
    }
    for(int j = len - 1; j > 0 ; j--)
    {
                int tmp = arr[j];
                arr[j] = arr[1];
                arr[i] = tmp; 
        heapAdjust(arr,1,j-1);
    }

}

 

堆排序排序总结：

时间复杂度：平均情况O(nlog₂n)，最好情况O(nlog₂n)，最坏情况O(nlog₂n)

空间复杂度：O(1)

稳定性：不稳定