ESF、Z-projection和M2DP论文阅读
ESF
Title标题
【2011 ICRB】ESF：Ensemble of Shape Functions for 3D Object Classification. 【code】
简介
引入了一种新的形状描述符 ESF (Ensemble of shape Functions)，这是一种基于描述部分点云表面距离、角度和面积分布的三种不同形状函数的全局形状描述符。
ESF 方法在定义描述符时仅使用形状属性（距离、角度和面积），避免了常规计算。ESF 使用体素网格逼近真实表面，迭代采样 3 个点并计算形状属性。
代表图
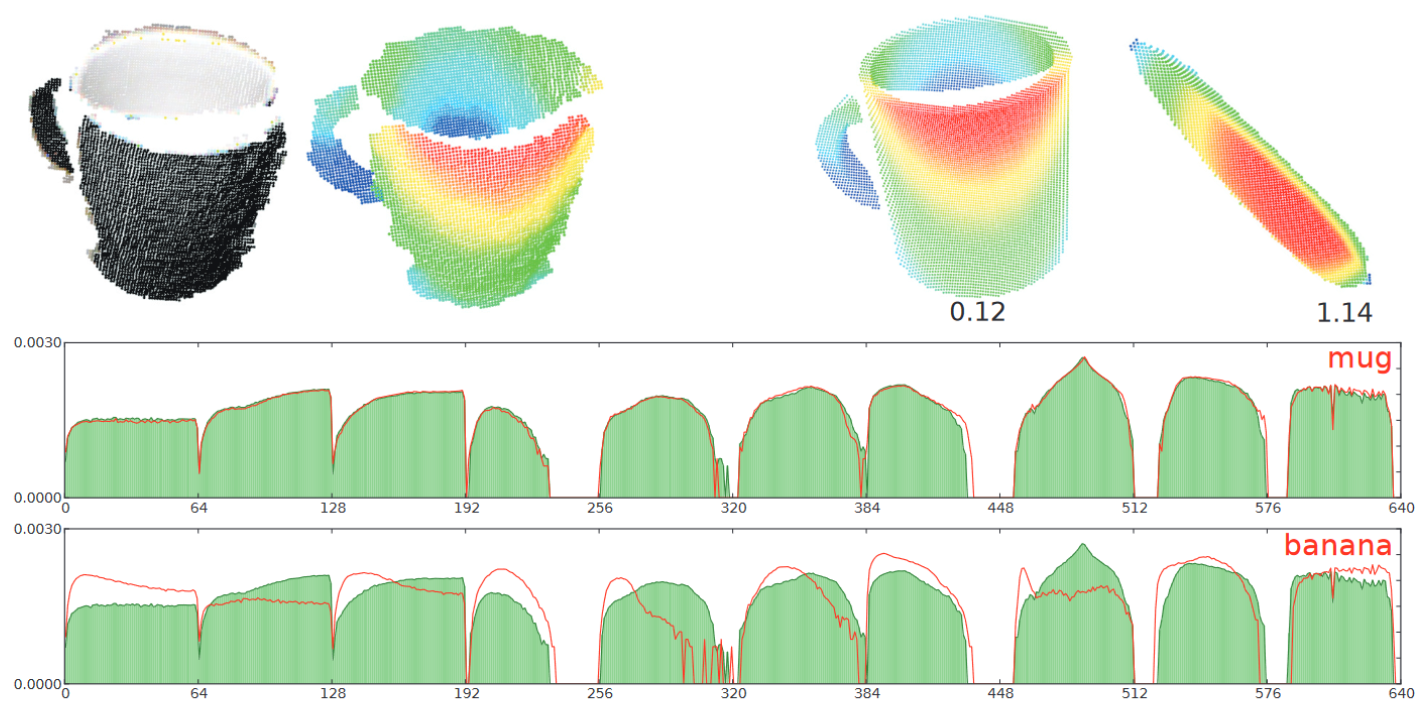
黑色杯子为查询对象，被描绘成左边的图像和它旁边的点云。这里有两个样本数据库对象，一个杯子和一个香蕉。绿色直方图表示查询对象，叠加的红色曲线表示两个数据库对象。查询对象与杯子的相似度是清晰可见的，因为它们的直方图紧密重叠到一个高百分比。香蕉视图生成了完全不同的形状分布直方图，导致了高的不相似度得分。为了更好地观察直方图的形状差异，将直方图绘制在对数尺度上。
结论及创新点
ESF 描述符是 10 个 64 位（10*64=640）大小的形状函数直方图的集合，描述点云簇的特征特性。
ESF 是一种描述点云全局特征的描述符。由 3 种不同形状的函数组合而成，用于描述点云的距离、角度和面积等属性。该算法具有很强的独特性，不需要其他普通信息。同时，它对噪声和不完整的表面很稳健，因此不需要进行预处理等操作。
该算法使用体素网格作为真实表面的近似，然后进行迭代遍历点云中的所有点。对于每次迭代，随机选择３个点，计算点角度（A3）、点面积（D3）、点距离（D2）和点距比（D2Ratio）4 个函数。
- 角度A3：测量三维模型表面上三个随机点之间的夹角。
- 距离D1：测量固定点与随机点之间的距离，固定点一般采用模型边界的质心点。
- 距离D2：测量表面上任意两点之间的距离。
- 面积D3：测量表面上三个随机点之间三角形面积的平方根。
- 体积D4：测量表面上任意四个点之间的四面体体积的立方根。
- 点距比（D2Ratio）：将位于自由空间和物体表面的线条的比例放入一个单独的形状直方图中。
这些形状函数具有简单性和不变性，易于计算并产生对刚性运动不变的分布。
其中对于D2、D3和A3函数，每次迭代除了计算相应的距离、面积和角度之外，还需要检测点对的连线是完全处于表面内（IN）、 完全处于表面外（OUT）还是两者都有（MIXED）， 最后根据检测结果，将计算的函数值分到 3 类直方图 IN、 OUT 或 MIXED 中的 一 个。通 常 情 况 下，ESF 迭代次数是 2000 次。
上图中香蕉的样本 ESF 直方图，分别表示三个角度、三个面积、三个距离和一个距离比形状函数的组合直方图。
Z-projection（Small-Sized Signatures）
Title标题
【2011 SSRR】Loop closure detection using small-sized signatures from 3D LIDAR data.
简介
SmallSize Signatures是一种专门针对激光雷达数据闭环检测问题的简单方法。它首先计算所有点的法线，然后将沿法线 z 轴的分量二值化为直方图作为描述符。
缺点
需要一个预处理步骤来计算所有点的法线。
M2DP
Title标题
【2016 IROS】M2DP: A Novel 3D Point Cloud Descriptor and Its Application in Loop Closure Detection. 【matlab】【python】【C++】
简介
M2DP（multiview 2D projection）方法是2016年发表的，这是一个适用于激光雷达的回环检测法。这是一个比较经典的全局描述符的提取方式，文章发表的时候效果显著，远超许多传统方法。后续回环检测算法论文都会提到该文章。已经成为了回环检测方法 Benchmarking 的标配。该方法首先把三维点云投影到一系列的二维平面上，代表点云不同的视角；然后基于点在平面上的空间密度分布特征，获取每个点云的这种密度分布，或者称为签名（signature）；然后使用这些签名的第一个左右奇异值向量作为描述符。
代表图
结论及创新点
首先对点云进行预处理。回环检测中，描述符需要对三维空间保持平移不变性和旋转不变性。为了保证平移不变性，我们首先使用输入点云的质心作为描述子参考帧的原点。使用主成分分析（PCA）对齐输入点云来实现旋转不变性。对点云进行主成分分析，利用第一和第二个主成分来定义描述子参考坐标系的 x 轴和 y 轴。该步骤假设每一个点云有两个主导方向，这使得我们可以沿着这些主导方向来粗略的将匹配的两个点云对齐。
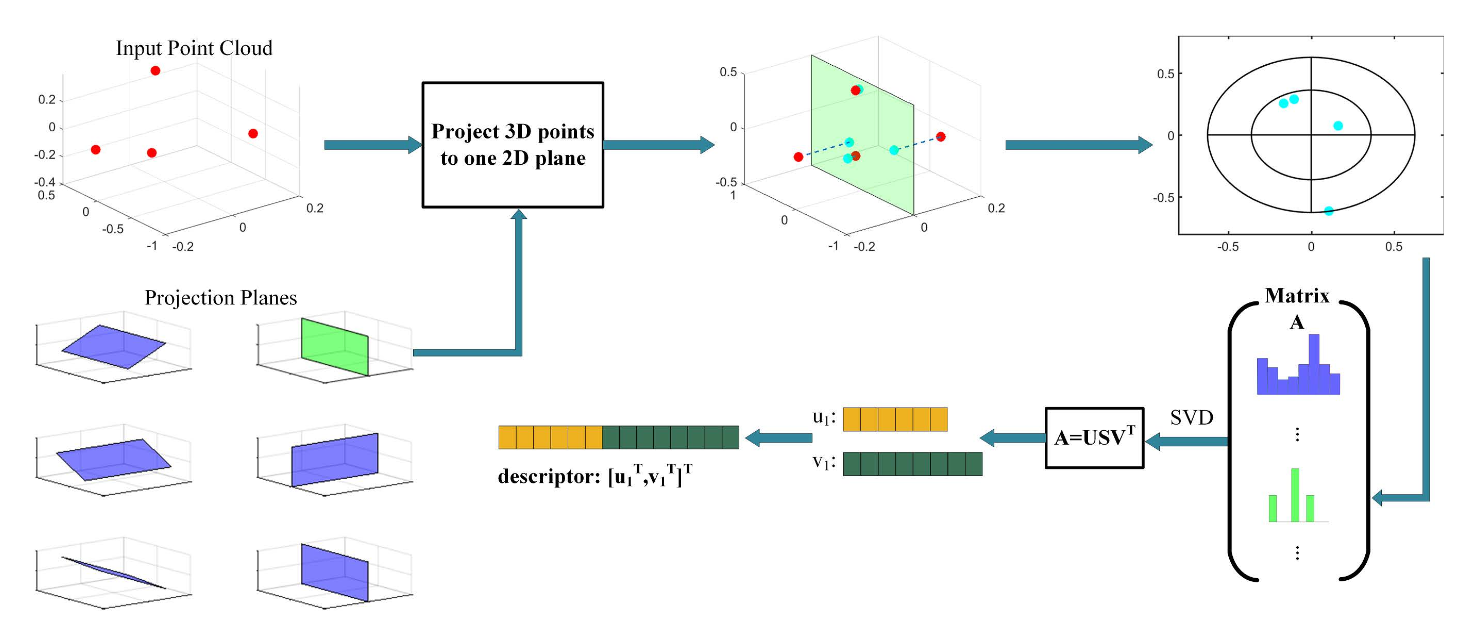
该方法首先把三维点云投影到一系列的二维平面上，代表点云不同的视角（考虑一个三维点云 \(P\) 和两个投影的二维平面 \(X\) 和 \(Y\) ，将 \(P\) 投影到 \(X\) 和 \(Y\) 上的点分别记为 \(P_x\) 和 \(P_y\) 。在假设 \(X\) 和 \(Y\) 不平行且投影不发生遮挡的情况下，我们能够从 \(P_x\) 和 \(P_y\) 以及 \(X\) 和 \(Y\) 之间的角度重建 \(P\) ）。
通过法向量 \(m\) 来定义二维投影平面 \(X\) ，且 \(X\) 需要过原点；另外，法向量可以通过方位角 \(\theta\) 和俯仰角 \(\phi\) 来确定，因此，平面 \(X\) 可由参数对 \([\theta, \phi]\) 唯一确定。把中心原点、 \(x\) 轴、点云投影到平面 \(X\) 上。将二维平面划分为多个容器（bin）。以投影后的中心点为中心，生成 \(l\) 个同心圆，半径为 \([r, 2^2r, …, l^2r]\)，另外，最大半径与最远点到中心点的距离相等。对于上面的一系列圆环，每个圆环都分成 \(t\) 个 bin ，并按照 \(x\) 轴把这些 bin 编号；这样就把一个平面分成了 \(l \times t\) 个bin 。对于每一个 bin ，简单计算其中的点的数量，然后就获得一个 \(lt \times 1\) 的签名向量 \(v_x\) ，以此描述三维点云在平面 \(X\) 上的投影。
然后获得 \(P_x\) 的签名 \(v_x\) 以及 \(P_y\) 的签名 \(v_y\) ，组成签名矩阵 \(A=[v_x^T \quad v_y^T]^T\) 来代表 \(P\) 。
对于每一个点云，计算并比较它的签名矩阵(特征矩阵)来找到它的最近邻居作为匹配候选。设置一个距离阈值，如果两者之间距离小于阈值，则认为是闭环。为避免相邻帧匹配，把当前帧的前后 50 帧排除在外。
可以通过增加投影平面的数量，来获得一个扩增的签名矩阵 \(A\) 。通过使用 \(p\) 个不同的方位角 \(\theta\) 和 \(q\) 个不同的俯仰角 \(\phi\) ，生成 \(pq\) 个不同的二维平面；方位角的步幅为 \(\frac{π}{p}\) ，俯仰角的步幅为 \(\frac{π}{2q}\) 。对于每一个二维平面，都生成一个 \(lt \times 1\) 的二维签名，因此可以得到一个 \(pq \times lt\) 的矩阵 \(A\) 来表示点云，每一行代表一个二维签名。
为了降维压缩签名，在矩阵 \(A\) 上进行奇异值分解 SVD ，将分解后的左、右奇异值矩阵的第一个向量结合起来，作为最终的描述符。
实验部分
本文将提出的 M2DP 算法和现存五种算法进行实验比较：全局描述符 VFH、ESF、Z-projection；局部描述符 SHOT、Spin Image；另外还对比了基于视觉的基准描述符 GIST；
本文使用的数据集为 KITTI 的 00，05，06，07 序列和 Freiburg Campus、Ford Campus；点云数目分别为 4541、2761、1101、1101、77、3817；
本文设计三个实验进行比较：实验一使用原始点云作为输入；实验二采用不同下采样网格大小处理后的点云作为输入，以此测试算法鲁棒性；实验三对每一个点的位置添加一个服从均匀分布的噪声来测试算法对于噪声的鲁棒性；
优点
该方法避免了表面法向量的计算，计算高效，描述准确。
缺点
计算一帧点云的时间需要 300ms， 而一个 10hz 的激光雷达采集数据的时间间隔为 100ms。计算一帧点云描述符的时间远远超过数据采集间隔，它根本无法应用到 SLAM 框架内（有学者曾尝试将它加入到 LIO-SAM 中，但效果不好）。该文章没有明确的提出计算描述符相似度的方式，由于比较相似度的方法很多，不知道具体的方法则无法完全复现论文。
M2DP 无法检测到反向闭环。
参考资料
SLAM回环检测方法总结：https://zhuanlan.zhihu.com/p/593279957
论文解读《M2DP: A Novel 3D Point Cloud Descriptor and Its Application in Loop Closure Detection》：https://blog.csdn.net/weixin_41398920/article/details/111661861
