牛客算法周周练4 - [SDOI2016]齿轮（建图DFS、带权并查集）

牛客算法周周练4 - [SDOI2016]齿轮（建图DFS、带权并查集）

链接：https://ac.nowcoder.com/acm/contest/5505/A
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

现有一个传动系统，包含了N个组合齿轮和M个链条。每一个链条连接了两个组合齿轮u和v，并提供了一个传动比x  : y。
即如果只考虑这两个组合齿轮，编号为u的齿轮转动x圈，编号为v的齿轮会转动y圈。传动比为正表示若编号为u的齿轮顺时针转动，则编号为v的齿轮也顺时针转动。传动比为负表示若编号为u的齿轮顺时针转动，则编号为v 的齿轮会逆时针转动。若不同链条的传动比不相容，则有些齿轮无法转动。我们希望知道，系统中的这Ｎ个组合齿轮能否同时转动。

输入描述:

有多组数据，第一行给定整数Ｔ，表示总的数据组数，之后依次给出Ｔ组数据。
每一组数据的第一行给定整数Ｎ和Ｍ，表示齿轮总数和链条总数。
之后有Ｍ行，依次描述了每一个链条，其中每一行给定四个整数u，v，x和y，表示只考虑这一组联动关系的情况下，编号为u的齿轮转动x圈，编号为v的齿轮会转动y圈。
请注意，x为正整数，而y为非零整数，但是y有可能为负数。
T ≤ 32，N ≤ 1000，M ≤ 10000且x与y的绝对值均不超过100

输出描述:

输出T行，对应每一组数据。首先应该输出标识这是第几组数据，参见样例输出。之后输出判定结果，如果N个组合齿轮可以同时正常运行，则输出Yes，否则输出No。

示例1

输入

2
3 3
1 2 3 5
2 3 5 -7
1 3 3 -7
3 3
1 2 3 5
2 3 5 -7
1 3 3 7

输出

Case #1: Yes
Case #2: No

 

解法一（建图DFS）：

根据题意，建立一个无向图，每条边多记录一个x和y。

我们令起始点u的w值为1.0，然后根据x和y去求下一个点v的w值，中途判断是否矛盾即可。

遍历所有节点，没访问过的w初始化为1.0，然后DFS，如果再次DFS到这个点v，判断w[v]是否等于w[u]*(x/y)，不等直接No就行了。

注意这个图可能不连通

 

具体的看代码吧：

 1 #include <bits/stdc++.h>
 2 typedef long long LL;
 3 #define pb push_back
 4 const int INF = 0x3f3f3f3f;
 5 const double eps = 1e-8;
 6 const int mod = 1e9+7;
 7 const int maxn = 1e5+10;
 8 using namespace std;
 9 
10 struct edge
11 {
12     int to;
13     int x, y;
14     int next;
15 }E[maxn];//注意边的条数
16 int head[maxn], tot;
17 void add(int u,int v,int x,int y)
18 {
19     E[tot].to=v;
20     E[tot].x=x; E[tot].y=y;
21     E[tot].next=head[u];
22     head[u]=tot++;
23 }
24 
25 int n,m;
26 int ok;
27 int vis[maxn];
28 double w[maxn];
29 void init()
30 {
31     tot = 0;
32     ok = 1;
33     memset(head,-1,sizeof(head));
34     memset(vis,0,sizeof(vis));
35 }
36 void DFS(int u, int fa)
37 {
38     for(int i=head[u];i!=-1;i=E[i].next)
39     {
40         int v=E[i].to, x=E[i].x, y=E[i].y;
41         if(v==fa) continue;
42         if(vis[v])
43         {
44             if(fabs(w[v] - w[u]*(1.0*x/y))>eps)//出现矛盾
45             {
46                 ok=0;
47                 return ;
48             }
49         }
50         else
51         {
52             vis[v]=1; w[v]=w[u]*(1.0*x/y);
53             DFS(v, u);
54         }    
55     }
56 }
57 
58 int main()
59 {
60     #ifdef DEBUG
61     freopen("sample.txt","r",stdin); //freopen("data.out", "w", stdout);
62     #endif
63     
64     int T;
65     scanf("%d",&T);
66     for(int k=1;k<=T;k++)
67     {
68         printf("Case #%d: ",k);
69         scanf("%d %d",&n,&m);
70         init();
71         for(int i=1;i<=m;i++)
72         {
73             int u,v,x,y;
74             scanf("%d %d %d %d",&u,&v,&x,&y);
75             add(u,v,x,y);
76             add(v,u,y,x);
77         }
78         for(int i=1;i<=n&&ok;i++)
79         {
80             if(!vis[i])
81             {
82                 vis[i]=1; w[i]=1.0;
83                 DFS(i,-1);
84             }
85         }
86         printf(ok? "Yes\n":"No\n");
87     }
88     
89     return 0;
90 }

 

 

解法二（带权并查集）：

from：Inf_Voltage

根据题意，我们发现如果图中没有环一定满足题意，如果有环且边权之积为1时满足条件，否则一定不满足

很好理解，我们任意取环上一点使之转动一周，经过环的传动回到自己这里一定还是只转一周

处理点之间的关系，并查集是个不错的选择，本题不仅要处理是否成环，还要求出环上的边权积，带权并查集则能够很好的完成这个任务

对于并查集，我们定义fa[i]表示节点i的祖先, w[i]表示从节点i到fa[i]的传动比之积

对于每个链条(u, v, x, y)，如果(u, v)在一 个联通块中， 显然连了u-v后会成环，我们用K=w[u]/w[v]得到u-v的链上的传动比之积，如果K==x/y则满足条件，否则整个传动装置不合法

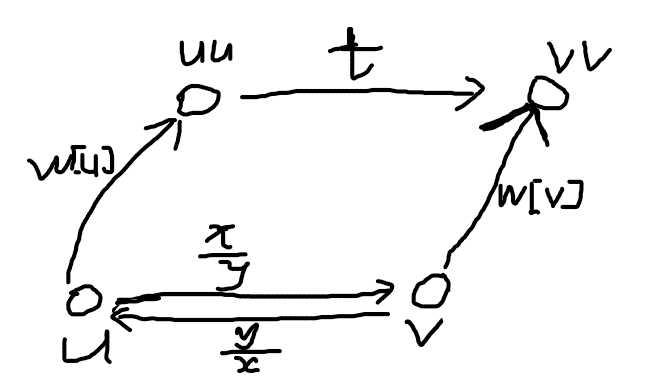
如果(u, v)不在一个联通块中, 我们则需要在fa[u]-fa[v]之间连一 条边权t边，使得t*w[u]/w[v]=x/y 解方程得到t=(x*w[v])/(y*w[u])

 

看看矢量图（公式编出来的）：(y/x)*w[u]*t=w[v]，即t=(x*w[v])/(y*w[u])

 

 

 

需要特别注意的是精度问题，eps=1e-10能过

 

 1 #include <bits/stdc++.h>
 2 typedef long long LL;
 3 #define pb push_back
 4 const int INF = 0x3f3f3f3f;
 5 const double eps = 1e-8;
 6 const int mod = 1e9+7;
 7 const int maxn = 1e5+10;
 8 using namespace std;
 9 
10 int n,m;
11 int ok;
12 double w[maxn];
13 
14 int fa[maxn];
15 void init(int n)
16 {
17     ok = 1;
18     for(int i=1;i<=n;i++)
19         fa[i]=i, w[i]=1.0;
20 }
21 int Find(int x)//带权并查集 
22 {
23     if(x!=fa[x])
24     {
25         int t=fa[x];
26         fa[x]=Find(fa[x]);
27         w[x]*=w[t];
28     }
29     return fa[x];
30 }
31 
32 int main()
33 {
34     #ifdef DEBUG
35     freopen("sample.txt","r",stdin); //freopen("data.out", "w", stdout);
36     #endif
37     
38     int T;
39     scanf("%d",&T);
40     for(int k=1;k<=T;k++)
41     {
42         printf("Case #%d: ",k);
43         scanf("%d %d",&n,&m);
44         init(n);
45         for(int i=1;i<=m;i++)
46         {
47             int u,v,x,y;
48             scanf("%d %d %d %d",&u,&v,&x,&y);
49             if(ok==0) continue;
50             int uu=Find(u), vv=Find(v);
51             if(uu!=vv)
52             {
53                 fa[uu]=vv;
54                 w[uu]*=x*w[v]/(y*w[u]);
55             }
56             else
57             {
58                 if(fabs(w[u]/w[v]-x*1.0/y)>eps) ok=0;
59             }
60         }
61         printf(ok? "Yes\n":"No\n");
62     }
63     
64     return 0;
65 }

 

 

-

posted @ 2020-05-03 02:18  jiamian22  阅读(324)  评论(0)  编辑  收藏  举报