天梯 - 神坛（计算几何、极角排序求三角形最小面积）

天梯 - 神坛（计算几何、极角排序求三角形最小面积）

在古老的迈瑞城，巍然屹立着 n 块神石。长老们商议，选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比，因此神坛的面积越小越好。

特殊地，如果有两块神石坐标相同，或者三块神石共线，神坛的面积为 0.000。

长老们发现这个问题没有那么简单，于是委托你编程解决这个难题。

输入格式：

输入在第一行给出一个正整数 n（3 ≤ n ≤ 5000）。随后 n 行，每行有两个整数，分别表示神石的横坐标、纵坐标（−109 =< 横坐标、纵坐标 < 109）。

输出格式：

在一行中输出神坛的最小面积，四舍五入保留 3 位小数。

输入样例：

8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2

输出样例：

0.500

样例解释

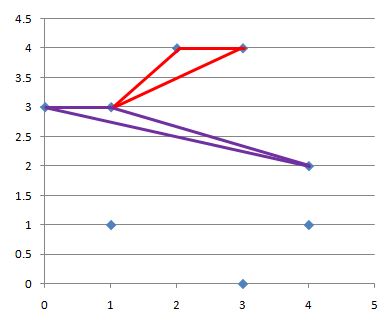
输出的数值等于图中红色或紫色框线的三角形的面积。

altar.JPG

 

题意

N个点求最小三角形。

题解

关于极角排序：https://www.cnblogs.com/aiguona/p/7248311.html

极角排序大致用法：

关于叉积：叉积=0是指两向量平行（重合）；叉积>0，则向量a在向量b的顺时针方向（粗略的理解为在a在b的下方）；叉积<0，则向量a在向量b的逆时针方向（粗略的理解为在a在b的上方）

我们利用叉积按极角从小到大排序。因此可以给定平面上的一些点，把它们按照一个选定的中心点排成顺（逆）时针。

 

先遍历每个点，将其当做中心点，和其他点组成最多n-1个向量，然后按照极角排序的思想将这些向量按顺时针或逆时针排序，然后用叉乘法用相邻两个向量求面积，更新最小值即可。

 

 1 #include <bits/stdc++.h>
 2 const int INF=0x3f3f3f3f;
 3 typedef long long LL;
 4 const double eps =1e-8;
 5 const int mod=1e9+7;
 6 const int maxn=1e5+10;
 7 using namespace std;
 8 
 9 struct node
10 {
11     LL x,y;
12 }P[5005],C[5005];//P存点，C存向量 
13 
14 bool cmp(node a,node b)//向量按顺时针排序
15 {
16     return a.x*b.y-a.y*b.x > 0;
17 }
18 
19 int main()
20 {
21     #ifdef DEBUG
22     freopen("sample.txt","r",stdin);
23     #endif
24     
25     int n;
26     scanf("%d",&n);
27     for(int i=1;i<=n;i++)
28         scanf("%lld %lld",&P[i].x,&P[i].y);
29     LL ans=0x3f3f3f3f3f3f3f3f;
30     for(int i=1;i<=n;i++)
31     {
32         int cnt=0;
33         for(int j=1;j<=n;j++)
34         {
35             if(i!=j)
36             {
37                 C[++cnt].x=P[j].x-P[i].x;
38                 C[cnt].y=P[j].y-P[i].y;
39             }
40         }
41         sort(C+1,C+cnt+1,cmp);
42         for(int j=2;j<=cnt;j++)
43             ans=min(ans,abs(C[j].y*C[j-1].x - C[j].x*C[j-1].y));
44     }
45     printf("%.3f\n",ans*1.0/2);
46     
47     return 0;
48 }

 

 

-

posted @ 2020-03-21 01:37  jiamian22  阅读(625)  评论(0)  编辑  收藏  举报