CodeForces 990D Graph And Its Complement（图和补图、构造）

http://codeforces.com/problemset/problem/990/D

 

 

 

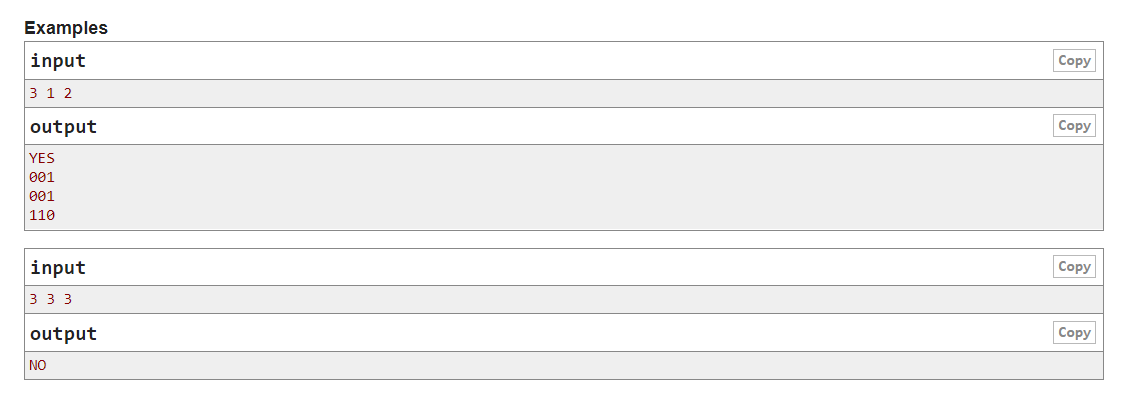
题意：

构造一张n阶简单无向图G，使得其连通分支个数为a，且其补图的连通分支个数为b。

 

题解：

第一眼看到题，一脸懵，嗯？这让我怎么建图？？？

还是菜啊，看别人的题解学习学习吧。。。

参考于：https://www.cnblogs.com/siuginhung/p/9172602.html

这是一个构造问题。

对于一张n阶简单无向图G，若此图不连通，则其补图是连通的。

证明：

首先，在简单无向图G中，若结点u、v（u≠v）不连通，则在其补图中，u、v必然连通。

将图G=<V,E>划分为k个连通分支，Gi=<Vi,Ei>，i=1,2,...,k。在V中任取两点u、v（u≠v）。

若u∈Vi，v∈Vj，且i≠j，则u、v在图G中不连通，则u、v必然在其补图中连通；

若u,v∈Vi，则必然存在w∈Vj，且i≠j，使得u、w和v、w在补图中连通。

于是，在题中，a、b中至少有一个为1。

接下来构造连通分支：若一个n阶简单无向图有k（k≥2）个连通分支，则可以构造其连通分支分别为{1},{2},...,{k-1},{k,k+1,...,n}。

 

代码如下：

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
#define Bug cout<<"---------------------"<<endl
const int mod=1e9+7;
const int maxn=2e5+10;
using namespace std;

int G[1005][1005];

int main()
{
    int n,a,b;
    scanf("%d %d %d",&n,&a,&b);
    if((a!=1&&b!=1)||(n==2||n==3)&&(a==1&&b==1))
        printf("NO\n");
    else
    {
        printf("YES\n");
        if(a==1)
        {
            for(int i=1;i<=n;i++)
            {
                G[i][i]=0;
                for(int j=i+1;j<=n;j++)
                    G[i][j]=G[j][i]=1;
            }
            for(int i=b;i<n;i++)
                G[i][i+1]=G[i+1][i]=0;
        }
        else
        {
            memset(G,0,sizeof(G));
            for(int i=a;i<n;i++)
            {
                G[i][i+1]=G[i+1][i]=1;
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
                printf("%d",G[i][j]);
            printf("\n");
        }
    }
    return 0;
}