线索二叉树
在遍历二叉树的过程中,是按照一定的规则将二叉树中的结点排列成一个线性序列,从而得到二叉树中结点的先序序列或中序序列或后序序列。但是,当以二叉链表作为存储结构时,只能找到结点的左右孩子信息,而不能直接得到结点在任意一个序列中的前驱和后继的信息,而这种信息只有在遍历的动态过程中才能够得到。
为了保存这种信息,就需要使用线索链表。其中指向结点的前驱和后继的指针,叫做线索。添加上线索的二叉树称之为线索二叉树。其结点定义如下:

下面给出按照中序遍历将二叉树中序线索化的算法:

在已经线索化的二叉线索树中,进行中序遍历的算法如下所示:
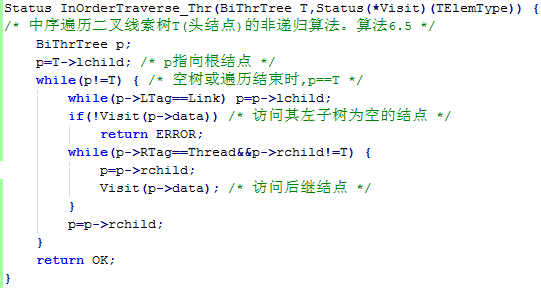
本题中,将会给出一个按照先序遍历得出的字符串,空格代表空的子节点,大写字母代表节点内容。请通过这个字符串建立二叉树,并按照题目描述中算法,中序遍历二叉树并中序线索化二叉树,之后中序遍历输出二叉线索树。
Input
输入只有一行,包含一个字符串S,用来建立二叉树。保证S为合法的二叉树先序遍历字符串,节点内容只有大写字母,且S的长度不超过100。
Output
共一行,包含一串字符,表示按中序遍历二叉线索树得出的节点内容,每个字母后输出一个空格。请注意行尾输出换行。
Sample Input
ABC DE G F
Sample Output
C B E G D F A
HINT
通过线索化二叉树建立二叉线索树,将给普通二叉树添加更快捷的遍历方式。在线索树上进行遍历,只需要先找到序列中的第一个结点,然后依次找结点后继直至其后继为空时而止。而对于中序线索二叉树,由于其固有的性质,在遍历的过程中虽然时间复杂度依旧为O(n),但常数因子将会比普通的算法减小且不需要栈结构辅助,是一种非常优秀的遍历算法。
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 //const double PI=acos(-1); 17 #define Bug cout<<"---------------------"<<endl 18 const int maxn=1e5+10; 19 using namespace std; 20 21 typedef struct BiTNode 22 { 23 char data; 24 BiTNode *lc;//左孩子 25 int ltag;//左标记 26 BiTNode *rc;//右孩子 27 int rtag;//右标记 28 }BiTNode,*BiTree; 29 30 BiTree pre;//辅助指针,指向遍历的上一个结点 31 32 void Create_Tree(BiTree &rt)//先序建树 33 { 34 char c; 35 scanf("%c",&c); 36 if(c==' ') 37 rt=NULL; 38 else 39 { 40 rt=(BiTree)malloc(sizeof(BiTNode)); 41 rt->data=c; 42 rt->ltag=rt->rtag=0; 43 Create_Tree(rt->lc); 44 Create_Tree(rt->rc); 45 } 46 } 47 48 void zhong_vis(BiTree &rt)//中序线索化预处理 49 { 50 if(rt==NULL) 51 return ; 52 zhong_vis(rt->lc); 53 // 54 if(rt->lc==NULL)//没有左孩子 55 { 56 rt->ltag=1;//前驱线索 57 rt->lc=pre;//左孩子指向前驱 58 } 59 if(pre->rc==NULL)//前驱没有右孩子 60 { 61 pre->rtag=1;//后续线索 62 pre->rc=rt;//前驱右孩子指针指向后继 63 } 64 pre=rt;//更新pre,报持pre指向p的前驱 65 // 66 zhong_vis(rt->rc); 67 } 68 69 void ReCreate_Tree(BiTree &Head,BiTree &rt)//加上头结点 70 { 71 Head->ltag=0; 72 Head->rtag=1; 73 Head->rc=Head;//右指针回指 74 if(!rt)//若二叉树为空,则左指针回指 75 Head->lc=Head; 76 else 77 { 78 Head->lc=rt; 79 pre=Head; 80 zhong_vis(rt);//中序遍历进行中序线索化 81 pre->rc=Head;//最后一个结点线索化 82 pre->rtag=1; 83 Head->rc=pre; 84 } 85 } 86 87 void Rezhong_vis(BiTree &hd)//遍历 88 { 89 BiTree p=hd; 90 p=p->lc;//p指向根结点 91 while(p!=hd)//空树或遍历结束 92 { 93 while(p->ltag==0)//循环到中序序列第一个结点 94 p=p->lc; 95 printf("%c ",p->data); 96 while(p->rtag==1&&p->rc!=hd) 97 { 98 p=p->rc; 99 printf("%c ",p->data); 100 } 101 p=p->rc;//p进入其右子树根 102 } 103 } 104 105 int main() 106 { 107 BiTree Head=(BiTree)malloc(sizeof(BiTNode));//头结点 108 BiTree Root=(BiTree)malloc(sizeof(BiTNode));//根结点 109 Create_Tree(Root); 110 ReCreate_Tree(Head,Root); 111 Rezhong_vis(Head); 112 printf("\n"); 113 return 0; 114 }


