前缀和、二维前缀和与差分
先粘上我入门时看的博客:https://blog.csdn.net/qq_41117236/article/details/89438153
声明:以下部分内容摘自该博客,仅供个人复习时用
【引入】
首先给出一个问题:
给定n个数,再给出m个询问,每个询问给出区间Li,Ri和x,要求你在Li到Ri上每一个值都加上x,最后给出一个询问区间L,R的区间和,怎么办?
思考一下:如果暴力,最坏时间复杂度O(n^2);线段树或者树状数组,时间复杂度O(logn);而使用差分可以O(n)。
要使用差分,首先我们来谈谈前缀和。
【前缀和】
什么是前缀和?前缀和是一个数组的某项下标之前(包括此项元素)的所有数组元素的和。
设b[]为前缀和数组,a[]为原数组,根据这句话可以得到前缀和的定义式和递推式:

一维前缀和理解起来比较容易,二维前缀和后边细说,我们先来说说差分。
【差分】
什么是差分?差分是一个数组相邻两元素的差,一般为下标靠后的减去靠前的一个。
设差分数组p[],即:

差分是将数列中的每一项分别与前一项数做差,
例如:
一个序列1 2 5 4 7 3,差分后得到1 1 3 -1 3 -4 -3
这里注意得到的差分序列第一个数和原来的第一个数一样(相当于第一个数减0)
差分序列最后比原序列多一个数(相当于0减最后一个数)
性质:
1、差分序列求前缀和可得原序列
2、将原序列区间[L,R]中的元素全部+1,可以转化操作为差分序列L处+1,R+1处-1
3、按照性质2得到,每次修改原序列一个区间+1,那么每次差分序列修改处增加的和减少的相同
【联系】
前缀和和差分有什么关系呢?
令F(a)表示前缀和数组,G(a)表示差分数组,则 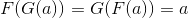
可以说 前缀和 和 差分 是一对互逆过程。
【一维前缀和】
根据上述表达式我们可以以O(1)求出区间[i,j]的区间和 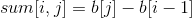
【二维前缀和】
二维前缀和的计算运用了容斥定理,我们来看下图:

显然左上角重合的那一块加了两次,所以我们需要减掉重合的部分。请结合上图理解下列递推式。

【应用+板子】
回到引入中的问题,对于每一个L,R,x,我们只需要在b[L]+x,在b[R]-x,最后做前缀和,O(1)查询即可。
代码如下:
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <math.h> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 const int maxn=1e6+10; 17 using namespace std; 18 int a[1005];//原数组 19 int sum[1005];//前缀和 20 int b[1005];//add标记 21 int main() 22 { 23 int n,m; 24 scanf("%d %d",&n,&m); 25 for(int i=1;i<=n;i++) 26 scanf("%d",&a[i]); 27 while(m--) 28 { 29 int L,R,x; 30 scanf("%d %d %d",&L,&R,&x); 31 //只需对[L,R]区间里的数加p,[R+1,n]这个区间里的数没必要加p。 32 b[L]+=x; 33 b[R+1]-=x; 34 } 35 int add=0;//每一位需要更改的数 36 for(int i=1;i<=n;i++) 37 { 38 add+=b[i];//先计算出该位数要变化的数 39 sum[i]=sum[i-1]+(a[i]+add);//a[i]+add为该位数在操作后最终的数 40 } 41 int l,r; 42 scanf("%d %d",&l,&r); 43 printf("%d\n",sum[r]-sum[l-1]); 44 return 0; 45 }
还是引入中的问题,升级为:
给定一个n*m大小的矩阵a,再给出q个询问,每次询问给定x1,y1,x2,y2和x,表示以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素都加上x,
最后给出一个询问:以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素和,怎么办?
对于每一个x1,y1,x2,y2,我们只需要对数组b
b[x1][y1]+=p; b[x2+1][y2+1]+=p; b[x2+1][y1]-=p; b[x1][y2+1]-=p;
如果(x1,y1)为矩形左下角,(x2,y2)为矩形右下角,竖直向上为x正方向,水平向右为y正方向,那么大致为这样

然后利用上面的公式做二维前缀和即可。
例题:Monitor(二维前缀和+差分)
题解:https://www.cnblogs.com/jiamian/p/11524051.html


