后缀数组

 先粘上我入门时看的博客：

https://www.cnblogs.com/jinkun113/p/4743694.html

https://www.cnblogs.com/victorique/p/8480093.html

https://www.cnblogs.com/jinkun113/p/4743694.html

声明：以下部分内容摘自该博客，仅供个人复习时用

---

 

 

 

后缀数组是让人蒙逼的有力工具！ 后缀数组是处理字符串的有力工具，可以解决很多关于字符串的问题

 

 注意：后缀数组并不是一种算法，而是一种思想。

实现它的方法主要有两种：倍增法O(nlogn) 和 DC3法O(n)

其中倍增法除了仅仅在时间复杂度上不占优势之外，其他的方面例如编程难度，空间复杂度，常数等都秒杀DC3法

建议深入理解倍增法，并能熟练运用（起码8分钟内写出来&&没有错误）。DC3法只做了解。

 

什么是后缀数组

我们先看几条定义：

子串

在字符串s中，取任意i<=j，那么在s中截取从i到j的这一段就叫做s的一个子串

后缀

后缀就是从字符串的某个位置i到字符串末尾的子串，我们定义以s的第i个字符为第一个元素的后缀为suff(i)

后缀数组

把s的每个后缀按照字典序排序，

后缀数组sa[i]就表示排名为i的后缀的起始位置的下标

而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名

简单来说，sa表示排名为i的是啥，rk表示第i个的排名是啥

 

 

基数排序

　　比较的复杂度为O(log n)，如果这个时候再用快速排序的话，依旧需要O(n log^2 n)，虽然已经小多了！但是，这个时候如果使用基数排序，可以进一步优化，达到O(n log n)。

　　首先先来介绍这个以前没听过的排序方法。设存在一序列{73,22,93,43,55,14,28,65,39,81}，首先根据个位数的数值，在遍历数据时将它们各自分配到编号0至9的桶（个位数值与桶号一一对应）中，如下图左侧所示：

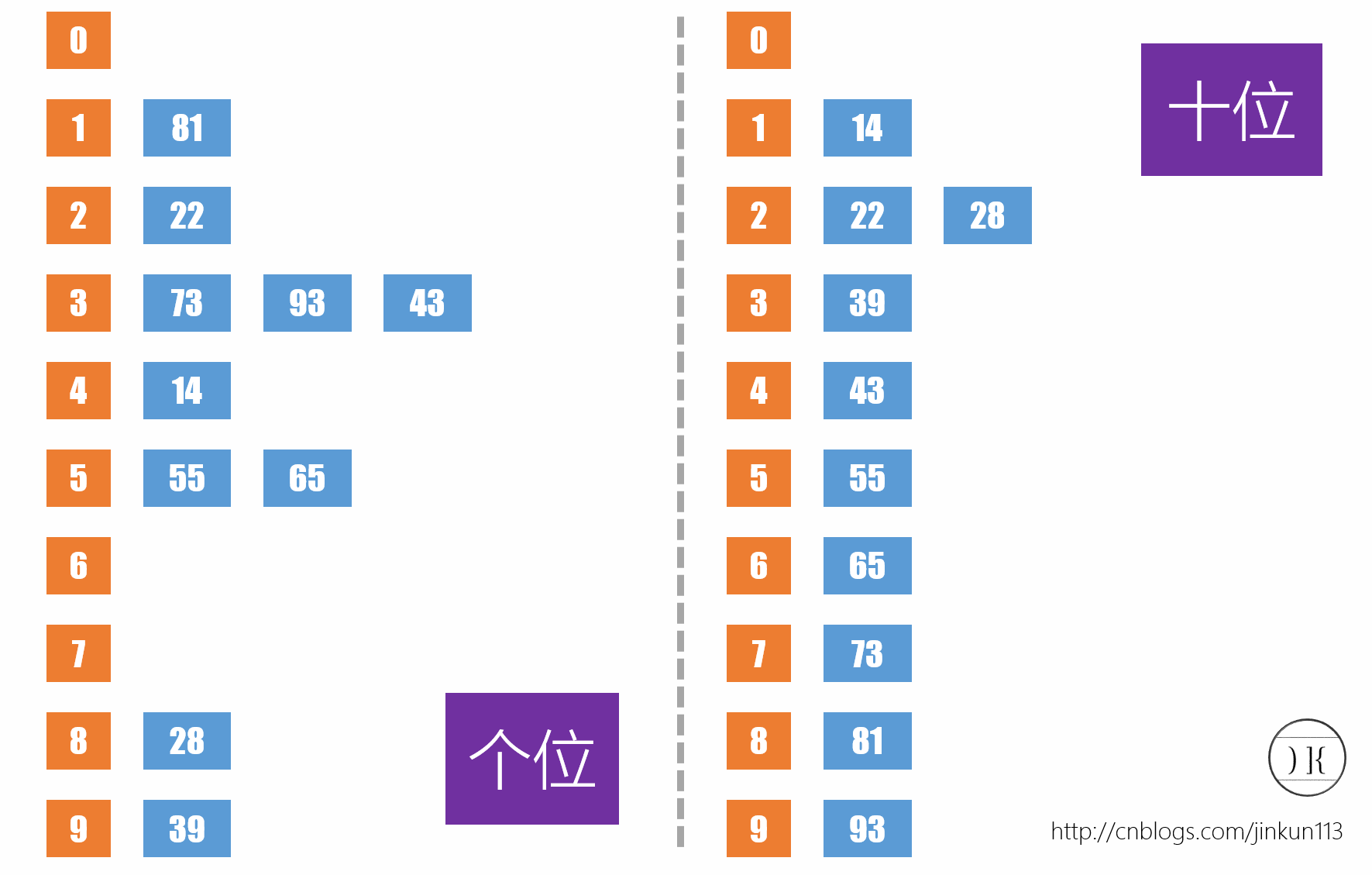
　　得到序列{81,22,73,93,43,14,55,65,28,39}。再根据十位数排序，如右侧，将他们连起来，得到序列{14,22,28,39,43,55,65,73,81,93}。

 

 

 

例题+板子：

https://www.luogu.org/problem/P3809

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <math.h>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
const int maxn=1e6+10;
using namespace std;

char str[maxn];
int sa[maxn];//排名为i的后缀的位置
int rk[maxn];//从第i个位置开始的后缀的排名
int C[maxn];//C数组表示桶，统计每种元素出现了多少次，辅助基数排序 
int X[maxn];//X[i]是第i个元素的第一关键字的字典排名 
int Y[maxn];//Y[i]表示在第二关键字中排名为i的数，其第一关键字的位置

int n,m;
void Get_SA()
{
    for(int i=1;i<=n;i++)
        C[X[i]=str[i]]++;
    for(int i=2;i<=m;i++)//做C的前缀和，我们就可以得出每个关键字最多是在第几名
        C[i]+=C[i-1];
    for(int i=n;i>=1;i--)
        sa[C[X[i]]--] = i;
    
    for(int k = 1; k <= n; k <<= 1)
    {//k:当前倍增的长度，k = x表示已经求出了长度为x的后缀的排名，现在要更新长度为2x的后缀的排名
        int num=0; //num仅仅是一个计数器,示不同的后缀的个数，很显然原字符串的后缀都是不同的，因此num=n时可以退出循环
        
        for(int i=n-k+1;i<=n;i++)//第n-k+1到第n位是没有第二关键字的 所以排名在最前面
            Y[++num]=i;
        for(int i=1;i<=n;i++)
            if(sa[i]>k)
                Y[++num]=sa[i]-k;
//排名为i的数 在数组中是否在第k位以后,即满足(sa[i]>k)，那么它可以作为别人的第二关键字，就把它的第一关键字的位置添加进Y就行了
//所以i枚举的是第二关键字的排名，第二关键字靠前的先入队

        for(int i=1;i<=m;i++)
            C[i]=0;//初始化C桶
        for(int i=1;i<=n;i++)
            C[X[Y[i]]]++;
        //因为上一次循环已经算出了这次的第一关键字 所以直接加就行了
        for(int i=1;i<=m;i++)
            C[i]+=C[i-1];//第一关键字排名为1~i的数有多少个
        for(int i=n;i>=1;i--)
            sa[C[X[Y[i]]]--]=Y[i];
//因为Y的顺序是按照第二关键字的顺序来排的,第二关键字靠后的，在同一个第一关键字桶中排名越靠后

        swap(X,Y);//这里不用想太多，因为要生成新的X时要用到旧的，就把旧的复制下来，没别的意思
        num=1;
        X[sa[1]]=1;
        for(int i=2;i<=n;i++)//因为sa[i]已经排好序了，所以可以按排名枚举，生成下一次的第一关键字X; 
            X[sa[i]]=(Y[sa[i]]==Y[sa[i-1]] && Y[sa[i]+k]==Y[sa[i-1]+k]) ? num : ++num;
        if(num==n)
            break;
        m=num;//这里就不用那个122了，因为都有新的编号了
    }
}

int main()
{
    gets(1+str);
    n=strlen(1+str);
    m=122;
    Get_SA();
    for(int i=1;i<=n;i++)
    {
        if(i==1)
            printf("%d",sa[i]);
        else
            printf(" %d",sa[i]);
    }
    printf("\n");
    return 0;
}

 

于是求出了所有后缀的排序，有什么用呢？主要是用于求它们之间的最长公共前缀（Longest Common Prefix，LCP）

最长公共前缀——后缀数组的辅助工具

什么是LCP？

我们定义LCP(i,j)为suff(sa[i])与suff(sa[j])的最长公共前缀

为什么要求LCP？

后缀数组这个东西，不可能只让你排个序就完事了……大多数情况下我们都需要用到这个辅助工具LCP来做题的

关于LCP的几条性质

显而易见的

1. LCP(i,j)=LCP(j,i);
2. LCP(i,i)=len(sa[i])=n-sa[i]+1;

这两条性质有什么用呢？对于i>j的情况，我们可以把它转化成i<j，对于i==j的情况，我们可以直接算长度，所以我们直接讨论i<j的情况就可以了。

我们每次依次比较字符肯定是不行的，单次复杂度为O(n)，太高了，所以我们要做一定的预处理才行。

LCP Lemma

LCP(i,k)=min(LCP(i,j),LCP(j,k)) 对于任意1<=i<=j<=k<=n

证明：设p=min{LCP(i,j),LCP(j,k)}，则有LCP(i,j)≥p,LCP(j,k)≥p。

设suff(sa[i])=u,suff(sa[j])=v,suff(sa[k])=w;

所以u和v的前p个字符相等，v和w的前p个字符相等

所以u和w的前p的字符相等，LCP(i,k)>=p

设LCP(i,k)=q>p 那么q>=p+1

因为p=min{LCP(i,j),LCP(j,k)}，所以u[p+1]!=v[p+1] 或者 v[p+1]!=w[p+1]

但是u[p+1]=w[p+1] 这不就自相矛盾了吗

所以LCP(i,k)<=p

综上所述LCP(i,k)=p=min{LCP(i,j),LCP(j,k)}

LCP Theorem

LCP(i,k)=min(LCP(j,j-1)) 对于任意1<i<=j<=k<=n

这个结合LCP Lemma就很好理解了

我们可以把i~k拆成两部分i~(i+1)以及(i+1)~k

那么LCP(i,k)=min(LCP(i,i+1),LCP(i+1,k))

我们可以把(i+1)~k再拆，这样就像一个DP，正确性显然

怎么求LCP？

我们设height[i]为LCP(i,i-1) ，1<i<=n，显然height[1]=0;（height[i]表示sa[i-1]和sa[i]的最长公共前缀长度）

由LCP Theorem可得，LCP(i,k)=min(height[j]) i+1<=j<=k

那么height怎么求，枚举吗？NONONO，我们要利用这些后缀之间的联系

设h[i]=height[rk[i]]，同样的，height[i]=h[sa[i]];

那么现在来证明最关键的一条定理：

h[i]>=h[i-1]-1;

证明过程来自曲神学长的blog，我做了一点改动方便初学者理解：

首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串，注意k不一定是i-2，因为第k个字符串是按字典序排名来的i-1前面那个，并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。

这时，依据height[]的定义，第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]]，现在先讨论一下第k+1个字符串和第i个字符串的关系。

第一种情况，第k个字符串和第i-1个字符串的首字符不同，那么第k+1个字符串的排名既可能在i的前面，也可能在i的后面，但没有关系，因为height[rk[i-1]]就是0了呀，那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1，也就是h[i]>=h[i-1]-1。

第二种情况，第k个字符串和第i-1个字符串的首字符相同，那么由于第k+1个字符串就是第k个字符串去掉首字符得到的，第i个字符串也是第i-1个字符串去掉首字符得到的，那么显然第k+1个字符串要排在第i个字符串前面。同时，第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]]，

那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。

到此为止，第二种情况的证明还没有完，我们可以试想一下，对于比第i个字符串的排名更靠前的那些字符串，谁和第i个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第i个字符串的那个字符串了呀，即sa[rank[i]-1]。但是我们前面求得，有一个排在i前面的字符串k+1，LCP(rk[i],rk[k+1])=height[rk[i-1]]-1;

又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1)

所以height[rk[i]]>=height[rk[i-1]]-1，也即h[i]>=h[i-1]-1。

 

 

令LCP(i,j)为第i小的后缀和第j小的后缀（也就是Suffix(SA[i])和Suffix(SA[j])）的最长公共前缀的长度，则有如下两个性质：

1. 对任意i<=k<=j，有LCP(i,j) = min(LCP(i,k),LCP(k,j))
2. LCP(i,j)=min(i<k<=j)(LCP(k-1,k))

第一个性质是显然的，它的意义在于可以用来证明第二个性质。第二个性质的意义在于提供了一个将LCP问题转换为RMQ问题的方法：
令height[i]＝LCP(i-1,i)，即height[i]代表第i小的后缀与第i-1小的后缀的LCP，则求LCP(i,j)就等于求height[i+1]~height[j]之间的RMQ，套用RMQ算法就可以了，复杂度是预处理O(nlogn)，查询O(1)

然后height的求法要用到另一个数组：令h[i]=height[SA[i]]，即h[i]表示Suffix(i)的height值（同时height[i]就表示Suffix(SA[i])的height值），则有height[i]=h[Rank[i]]
然后h[i]有个性质：

• h[i] >= h[i-1]-1

用这个性质我们在计算h[i]的时候进行后缀比较时只需从第h[i-1]位起比较，从而总的比较的复杂度是O(n)，也就是说h数组在O(n)的时间内解决了。h解决了height也解决了，从而整个LCP问题就解决了^_^

然后后缀数组的应用就是利用它的LCP在需要字符串比较时降低复杂度。同时由于后缀数组的有序性可以很方便地使用二分

于是总结一下要点：

• 利用倍增算法在O(nlogn)的时间内对后缀数组进行排序
• 利用h数组的性质在O(n)的时间内求出排序后相邻后缀间的LCP数组height
• 利用LCP的性质将平凡LCP问题转化为height数组上的RMQ问题

 

 

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <math.h>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
const int maxn=1e6+10;
using namespace std;

char str[maxn];
int sa[maxn];//排名为i的后缀的位置
int rk[maxn];//从第i个位置开始的后缀的排名
int C[maxn];//C数组表示桶，统计每种元素出现了多少次，辅助基数排序 
int X[maxn];//X[i]是第i个元素的第一关键字的字典排名 
int Y[maxn];//Y[i]表示在第二关键字中排名为i的数，其第一关键字的位置
int height[maxn];//height[i]表示排名为i和排名为i-1字符串的最长公共前缀长度 

int n,m;
void Get_sa()
{
    for(int i=1;i<=n;i++)
        C[X[i]=str[i]]++;
    for(int i=2;i<=m;i++)//做C的前缀和，我们就可以得出每个关键字最多是在第几名
        C[i]+=C[i-1];
    for(int i=n;i>=1;i--)
        sa[C[X[i]]--] = i;
    
    for(int k = 1; k <= n; k <<= 1)
    {//k:当前倍增的长度，k = x表示已经求出了长度为x的后缀的排名，现在要更新长度为2x的后缀的排名
        int num=0; //num仅仅是一个计数器,示不同的后缀的个数，很显然原字符串的后缀都是不同的，因此num=n时可以退出循环
        
        for(int i=n-k+1;i<=n;i++)//第n-k+1到第n位是没有第二关键字的 所以排名在最前面
            Y[++num]=i;
        for(int i=1;i<=n;i++)
            if(sa[i]>k)
                Y[++num]=sa[i]-k;
//排名为i的数 在数组中是否在第k位以后,即满足(sa[i]>k)，那么它可以作为别人的第二关键字，就把它的第一关键字的位置添加进Y就行了
//所以i枚举的是第二关键字的排名，第二关键字靠前的先入队

        for(int i=1;i<=m;i++)
            C[i]=0;//初始化C桶
        for(int i=1;i<=n;i++)
            C[X[Y[i]]]++;
        //因为上一次循环已经算出了这次的第一关键字 所以直接加就行了
        for(int i=1;i<=m;i++)
            C[i]+=C[i-1];//第一关键字排名为1~i的数有多少个
        for(int i=n;i>=1;i--)
            sa[C[X[Y[i]]]--]=Y[i];
//因为Y的顺序是按照第二关键字的顺序来排的,第二关键字靠后的，在同一个第一关键字桶中排名越靠后

        swap(X,Y);//这里不用想太多，因为要生成新的X时要用到旧的，就把旧的复制下来，没别的意思
        num=1;
        X[sa[1]]=1;
        for(int i=2;i<=n;i++)//因为sa[i]已经排好序了，所以可以按排名枚举，生成下一次的第一关键字X; 
            X[sa[i]]=(Y[sa[i]]==Y[sa[i-1]] && Y[sa[i]+k]==Y[sa[i-1]+k]) ? num : ++num;
        if(num==n)
            break;
        m=num;//这里就不用那个122了，因为都有新的编号了
    }
}

void Get_height()
{
    int k=0;
    for(int i=1;i<=n;i++)//求出rk 
        rk[sa[i]]=i;

    for(int i=1;i<=n;i++)
    {
        if(rk[i]==1)//第一名height为0
            continue;
        if(k)//h[i]>=h[i-1]-1;
            k--;
        int j=sa[rk[i]-1];
        while(j+k<=n&&i+k<=n&&str[i+k]==str[j+k])
            k++;
        height[rk[i]]=k;//h[i]=height[rk[i]];
    }    
}

int main()
{
    gets(1+str);
    n=strlen(1+str);
    m=122;//n表示原字符串长度，m表示字符个数，ASCII('z')=122,我们第一次读入字符直接不用转化，按原来的ASCII码来就可以了
    Get_sa();
    Get_height();
    printf("sa:");
    for(int i=1;i<=n;i++)
    {
        printf("%d",sa[i]);
        if(i==n)
            printf("\n");
    }
    printf("rk:");
    for(int i=1;i<=n;i++)
    {
        printf("%d",rk[i]);
        if(i==n)
            printf("\n");
    }
    printf("height:");
    for(int i=1;i<=n;i++)
    {
        printf("%d",height[i]);
        if(i==n)
            printf("\n");
    }
    return 0;
}

 

 

 

 

 

 

经典应用

两个后缀的最大公共前缀

lcp(x,y)=min(heigh[x−y])， 用rmq维护，O(1)查询

可重叠最长重复子串

Height数组里的最大值

不可重叠最长重复子串 POJ1743

首先二分答案x，对height数组进行分组，保证每一组的minheight都>=x>=x

依次枚举每一组，记录下最大和最小长度，多sa[mx]−sa[mi]>=x那么可以更新答案

本质不同的子串的数量

枚举每一个后缀，第i个后缀对答案的贡献为len−sa[i]+1−height[i]

 

 

4个比较基础的应用
Q1：一个串中两个串的最大公共前缀是多少？
A1：这不就是Height吗？用rmq预处理，再O(1)查询。

Q2：一个串中可重叠的重复最长子串是多长？
A2：就是求任意两个后缀的最长公共前缀，而任意两个后缀的最长公共前缀都是Height 数组里某一段的最小值，那最长的就是Height中的最大值。

Q3：一个串种不可重叠的重复最长子串是多长？
A3：先二分答案，转化成判别式的问题比较好处理。假设当前需要判别长度为k是否符合要求，只需把排序后的后缀分成若干组，其中每组的后缀之间的Height 值都不小于k，再判断其中有没有不重复的后缀，具体就是看最大的SA值和最小的SA值相差超不超过k，有一组超过的话k就是合法答案。

A4：一个字符串不相等的子串的个数是多少？
Q4：每个子串一定是某个后缀的前缀，那么原问题等价于求所有后缀之间的不相同的前缀的个数。而且可以发现每一个后缀Suffix[SA[i]]的贡献是Len - SA[i] + 1,但是有子串算重复，重复的就是Heigh[i]个与前面相同的前缀，那么减去就可以了。最后，一个后缀Suffix[SA[i]]的贡献就是Len - SA[k] + 1 - Height[k]。
对于后缀数组更多的应用这里就不详细阐述，经过思考后每个人都会发现它的一些不同的用途，它的功能也许比你想象中的更强大！

 

 

 

---

 声明：我博客里有大量的从别的博客复制过来的代码，分析，以及理解，但我一律会在文章后面标记原博客大佬博客地址，其中部分会加以连接。 绝无抄袭的意思，只是为了我在复习的时候找博客方便。如有原作者对此有不满，请在博客留言，我一定会删除该博文。