排序算法总结
O(n2)的排序算法

冒泡排序
//冒泡排序
template <typename T>
void bubbleSort(T *arr, int size)
{
for (int i = 0; i < size; ++i)
{
for (int j = 0; j < size - i - 1; ++j)
{
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
}
插入排序
template<typename T>
void insertSort(T *arr,int size)
{
for(int i = 0;i < size;++i)
{
int j;
for(j = i;j > 0 && arr[j] < arr[j-1];--j){swap(arr[j],arr[j-1]);}
}
}
选择排序
//选择排序 复杂度O(n^2)
template<typename T>
void selectionSort(T *arr,int size)
{
int k;
for(int i = 0;i < size-1; ++i)
{
k = i;
for(int j = i+1;j < size;++j)
if(arr[j] < arr[k])
k = j;
if(k != i) mySwap(arr[k],arr[i]);
}
}
测试排序使用时间的时候,总是选择排序快于插入排序,按理说,插入排序应该比选择排序要快啊,因为插入排序可以提前终止循环,这是为什么呢?

原因是选择排序比较的是下标,而插入排序每一次比较都要交换,而交换所耗费的时间是高于简单的比较的。
插入排序优化-将交换变成赋值
template<typename T>
void insertSort(T *arr,int size)
{
for(int i = 0;i < size;++i)
{
T e = arr[i];
int j;
for(j = i;j > 0 && arr[j-1] > e;--j){arr[j] = arr[j-1];}
arr[j] = e;
}
}
运行时间明显变快了
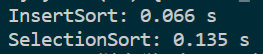
对于近乎有序的数据来说,插入排序的速度要快很多,近乎$O (n)$。而插入排序的实际应用有很多,比如日志,日志的时间是近乎有序的,但是生成日志可能会出错,需要进行时间排序处理,这个时候使用插入排序会更好;还有银行的一些流水单等等
拓展:
C++运算符重载
一般在类中实现,有两种可以实现的方法
运算符重载例子,使用在一个类中
class Student { public: string name; int score; bool operator<(const Student &otherStudent) { return this->score < otherStudent.score; } friend ostream &operator<<(ostream &os, const Student &student) { os << "Student:" << student.name << " "<<student.score<<endl; return os; } };
-
使用友元函数
返回值类型 operator 运算符(形参表) { ... } //例Complex是一个复数类 friend Complex operator+(const Complex &c1,const Complex &c2){ return Complex(c1.i + c2.i,c1.j + c2.j); } -
使用类里面的函数
返回值类型 operator 运算符(形参表) { ... } //例Complex是一个复数类 Complex operator+(const Complex &complex){ return Complex(this->i + complex.i,this->j + complex.j); }
它们的区别就是参数的个数不同以及需不需要加上fridend这个关键字
O(nlog(n))的排序算法
归并排序
代码实现
template <typename T>
void __merge(T *arr, int l, int middle, int r)
{
T aux[r - l + 1];
for (int i = l; i <= r; ++i)
aux[i - l] = arr[i];
int i = l, j = middle + 1;
for (int k = l; k <= r; ++k)
{
if (i > middle)
{
arr[k] = aux[j - l];
j++;
}
else if (j > r)
{
arr[k] = aux[i - l];
i++;
}
else if (aux[i - l] < aux[j - l])
{
arr[k] = aux[i - l];
i++;
}
else
{
arr[k] = aux[j - l];
j++;
}
}
}
template <typename T>
void __mergeSort(T *arr, int l, int r)
{
if (l >= r)
return;
int middle = (l + r) / 2;
__mergeSort(arr, l, middle);
__mergeSort(arr, middle+1, r);
if(arr[middle] > arr[middle+1])
__merge(arr, l, middle, r);
}
//归并排序
template <typename T>
void mergeSort(T *arr, int size)
{
__mergeSort(arr, 0, size - 1);
}
下面这段代码的标记部分需要考虑溢出的问题
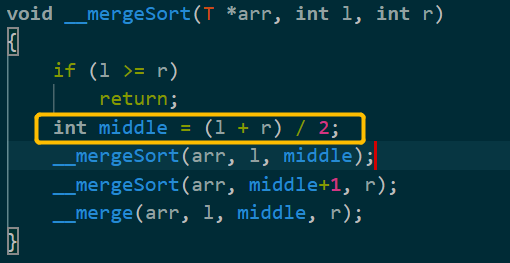
归并排序快是快,但是要耗费多一倍$O(n)$的存储空间,也就是使用空间换时间。
希尔排序
动画演示(来自@五分钟算法):

代码实现:
//希尔排序
template <typename T>
void shellSort(T *arr, int size)
{
int dk[] = {5, 3, 1};
for (int index = 0; index < 3; ++index)
{
for (int i = 0; i < size / dk[index]; ++i)
{
int j;
int e = arr[i];
for (j = i + dk[index]; j > dk[index] && arr[j] > e; j -= dk[index])
{
arr[j] = arr[j - dk[index]];
}
arr[j] = e;
}
}
}
希尔排序相当于是插入排序的升级版,增加了一个步长参数,使用希尔排序可以让零散的数据实现跳跃行的交换,最后逐渐将数组转化为有序,这样最后使用步长为1的插入排序就非常快了。
快速排序
被称为二十世纪影响最大的算法之一!
动画演示(来自@五分钟算法):

代码实现:
template<typename T>
int __partition(T *arr,int l,int r){
T v = arr[l];
int j = l;
for(int i = l+1;i <= r;++i){
if(arr[i] < v){
swap(arr[i],arr[++j]);
}
}
swap(arr[l],arr[j]);
return j;
}
template<typename T>
void __quickSort(T *arr,int l,int r)
{
if(l >= r) return;
int p = __partition(arr,l,r);
__quickSort(arr,l,p-1);
__quickSort(arr,p+1,r);
}
//快速排序
template<typename T>
void quickSort(T *arr,int size)
{
__quickSort(arr,0,size-1);
}
优化一:
在数组的元素个数小于15个的时候使用插入排序进行优化:
template<typename T>
void __quickSort(T *arr,int l,int r)
{
+ if(r - l <= 15) insertionSort(arr,l,r);
int p = __partition(arr,l,r);
__quickSort(arr,l,p-1);
__quickSort(arr,p+1,r);
}
优化二:
使用随机值作为划分标准
template<typename T>
int __partition(T *arr,int l,int r){
+ swap(arr[l],arr[rand() % (r-l+1) + l]);
T v = arr[l];
int j = l;
for(int i = l+1;i <= r;++i){
if(arr[i] < v){
swap(arr[i],arr[++j]);
}
}
swap(arr[l],arr[j]);
return j;
}
template<typename T>
void quickSort(T *arr,int size)
{
+ srand(time(NULL));
__quickSort(arr,0,size-1);
}
缺点:
- 在近乎有序的数组排序中,快速排序的性能很差。时间复杂度也近乎$O(n^2 )$
- 对于有很多重复元素的数组,快速排序的性能也很差
快速排序版本二:两路快排
使用两个下标分别处理大于v与小于v的部分。(v为基准元素)
代码实现:
template<typename T>
int __partition2(T *arr,int l,int r){
swap(arr[l],arr[rand() % (r-l+1) + l]);
T v = arr[l];
int i = l + 1,j = r;
while(true)
{
while(arr[i] < v && i <= r) ++i;
while(arr[j] > v && j >= l+1) --j;
if(i > j) break;
swap(arr[i++],arr[j--]);
}
swap(arr[l],arr[j]);
return j;
}
template<typename T>
void __quickSort2(T *arr,int l,int r)
{
if(r - l<= 15){
insertSort(arr,l,r);
return;
}
int p = __partition2(arr,l,r);
__quickSort2(arr,l,p-1);
__quickSort2(arr,p+1,r);
}
//快速排序版本二,双路快排
template<typename T>
void quickSort2(T *arr,int size)
{
srand(time(NULL));
__quickSort2(arr,0,size-1);
}
快速排序版本三:三路快排
使用三个下标分别处理大于v、等于v与小于v的部分。(v为基准元素)
代码实现:
template<typename T>
void __quickSort3(T *arr,int l,int r)
{
if(r - l<= 15){
insertSort(arr,l,r);
return;
}
swap(arr[l],arr[rand() % (r-l+1) + l]);
T v = arr[l];
int lt = l; //arr[l+1...lt] < v
int gt = r + 1; //arr[gt...r] > v
int i = l+1; //arr[lt+1...i] == v
while(i < gt){
if(arr[i] < v){
swap(arr[i++],arr[++lt]);
}else if(arr[i] > v){
swap(arr[i],arr[--gt]);
}else{
i++;
}
}
swap(arr[l],arr[lt]);
__quickSort3(arr,l,lt-1);
__quickSort3(arr,gt,r);
}
//快速排序版本三,三路快排
template<typename T>
void quickSort3(T *arr,int size)
{
srand(time(NULL));
__quickSort3(arr,0,size-1);
}
堆排序
基数排序
桶排序
排序算法总结
图片:

未完待续......🛴
参考:
作者:Victor Hong
出处:https://www.cnblogs.com/jiahongwu/
Blog:http://vhope.cf/"
本文版权归作者所有;欢迎转载!请注明文章作者和原文连接。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号