有监督分类:决策树以及随机森林
1:决策树
1.1决策树可以分为两个阶段

1.2:熵和Gini系数:

【注】熵和Gini系数的特点(内部越混乱则熵或Gini系数值越大,否则越小)
熵和Gini系数拟解决的问题:熵和Gini系数的引入是为了判断谁作为决策树的根节点?
如何解决:通过信息增益(gain(某一属性/特征)=原始熵值-节点的熵值)的大小来判断熵的降低速度。

1.3决策树的三种算法

c4.5拟解决的问题:存在一些特征(属性)含有多个特征值(属性值),然而每个特征值对应的样本又非常的少,就会使得信息增益很大,但是分类效果并不好?
c4.5解决办法:引入信息增益率=信息增益/节点自身的熵值
评价函数:Nt为叶子节点中样本的个数,H(t)为叶子节点的熵值(即叶子节点内部属性值的熵值和)

【注】节点的熵值和节点自身的熵值的区别:节点的熵值表示,节点内的属性值的熵值和;节点自身的熵值表示,节点本身在所在同一层节点的熵值和。
1.4预剪枝和后剪枝
拟解决问题:当决策树过于庞大时,证明决策树的分支过多以及高度过高,就会导致出现过拟合的现象,从而导致在测试集中取得的效果并不好?
解决办法如图:
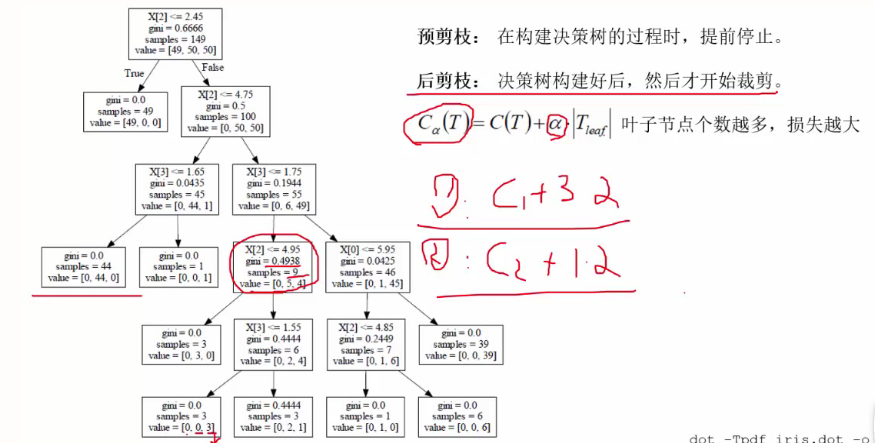
预剪枝的方法例如:设置树的深度;设置节点内的样本数量等。
后剪枝的方法:通过比较某一个节点不分裂(计算时|Tleaf|=1,即自身为叶子节点)与分裂的Ca(T)的大小,如果不分裂的损失值较小,则将其分支剪掉。
1.5参数详解


2:随机森林
2.1随机森林的工作原理:
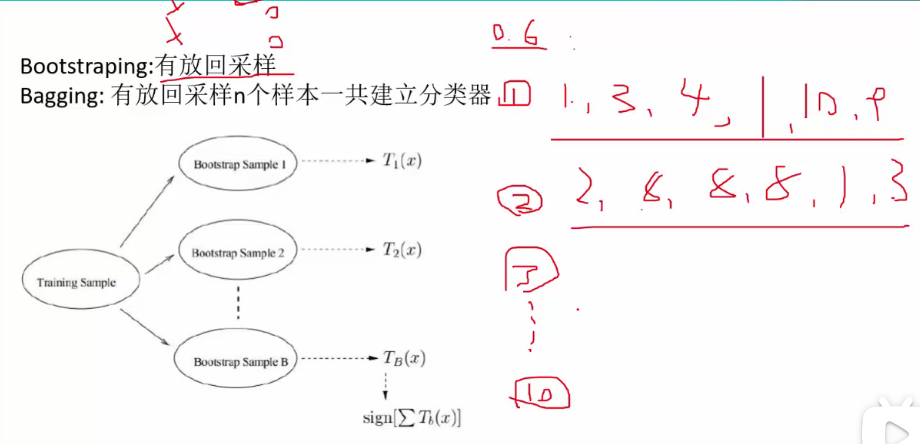
通过建立n棵决策树,进行分类(取众数)和回归(取均值)任务。
2.2随机森林的两重随机性:
拟解决问题:过拟合问题?
解决办法:随机森林通过行采样、列采样对数据进行二次采样,两重随机采样的过程保证了随机性,不会出现过拟合,随机森林一般无需剪枝。
样本选择的随机性(行采样的随机性):例如从含有N个样本中,有放回的随机采样60%。
特征选择的随机性(列选择的随机性):例如从n个特征中选择f个(0<f<=n)。
【注】有放回采样:如样本集合为[1,2,3,4,5,6,7,8,9,10],有放回选择6个[1,1,2,3,4,4]
2.2:详细请参考博客https://blog.csdn.net/yangyin007/article/details/82385967
2.3:详细请参考博客https://blog.csdn.net/weixin_42156897/article/details/94025136




