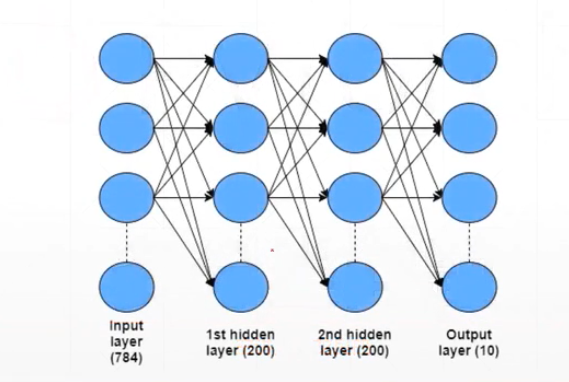
16:交叉熵

1:交叉熵 cross entropy 

(1)entropy熵

 

[注]熵又称为不确定性或者惊喜度或者是信息量.值越小,不确定性越强.(值越小惊喜度越大或者是值越小信息量越大)

例如:下图中的彩票中奖率.

假如1:有四个数字中奖概率分别为0.25,则熵值会很大.即中奖的概率确定性很高,也即是惊喜度越小.

假如2:四个数字,4中奖的概率为0.7,其它三个中奖的概率为0.1,则熵值会比假设1的熵值小,因为中奖的不确定性增加,也即是惊喜度增加.

 (2)cross entropy交叉熵

 

 [注]Dkl称为相对熵,又称为KL散度或信息散度,是两个概率分布间差异的非对称性度量.

设P(x),Q(x)为随机变量X上的两个概率分布,则在离散和连续随机变量的情形下,相对熵的定义分别为:KL(P||Q)=ΣP(x)log P(x)/Q(x)

KL(P||Q)=∫P(x)log P(x)/Q(x) dx

 [注]

当P=Q时,交叉熵等于熵

当采用0,1编码(二分类),p的熵H(p)=0,则H(p,q)=Dkl(p||q),此时当预测值q越接近真实值p,Dkl(p||q)越接近0.反过来,当Dkl(p||q)越接近0,则预测值越接近真实值.故当对二分类进行优化时,其实是将H(p,q)值逼近于0.

(3)交叉熵优化二分类问题

 

 [注]上图中的P(i)=y即真实值.Q(i)=p(i)为预测值

例如:

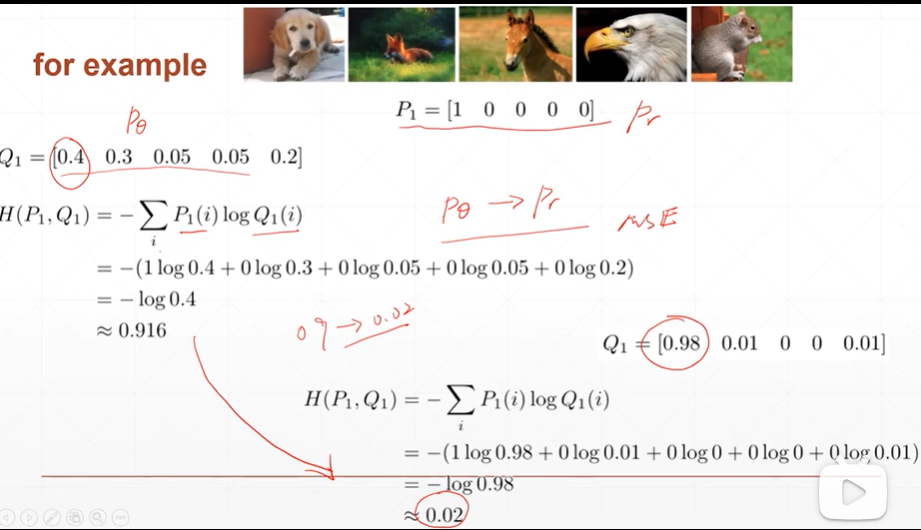
 (4)对于分类问题为什么一般不用sigmoid+MSE(均方差),而使用sigmoid+CEL(cross entropy loss).sigmoid+MSE更适用于回归(regression)问题.

 [注]MSE不适用于二分类的原因:当预测值更接近1时,会出现梯度消失的现象;当预测值更加靠近梯度下降很快的点时,loss会很大,会导致收敛过快.

 [注]但是有时sigmoid+MSE也适用于分类问题,例如:meta-learning(元学习)含义为学会学习.

(5)pytorch中如何实现交叉熵在二分类中的应用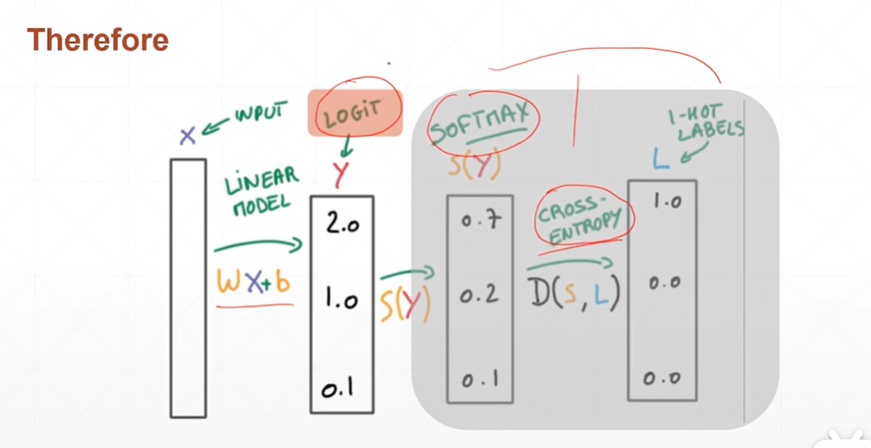

 

 

 

 [注]pytorch中cross_entropy(logits,y)函数已经将softmax和cross entropy打包在了一起.这里的logits一定是未经过激活函数的预测值.

F.cross_entropy()这一步=F.softmax()+torch.log()+nll_loss()这三步.

 2：交叉熵优化多分类问题