SVC和SVR
SVC和SVR
我们可以发现,在sklearn的SVM中有sklearn.svm.SVC()和sklearn.svm.SVR()两个方法,他们对应的其实是SVM在分类和回归两种问题下的结构:
- support vector classify(SVC)支持分类机做二分类的,找出分类面,解决分类问题
- support vector regression(SCR)支持回归机做曲线拟合、函数回归 ,做预测,温度,天气,股票
- 这些都会用于数据挖掘、文本分类、语音识别、生物信息,具体问题具体分析
对于SVC,其实就是我们之前学过的SVM,这里就说一下SVR
知乎这个回答讲的非常好,我这里摘录如下:
简介
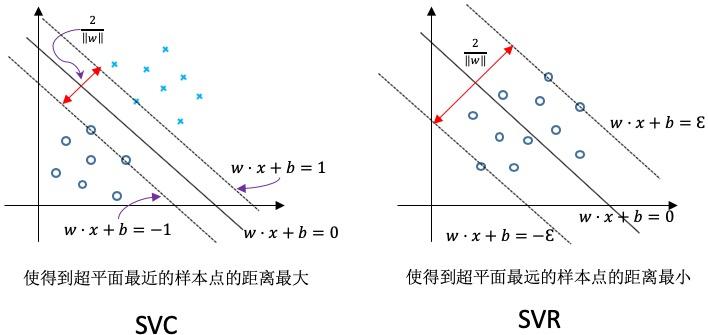
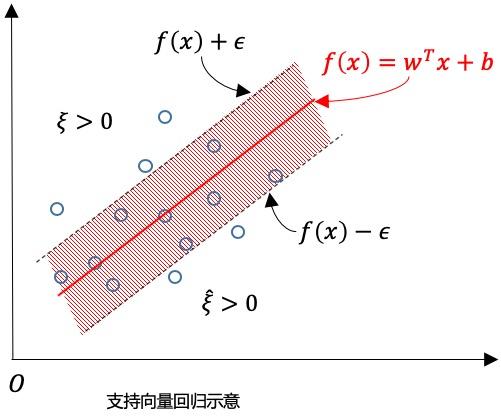
直观上来讲 SVM 分类(SVC Support Vector Classification)与 SVR(Support Vector Regression)图形上的区别如下:
对于样本
,传统的回归模型通常直接输出
与真实输出
之间的差别来计算损失,当且仅当
与
完全相同时,损失才是零。与此不同 SVR 假设我们能容忍
与
之间最多有
的偏差,即仅当
与
之间的差别绝对值大于
时才计算损失。这相当于以
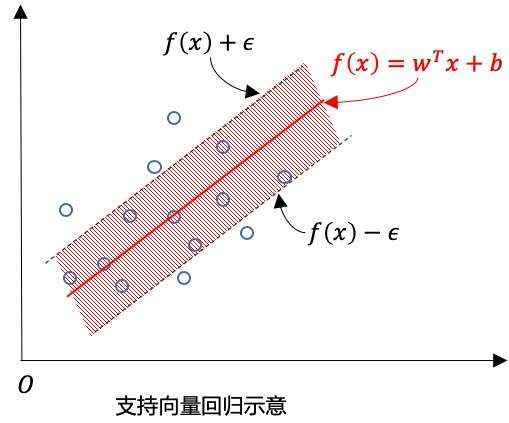
为中心 构建一个宽度为
的间隔带,若样本落入此间隔带,则认为是预测正确的,如下图:
数学形式
【参考】
于是 SVR 问题可以形式化为:
其中 C 正则化常数,
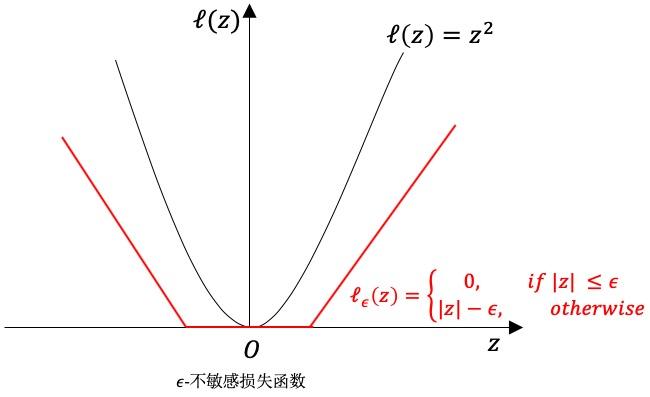
是下图的
ε-不敏感损失(ε-insensitive loss)函数:
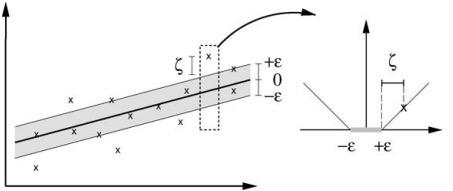
引入松弛变量
和
(间隔两侧的松弛程度有可能不同),可以将式(C2)重写为:
拉格朗日对偶形式
通过引入
,由拉格朗日乘子可以得到式(C3) 的拉格朗日函数:
将
带入上式,并令
的偏导为零,得到:
将式(C5)带入式(C4)可以得到 SVR 的对偶问题:
KKT 与最终决策函数
上述过程满足的 KKT 条件为:
可以看出,当且仅当
时,
能取非零值,当且仅当,
时
能取非零值。换言之,仅当样本
不落入 ε-间隔带中,相应的
和
才能取非零值。此外,约束
与
不能同时成立,因此
和
中至少有一个为零。
将式(C5)第一项带入决策函数,可得最终的决策函数为:
能使上式中
成立的样本即为 SVR 的支持向量,他们必然落在
ε-间隔带之外。显然 SVR 的支持向量仅是训练样本的一部分,即其解仍然具有稀疏性。由 KKT 条件可以看出,对于每个样本
都有
且
,于是在得到
之后,若
则必有
,继而有:
因此,若求解式(C6)得到 \alpha_i 后,理论上说可以任意选取满足
的样本,通过式(C9)求得 b。在实践中采用一种更鲁棒的办法:选择多个(或所有)满足条件
的样本求解 b 后去平均值。
核函数的形式最终的决策函数为:
其中
为核函数。
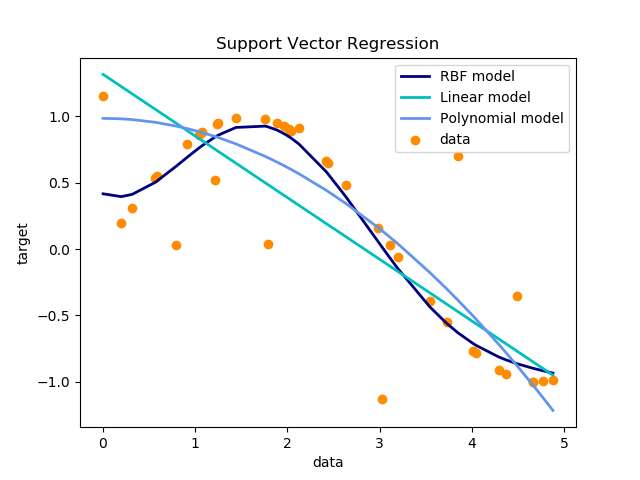
不同核的回归效果
【参考】
下面这一段实践建议我个人觉得也是很中用的:
基于 Sklearn 的实践建议
【参考】
避免数据拷贝
核缓存的大小:对于
SCV、SVR、NuSVC和NuSVR,核函数缓存的大小对于大型问题的运行时间有着非常大的影响。如果有足够多的内存,建议把cache_size的大小设置的尽可能的大。设置 C:1 是一个合理的默认选择,如果有较多噪点数据,你应该较少
C的大小。SVM 算法不是尺度不变,因此强烈建议缩放你的数据。如将输入向量 X 的每个属性缩放到[0,1] 或者 [-1,1],或者标准化为均值为 0 方差为 1 。另外,在测试向量时也应该使用相同的缩放,已获得有意义的结果。
对于
SVC,如果分类的数据不平衡(如有很多的正例很少的负例),可以设置class_weight='balanced',或者尝试不同的惩罚参数C底层实现的随机性:
SVC和NuSVC的底层实现使用了随机数生成器,在概率估计时混洗数据(当probability设置为True),随机性可以通过random_state参数控制。如果probability设置为False,这些估计不是随机的,random_state对结果不在有影响。使用
L1惩罚来产生稀疏解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号