TensorFlow良心入门教程
All the matrials come from Machine Learning class in Polyu,HK and I reorganize them and add reference materials.I promise that I only use them to study and non-proft
.ipynb源文件可通过我的onedrive下载:https://1drv.ms/u/s!Al86h1dThXMNxF-J7FKHKTPkf5yr?e=SAgALh
Warm up
A short example for Tensorflow:
import tensorflow as tf
node1=tf.placeholder(tf.float32)
node2=tf.placeholder(tf.float32)
node3=tf.add(node1,node2)
tf.Session().run(node3,{node1:4,node2:4})
8.0
Basic ideas
It's okay if you don't understand the content well in this section.Section 3rd will be much more detailed and basic
Core TensorFlow constructs
- Dataflow Graphs: entire computation
- Data Nodes: individual data or operations
- Edges: implicit dependencies between nodes
- Operations: any computation
- Constants: single values (tensors)
Choose the place to run code
The whole point of having a dataflow representation is flexibility in choosing location. Tensorflow lets you choose the device to run the code:

Computational graph
A TensorFlow Core programs contains two sections:
Building the computational graph.
Running the computational graph.
So what is a computational graph?
A computational graph is a series of TensorFlow operations arranged into a graph of nodes.
Node
Each node takes zero or more tensors as inputs and produces a tensor as an output.The type of node could be constant,variable,operations and so on.
All nodes return tensors, or higher-dimensional matrices
Tensor
A tensor consists of a set of primitive(原始) values shaped into an array of any number of dimensions.
Variable
To make the model trainable, we need to be able to modify the graph to get new outputs with the same input.So we should use variable:
Variables allow us to add trainable parameters to a graph.They are constructed with a type and initial value.
Placeholder
A placeholder is a promise to provide a value later.
Initializer
To initialize all the variables in a TensorFlow program, tf.global_variables_initializer() is needed.
Model Evaluation and Training
To evaluate the model on training data: loss function
TensorFlow provides optimizers that slowly change each variable in order to minimize the loss function. (In the following example we use gradient descent.)
Session(会话)
To actually evaluate the nodes, we must run the computational graph within a session.
A session encapsulates(封装) the control and state of the TensorFlow runtime.
A linear Rgression Example:
import numpy as np
# Model parameters
W = tf.Variable([.3], dtype=tf.float32)
b = tf.Variable([-.3], dtype=tf.float32)
#Model input and output
x = tf.placeholder(tf.float32)
linear_model = W * x + b #Operator Overloading!
y=tf.placeholder(tf.float32)
#loss
loss=tf.reduce_sum(tf.square(linear_model-y))
#optimizer
optimizer=tf.train.GradientDescentOptimizer(0.01)
train=optimizer.minimize(loss)
#training data
X_train=[1,2,3,4]
y_train=[0,-1,-2,-3]
#training loop
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for i in range(1000):
sess.run(train,{x:X_train,y:y_train})
#evaluate training accuracy
curr_W,curr_b,curr_loss=sess.run([W,b,loss],{x:X_train,y:y_train})
print("W:%s b:%s loss:%s"%(curr_W,curr_b,curr_loss))
W:[-0.9999969] b:[0.9999908] loss:5.6999738e-11
Suggested System Design

Parameter server
it focus:
- Hold Mutable state
- Apply updates
- Maintain availability
- Group Name: ps
Worker
it focus:
- Perform “active” actions
- Checkpoint state to FS
- Mostly stateless; can be restarted
- Group name: worker


The implemnetation of TensorFlow

Distributed Master: compiles the graph, including specialization. Think of it kind of like a query optimizer, but honestly it’s really an impoverished compiler Dataflow executor: the scheduler and coordinator, responsible for invoking kernels on various devices.
Detailed understanding
Introducing Tensors
The term "tensor" in ML,especially tensorflow, has no relation with the term "tensor(called 张量 in Chinese" in physics!
I attach a link which introduces the tensor used in physics and mathematics.After reading it you will find out that maybe google misuse the "tensor"
To understand tensors well, it’s good to have some working knowledge of linear algebra and vector calculus. You already read in the introduction that tensors are implemented in TensorFlow as multidimensional data arrays, but some more introduction is maybe needed in order to completely grasp tensors and their use in machine learning.
Plane Vectors(平面向量)
Please be aware that the content in this section is very very simple
Before you go into plane vectors, it’s a good idea to shortly revise the concept of “vectors”; Vectors are special types of matrices, which are rectangular arrays of numbers. Because vectors are ordered collections of numbers, they are often seen as column matrices(列向量): they have just one column and a certain number of rows. In other terms, you could also consider vectors as scalar(标量) magnitudes that have been given a direction.
Remember: an example of a scalar is “5 meters” or “60 m/sec”, while a vector is, for example, “5 meters north” or “60 m/sec East”. The difference between these two is obviously that the vector has a direction. Nevertheless, these examples that you have seen up until now might seem far off from the vectors that you might encounter when you’re working with machine learning problems. This is normal; The length of a mathematical vector is a pure number: it is absolute. The direction, on the other hand, is relative: it is measured relative to some reference direction and has units of radians or degrees. You usually assume that the direction is positive and in counterclockwise rotation from the reference direction.
Visually, of course, you represent vectors as arrows, as you can see in the picture above. This means that you can consider vectors also as arrows that have direction and length. The direction is indicated by the arrow’s head, while the length is indicated by the length of the arrow.
So what about plane vectors then?
Plane vectors are the most straightforward setup of tensors. They are much like regular vectors as you have seen above, with the sole difference that they find themselves in a vector space. To understand this better, let’s start with an example: you have a vector that is 2 X 1. This means that the vector belongs to the set of real numbers that come paired two at a time. Or, stated differently, they are part of two-space. In such cases, you can represent vectors on the coordinate (x,y) plane with arrows or rays.
Working from this coordinate(坐标) plane in a standard position where vectors have their endpoint at the origin (0,0), you can derive the x coordinate by looking at the first row of the vector, while you’ll find the y coordinate in the second row. Of course, this standard position doesn’t always need to be maintained: vectors can move parallel to themselves in the plane without experiencing changes.
Note that similarly, for vectors that are of size 3 X 1, you talk about the three-space. You can represent the vector as a three-dimensional figure with arrows pointing to positions in the vectors pace: they are drawn on the standard x, y and z axes.
It’s nice to have these vectors and to represent them on the coordinate plane, but in essence(本质), you have these vectors so that you can perform operations on them and one thing that can help you in doing this is by expressing your vectors as bases or unit vectors(单位向量).
Unit vectors are vectors with a magnitude(大小) of one. You’ll often recognize the unit vector by a lowercase letter with a circumflex, or “hat”. Unit vectors will come in convenient if you want to express a 2-D or 3-D vector as a sum of two or three orthogonal components, such as the x− and y−axes, or the z−axis.
And when you are talking about expressing one vector, for example, as sums of components, you’ll see that you’re talking about component vectors, which are two or more vectors whose sum is that given vector.
(now the very very easy part ends)
Tensors
Next to plane vectors, also covectors and linear operators are two other cases that all three together have one thing in common: they are specific cases of tensors. You still remember how a vector was characterized in the previous section as scalar magnitudes that have been given a direction. A tensor, then, is the mathematical representation of a physical entity that may be characterized by magnitude and multiple directions.
And, just like you represent a scalar with a single number and a vector with a sequence of three numbers in a 3-dimensional space, for example, a tensor can be represented by an array of 3^R numbers in a 3-dimensional space.
The “R” in this notation represents the rank of the tensor: this means that in a 3-dimensional space, a second-rank tensor can be represented by 3 to the power of 2 or 9 numbers. In an N-dimensional space, scalars will still require only one number, while vectors will require N numbers, and tensors will require N^R numbers. This explains why you often hear that scalars are tensors of rank 0: since they have no direction, you can represent them with one number.
With this in mind, it’s relatively easy to recognize scalars, vectors, and tensors and to set them apart: scalars can be represented by a single number, vectors by an ordered set of numbers, and tensors by an array of numbers.
What makes tensors so unique is the combination of components and basis vectors(向量基): basis vectors transform one way between reference frames and the components transform in just such a way as to keep the combination between components and basis vectors the same.
This article introduce the "sensor" in physics and mathematics:
source:https://www.jianshu.com/p/2a0f7f7735ad
And this picture summary what is sensor in tensorflow:
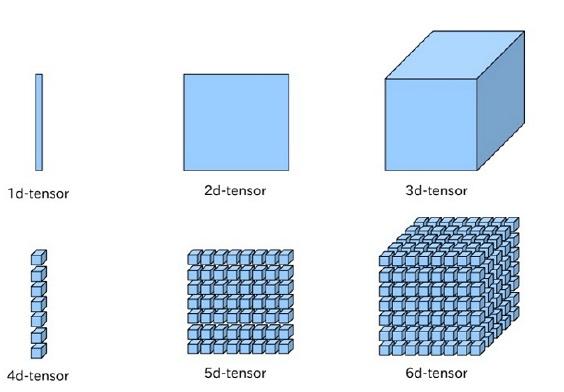
So the sensor in ML actually is just a kind of Multidimensional Arrays
Getting Started With TensorFlow: Basics
You’ll generally write TensorFlow programs, which you run as a chunk; This is at first sight kind of contradictory when you’re working with Python. However, if you would like, you can also use TensorFlow’s Interactive Session, which you can use to work more interactively with the library. This is especially handy when you’re used to working with IPython.
For this tutorial, you’ll focus on the second option: this will help you to get kickstarted with deep learning in TensorFlow. But before you go any further into this, let’s first try out some minor stuff before you start with the heavy lifting.
First, import the tensorflow library under the alias(别名) tf, as you have seen in the previous section. Then initialize two variables that are actually constants. Pass an array of four numbers to the constant() function.
Note that you could potentially also pass in an integer, but that more often than not, you’ll find yourself working with arrays. As you saw in the introduction, tensors are all about arrays! So make sure that you pass in an array 😃 Next, you can use multiply() to multiply your two variables. Store the result in the result variable. Lastly, print out the result with the help of the print() function.
# Import `tensorflow`
import tensorflow as tf
# Initialize two constants
#we usually work with array not integer
x1 = tf.constant([1,2,3,4])
x2 = tf.constant([5,6,7,8])
# Multiply
result = tf.multiply(x1, x2)
# Print the result
print(result)
Tensor("Mul_3:0", shape=(4,), dtype=int32)
Note that you have defined constants above. However, there are two other types of values that you can potentially use, namely placeholders, which are values that are unassigned and that will be initialized by the session when you run it. Like the name already gave away, it’s just a placeholder for a tensor that will always be fed when the session is run; There are also Variables, which are values that can change. The constants, as you might have already gathered, are values that don’t change.
The result of the lines of code is an abstract tensor in the computation graph. However, contrary to what you might expect, the result doesn’t actually get calculated. It just defined the model, but no process ran to calculate the result. You can see this in the print-out: there’s not really a result that you want to see (namely, 30). This means that TensorFlow has a lazy evaluation!
However, if you do want to see the result, you have to run this code in an interactive session. You can do this in a few ways, as is demonstrated below:
# Intialize the Session
sess = tf.Session()
# Print the result
print(sess.run(result))
# Close the session
sess.close()
[ 5 12 21 32]
Note that you can also use the following lines of code to start up an interactive Session, run the result and close the Session automatically again after printing the output:
# Initialize Session and run `result`
#the "with" method will close the session automatically
with tf.Session() as sess:
output = sess.run(result)
print(output)
[ 5 12 21 32]
First Neural Network:Basic Classification
This tutorial trains a neural network model to classify images of clothing, like sneakers and shirts. It's okay if you don't understand all the details, this is a fast-paced overview of a complete TensorFlow program with the details explained as we go.
This tutorial uses tf.keras, a high-level API to build and train models in TensorFlow.
from __future__ import absolute_import, division, print_function
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
1.14.0
Import the Fashion MNIST dataset
This tutorial uses the Fashion MNIST dataset which contains 70,000 grayscale images in 10 categories. The images show individual articles of clothing at low resolution (28 by 28 pixels).
We will use 60,000 images to train the network and 10,000 images to evaluate how accurately the network learned to classify images. You can access the Fashion MNIST directly from TensorFlow, just import and load the data:
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# show the type and size
print(type(train_images),train_images.size)
<class 'numpy.ndarray'> 47040000
Loading the dataset returns four NumPy arrays:
The train_images and train_labels arrays are the training set—the data the model uses to learn.
The model is tested against the test set, the test_images, and test_labels arrays.
The images are 28x28 NumPy arrays, with pixel values ranging between 0 and 255.(yes,no color,just grayscale value) The labels are an array of integers, ranging from 0 to 9. These correspond to the class of clothing the image represents:
- 0 - T-shirt/top
- 1 - Trouser
- 2 - Pullover
- 3 - Dress
- 4 - Coat
- 5 - Sandal
- 6 - Shirt
- 7 - Sneaker
- 8 - Bag
- 9 - Ankle boot
Each image is mapped to a single label. Since the class names are not included with the dataset, store them here to use later when plotting the images:
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
Explore the data
Let's explore the format of the dataset before training the model. The following shows there are 60,000 images in the training set, with each image represented as 28 x 28 pixels:
train_images.shape
(60000, 28, 28)
Likewise, there are 60,000 labels in the training set:
len(train_labels)
60000
Each label is an integer between 0 and 9:
train_labels
array([9, 0, 0, ..., 3, 0, 5], dtype=uint8)
Preprocess the data
The data must be preprocessed before training the network. If you inspect the first image in the training set, you will see that the pixel values fall in the range of 0 to 255:
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()

We scale these values to a range of 0 to 1 before feeding to the neural network model. For this, we divide the values by 255. It's important that the training set and the testing set are preprocessed in the same way:
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)#plot the (i+1)th picture
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()

What is "cmap" in the plt command:
cmap: 颜色图谱(colormap), 默认绘制为RGB(A)颜色空间。plt.cm.binary是使用灰度显示
Build the model
Building the neural network requires configuring the layers of the model, then compiling the model.
Setup the layers
The basic building block of a neural network is the layer. Layers extract representations from the data fed into them. And, hopefully, these representations are more meaningful for the problem at hand.
Most of deep learning consists of chaining together simple layers. Most layers, like tf.keras.layers.Dense, have parameters that are learned during training.
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation=tf.nn.relu),
keras.layers.Dense(10, activation=tf.nn.softmax)
])
The first layer in this network, tf.keras.layers.Flatten, transforms the format of the images from a 2d-array (of 28 by 28 pixels), to a 1d-array of 28 * 28 = 784 pixels. Think of this layer as unstacking rows of pixels in the image and lining them up. This layer has no parameters to learn; it only reformats the data.
After the pixels are flattened, the network consists of a sequence of two tf.keras.layers.Dense layers. These are densely-connected, or fully-connected neural layers. The first Dense layer has 128 nodes (or neurons). The second (and last) layer is a 10-node softmax layer—this returns an array of 10 probability scores that sum to 1. Each node contains a score that indicates the probability that the current image belongs to one of the 10 classes.The first node use"tf.nn.relu",which means ReLu(Rectified Linear Units,线性整流函数),like:

Compile the model
Before the model is ready for training, it needs a few more settings. These are added during the model's compile step:
-
Loss function — This measures how accurate the model is during training. We want to minimize this function to "steer" the model in the right direction.
-
Optimizer — This is how the model is updated based on the data it sees and its loss function.
-
Metrics — Used to monitor the training and testing steps. The following example uses accuracy, the fraction of the images that are correctly classified.
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',metrics=['accuracy'])
Train the model
Training the neural network model requires the following steps:
-
Feed the training data to the model—in this example, the train_images and train_labels arrays.
-
The model learns to associate images and labels.
-
We ask the model to make predictions about a test set—in this example, the test_images array. We verify that the predictions match the labels from the test_labels array.
To start training, call the model. fit method—the model is "fit" to the training data:
model.fit(train_images, train_labels, epochs=10)#epoch means the times of loop
Epoch 1/10
60000/60000 [==============================] - 2s 41us/sample - loss: 2.5657 - acc: 0.7036
Epoch 2/10
60000/60000 [==============================] - 2s 40us/sample - loss: 0.6256 - acc: 0.7659
Epoch 3/10
60000/60000 [==============================] - 2s 39us/sample - loss: 0.5572 - acc: 0.7968
Epoch 4/10
60000/60000 [==============================] - 2s 40us/sample - loss: 0.5327 - acc: 0.8131
Epoch 5/10
60000/60000 [==============================] - 2s 39us/sample - loss: 0.5208 - acc: 0.8183
Epoch 6/10
60000/60000 [==============================] - 2s 40us/sample - loss: 0.4971 - acc: 0.8264
Epoch 7/10
60000/60000 [==============================] - 2s 38us/sample - loss: 0.4906 - acc: 0.8300
Epoch 8/10
60000/60000 [==============================] - 2s 38us/sample - loss: 0.4746 - acc: 0.8337
Epoch 9/10
60000/60000 [==============================] - 2s 39us/sample - loss: 0.4807 - acc: 0.8310
Epoch 10/10
60000/60000 [==============================] - 2s 36us/sample - loss: 0.4641 - acc: 0.8384
<tensorflow.python.keras.callbacks.History at 0x7f1132eccd90>
As the model trains, the loss and accuracy metrics are displayed. This model reaches an accuracy of about 0.8 (or 80%) on the training data.
Evaluate accuracy
Next, compare how the model performs on the test dataset:
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)
10000/10000 [==============================] - 0s 21us/sample - loss: 0.5549 - acc: 0.8258
Test accuracy: 0.8258
It turns out, the accuracy on the test dataset is a little less than the accuracy on the training dataset. This gap between training accuracy and test accuracy is an example of overfitting. Overfitting is when a machine learning model performs worse on new data than on their training data.
Make predictions
With the model trained, we can use it to make predictions about some images.
predictions = model.predict(test_images)
Here, the model has predicted the label for each image in the testing set. Let's take a look at the first prediction:
predictions[0]
array([3.0371911e-19, 4.3924773e-21, 0.0000000e+00, 3.8467766e-17,
0.0000000e+00, 3.0567402e-01, 1.3684910e-31, 2.1130694e-01,
7.4550496e-12, 4.8301896e-01], dtype=float32)
A prediction is an array of 10 numbers. These describe the "confidence" of the model that the image corresponds to each of the 10 different articles of clothing. We can see which label has the highest confidence value:
np.argmax(predictions[0])
9
So the model is most confident that this image is an ankle boot, or class_names[9]. And we can check the test label to see this is correct:
test_labels[0]
9
We can graph this to look at the full set of 10 channels
def plot_image(i, predictions_array, true_label, img):
#绘制第i个元素的图片
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)#使用灰度绘图
#选出predictions_array中最大的那个值作为预测的label
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:#选择文字所使用的颜色
color = 'blue'#正确预测就绘制蓝色图
else:
color = 'red'#否则画红色
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
#绘制第i个元素的直方图
predictions_array, true_label = predictions_array[i], true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
#默认使用灰色(#777777)绘制
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
#对于预测列使用红色
thisplot[predicted_label].set_color('red')
#对于正确列使用蓝色,如果预测的就是正确的,那么这一条设置会覆盖上一条,最终显示的就是蓝色;如果不是的话,会显示红蓝两条
thisplot[true_label].set_color('blue')
i = 0#显示第0个元素
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()

i = 12#打印第12个元素,这个是判断错误的情况
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()

Let's plot several images with their predictions. Correct prediction labels are blue and incorrect prediction labels are red. The number gives the percent (out of 100) for the predicted label. Note that it can be wrong even when very confident.
# Plot the first X test images, their predicted label, and the true label
# Color correct predictions in blue, incorrect predictions in red
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions, test_labels)
plt.show()

Finally, use the trained model to make a prediction about a single image.
# Grab an image from the test dataset
img = test_images[0]
print(img.shape)
(28, 28)
tf.keras models are optimized to make predictions on a batch, or collection, of examples at once. So even though we're using a single image, we need to add it to a list:
# Add the image to a batch where it's the only member.
img = (np.expand_dims(img,0))
print(img.shape)
(1, 28, 28)
Now predict the image:
predictions_single = model.predict(img)
print(predictions_single)
[[3.0371911e-19 4.3924607e-21 0.0000000e+00 3.8467617e-17 0.0000000e+00
3.0567402e-01 1.3684910e-31 2.1130694e-01 7.4550635e-12 4.8301896e-01]]
plot_value_array(0, predictions_single, test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)

model.predict returns a list of lists, one for each image in the batch of data. Grab the predictions for our (only) image in the batch:
np.argmax(predictions_single[0])
9
And, as before, the model predicts a label of 9.
Another tutorial: The Deep Neural Network in Tensorflow
Load the data
We first start with importing all the required modules like numpy, matplotlib and most importantly Tensorflow.
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
tf.reset_default_graph()#change into a new graph for a new test.
#If you use the same graph multiple times,there will be an error saying that variables already exist.
After importing all the modules we will now learn how we can load data in TensorFlow, which should be pretty straightforward. The only thing that we should take into account is the "one_hot=True" argument, which we'll also find in the line of code below: it converts the categorical class labels to binary vectors.
In one-hot encoding, we convert the categorical data into a vector of numbers. We do this because machine learning algorithms cannot work with categorical data directly. Instead, we generate one boolean column for each category or class. Only one of these columns could take on the value 1 for each sample. That explains the term "one-hot encoding".
But what does such a one-hot encoded data column look like?
For our problem statement, the one hot encoding will be a row vector, and for each image, it will have a dimension of 1 x 10. It's important to note here that the vector consists of all zeros except for the class that it represents. There, we'll find a 1. For example, the hand written digit image that we would plot has a label of 7, so for all the similar images, the one hot encoding vector would be [0 0 0 0 0 0 0 1 0 0].
Now that all of this is clear, it's time to import the data!
data = input_data.read_data_sets('MNIST/',one_hot=True)
Extracting MNIST/train-images-idx3-ubyte.gz
Extracting MNIST/train-labels-idx1-ubyte.gz
Extracting MNIST/t10k-images-idx3-ubyte.gz
Extracting MNIST/t10k-labels-idx1-ubyte.gz
Once we have the training and testing data loaded, we're all set to analyze the data in order to get some intuition about the dataset that we are going to work with for this tutorial!
Analyze the Data
Before we start any heavy lifting, it's always a good idea to check out what the images in the dataset look like. First, we can take a programmatical approach and check out their dimensions. Also, take into account that if we want to explore our images, these have already been rescaled between 0 and 1. That means that we would not need to rescale the image pixels again!
# Shapes of training set
print("Training set (images) shape: {shape}".format(shape=data.train.images.shape))
print("Training set (labels) shape: {shape}".format(shape=data.train.labels.shape))
# Shapes of test set
print("Test set (images) shape: {shape}".format(shape=data.test.images.shape))
print("Test set (labels) shape: {shape}".format(shape=data.test.labels.shape))
Training set (images) shape: (55000, 784)
Training set (labels) shape: (55000, 10)
Test set (images) shape: (10000, 784)
Test set (labels) shape: (10000, 10)
From the above output, we can see that the training data has a shape of 55000 x 784: there are 55,000 training samples each of 784-dimensional vector. Similarly, the test data has a shape of 10000 x 784, since there are 10,000 testing samples.
The 784 dimensional vector is nothing but a 28 x 28 dimensional matrix. That's why we will be reshaping each training and testing sample from a 784 dimensional vector to a 28 x 28 x 1 dimensional matrix in order to feed the samples in to the CNN model.
For simplicity, let's create a dictionary that will have class names with their corresponding categorical class labels.
# Create dictionary of target classes
label_dict = {
0: 'zero',
1: 'one',
2: 'two',
3: 'three',
4: 'four',
5: 'five',
6: 'six',
7: 'seven',
8: 'eight',
9: 'nine',
}
Also, let's take a look at the images in our dataset:
plt.figure(figsize=[5,5])
# Display the first image in training data
plt.subplot(121)
#将数组转换为矩阵
curr_img = np.reshape(data.train.images[0], (28,28))
curr_lbl = np.argmax(data.train.labels[0,:])
plt.imshow(curr_img, cmap='gray')
plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")
# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(data.test.images[0], (28,28))
curr_lbl = np.argmax(data.test.labels[0,:])
plt.imshow(curr_img, cmap='gray')
plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")
Text(0.5, 1.0, '(Label: seven)')

The output of above two plots are one of the sample images from both training and testing data, and these images are assigned a class label of 7 (seven). Similarly, other hand written digit images will have different labels, but similar images will have same labels. This means that all the similar images as above two plots will have a class label of 7.
Data Preprocessing
The images are of size 28 x 28 (or a 784-dimensional vector).
The images are already rescaled between 0 and 1 so we don't need to rescale them again, but to be sure let's visualize an image from training dataset as a matrix. Along with that let's also print the maximum and minimum value of the matrix.
data.train.images[0]
array([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.3803922 , 0.37647063, 0.3019608 ,
0.46274513, 0.2392157 , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.3529412 , 0.5411765 , 0.9215687 ,
0.9215687 , 0.9215687 , 0.9215687 , 0.9215687 , 0.9215687 ,
0.9843138 , 0.9843138 , 0.9725491 , 0.9960785 , 0.9607844 ,
0.9215687 , 0.74509805, 0.08235294, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.54901963,
0.9843138 , 0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 ,
0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 ,
0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 ,
0.7411765 , 0.09019608, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.8862746 , 0.9960785 , 0.81568635,
0.7803922 , 0.7803922 , 0.7803922 , 0.7803922 , 0.54509807,
0.2392157 , 0.2392157 , 0.2392157 , 0.2392157 , 0.2392157 ,
0.5019608 , 0.8705883 , 0.9960785 , 0.9960785 , 0.7411765 ,
0.08235294, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.14901961, 0.32156864, 0.0509804 , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.13333334,
0.8352942 , 0.9960785 , 0.9960785 , 0.45098042, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.32941177, 0.9960785 ,
0.9960785 , 0.9176471 , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.32941177, 0.9960785 , 0.9960785 , 0.9176471 ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.4156863 , 0.6156863 ,
0.9960785 , 0.9960785 , 0.95294124, 0.20000002, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.09803922, 0.45882356, 0.8941177 , 0.8941177 ,
0.8941177 , 0.9921569 , 0.9960785 , 0.9960785 , 0.9960785 ,
0.9960785 , 0.94117653, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.26666668, 0.4666667 , 0.86274517,
0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 ,
0.9960785 , 0.9960785 , 0.9960785 , 0.9960785 , 0.5568628 ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.14509805, 0.73333335,
0.9921569 , 0.9960785 , 0.9960785 , 0.9960785 , 0.8745099 ,
0.8078432 , 0.8078432 , 0.29411766, 0.26666668, 0.8431373 ,
0.9960785 , 0.9960785 , 0.45882356, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.4431373 , 0.8588236 , 0.9960785 , 0.9490197 , 0.89019614,
0.45098042, 0.34901962, 0.12156864, 0. , 0. ,
0. , 0. , 0.7843138 , 0.9960785 , 0.9450981 ,
0.16078432, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.6627451 , 0.9960785 ,
0.6901961 , 0.24313727, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.18823531,
0.9058824 , 0.9960785 , 0.9176471 , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.07058824, 0.48627454, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.32941177, 0.9960785 , 0.9960785 ,
0.6509804 , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.54509807, 0.9960785 , 0.9333334 , 0.22352943, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.8235295 , 0.9803922 , 0.9960785 ,
0.65882355, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.9490197 , 0.9960785 , 0.93725497, 0.22352943, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.34901962, 0.9843138 , 0.9450981 ,
0.3372549 , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.01960784,
0.8078432 , 0.96470594, 0.6156863 , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.01568628, 0.45882356, 0.27058825,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ], dtype=float32)
np.max(data.train.images[0])
0.9960785
np.min(data.train.images[0])
0.0
Let us reshape the images so that it's of size 28 x 28 x 1, and feed this as an input to the network.
# Reshape training and testing image
train_X = data.train.images.reshape(-1, 28, 28, 1)
#-1代表的含义是不用我们自己指定这一维的大小,函数会自动计算,但列表中只能存在一个-1
test_X = data.test.images.reshape(-1,28,28,1)
train_X.shape, test_X.shape
((55000, 28, 28, 1), (10000, 28, 28, 1))
We need not reshape the labels since they already have the correct dimensions, but let us put the training and testing labels in separate variables and also print their respective shapes just be on the safer side.
train_y = data.train.labels
test_y = data.test.labels
train_y.shape, test_y.shape
((55000, 10), (10000, 10))
The Deep Neural Network
We'll use three convolutional layers:
The first layer will have 32 "3 x 3" filters, The second layer will have 64 "3 x 3" filters and The third layer will have 128 "3 x 3" filters. In addition, there are three max-pooling layers each of size 2 x 2.
We start off with defining the training iterations training_iters, the learning rate learning_rate and the batch size batch_size. Keep in mind that all these are hyperparameters and that these don't have fixed values, as these differ for every problem statement.
Nevertheless, here's what we usually can expect:
-
Training iterations indicate the number of times we train our network,
-
It is a good practice to use a learning rate of 1e-3, learning rate is a factor that is multiplied with the weights based on which the weights get updated and this indeed helps in reducing the cost/loss/cross entropy and ultimately in converging or reaching the local optima. The learning rate should neither be too high or too low it should be a balanced rate and
-
The batch size means that our training images will be divided in a fixed batch size and at every batch it will take a fixed number of images and train them(So even in one time of training,multiple batches means the training process will repeat many times. It's recommended to use a batch size in the power of 2, since the number of physical processor is often a power of 2, using a number of virtual processor different from a power of 2 leads to poor performance. Also, taking a very large batch size can lead to memory errors so we have to make sure that the machine we run our code on has sufficient RAM to handle specified batch size.
training_iters = 3#the original one is 200 but it's takes a long long time in my PC.So I change it into 3.
learning_rate = 0.001
batch_size = 128
Network Parameters
Next, we need to define the network parameters. Firstly, we define the number of inputs. This is 784 since the image is initially loaded as a 784-dimensional vector. Later, we will see that how we will reshape the 784-dimensional vector to a 28 x 28 x 1 matrix. Secondly, we'll also define the number of classes, which is nothing else than the number of class labels.
# MNIST data input (img shape: 28*28)
n_input = 28
# MNIST total classes (0-9 digits)
n_classes = 10
Now is the time to use those placeholders, about which we read previously in this tutorial. We will define an input placeholder x, which will have a dimension of None x 784 and the output placeholder with a dimension of None x 10. To reiterate, placeholders allow us to do operations and build our computation graph without feeding in data.
Similarly, y will hold the label of the training images in form matrix which will be a None*10 matrix.
The row dimension is None. That's because you have defined batch_size, which tells placeholders that they will receive this dimension at the time when you will feed in the data to them. Since you set the batch size to 128, this will be the row dimension of the placeholders.
We use none because thet batch size isn't always the real size of x and y at one time,for example we may have 128+1 tuples.So in the second time the number of tuple will be only 1.
#both placeholders are of type float
x = tf.placeholder("float", [None, 28,28,1])
y = tf.placeholder("float", [None, n_classes])
Creating wrappers for simplicity
In our network architecture model, we will have multiple convolution and max-pooling layers. In such cases, it's always a better idea to define convolution and max-pooling functions, so that we can call them as many times we want to use them in our network.
-
In the conv2d() function we pass 4 arguments: input x, weights W, bias b and strides(步长). This last argument is by default set to 1, but we can always play with it to see how the network performs. The first and last stride must always be 1, because the first is for the image-number and the last is for the input-channel (since the image is a gray-scale image which has only one channel). After applying the convolution, you will add bias and apply an activation function that is called Rectified Linear Unit (ReLU).
-
The max-pooling function is simple: it has the input x and a kernel size k, which is set to be 2. This means that the max-pooling filter will be a square matrix with dimensions 2 x 2 and the stride by which the filter will move in is also 2.
We will padding equal to same which ensures that while performing the convolution operations, the boundary pixels of the image are not left out, so padding equal to same will basically adds zeros at the boundaries of the input and allow the convolution filter to access the boundary pixels as well.
Similarly, in max-pooling operation padding equal to same will add zeros. Later, when we will define the weights and the biases we will notice that an input of size 28 x 28 is downsampled to 4 x 4 after applying three max-pooling layers.
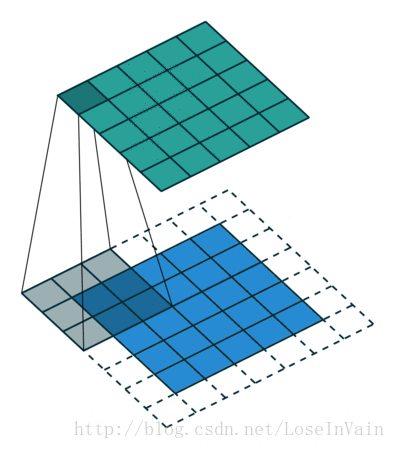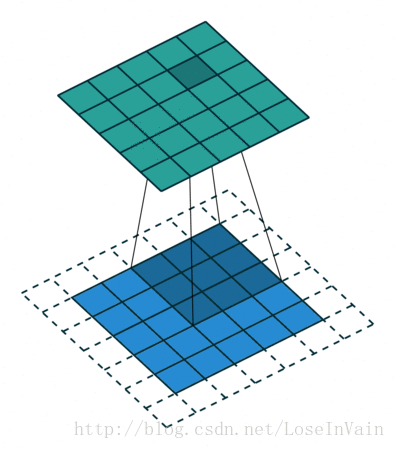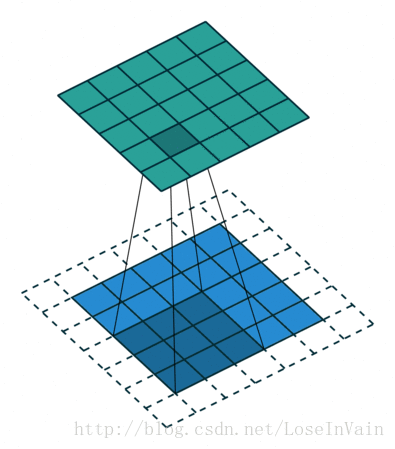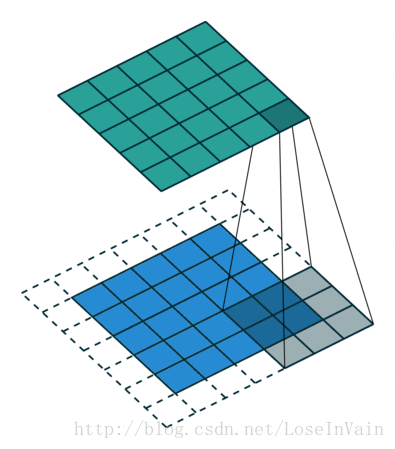
There is an article which explains the "padding" well:https://blog.csdn.net/loseinvain/article/details/78935192
padding是一个字符串输入,分为SAME和VALID分别表示是否需要填充,因为卷积完之后因为周围的像素没有卷积到,因此一般是会出现卷积完的输出尺寸小于输入的现象的,这时候可以利用填充如:
Figure1, No padding, not strides
Figure2, Half padding, not strides
Figure3, No padding, stride 2
Figure4, padding and stride 2
————————————————
版权声明:本文为CSDN博主「FesianXu」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/loseinvain/article/details/78935192
"valid" means "no padding". "same" results in padding the input such that the output has the same length as the original input
def conv2d(x, W, b, strides=1):
#x是节点输入
# Conv2D wrapper, with bias and relu activation
x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
x = tf.nn.bias_add(x, b)
return tf.nn.relu(x) #节点输出
def maxpool2d(x, k=2):
return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1],padding='SAME')
After we have defined the conv2d and maxpool2d wrappers, we can now define our weights and biases variables. So, let's get started!
But first, let's understand each weight and bias parameter step by step. We will create two dictionaries, one for weight and the second for the bias parameter.
-
If we can recall from the above figure that the first convolution layer has 32 "3x3" filters, so the first key (wc1) in the weight dictionary has an argument shape that takes a tuple with 4 values: the first and second are the filter size, while the third is the number of channels in the input image and the last represents the number of convolution filters you want in the first convolution layer. The first key in biases dictionary, bc1, will have 32 bias parameters.
-
Similarly, the second key (wc2) of the weight dictionary has a shape parameter that will take a tuple with 4 values: the first and second again refer to the filter size, and the third represents the number of channels from the previous output. Since we pass 32 convolution filters on the input image, we will have 32 channels as an output from the first convolution layer operation. The last represents the number of filters we want in the second convolution filter. Note that the second key in biases dictionary, bc2, will have 64 parameters.
We will do the same for the third convolution layer.
- Now, it's important to understand the fourth key (wd1). After applying 3 convolution and max-pooling operations, we are downsampling the input image from 28 x 28 x 1 to 4 x 4 x 1 and now we need to flatten this downsampled output to feed this as input to the fully connected layer. That's why we do the multiplication operation 44128 , which is the output of the previous layer or number of channels that are outputted by the convolution layer 3. The second element of the tuple that we pass to shape has number of neurons that we want in the fully connected layer. Similarly, in biases dictionary, the fourth key bd1 has 128 parameters.
We will follow the same logic for the last fully connected layer, in which the number of neurons will be equivalent to the number of classes.
About "tf.contrib.layers.xavier_initializer()":the weight is decided automatically.
This function implements the weight initialization.
This initializer is designed to keep the scale of the gradients roughly the same in all layers. In uniform distribution this ends up being the range: x = sqrt(6. / (in + out)); [-x, x] and for normal distribution a standard deviation of sqrt(2. / (in + out)) is used.
we can see that in the command "'wc1': tf.get_variable('W0', shape=(3,3,1,32), initializer=tf.contrib.layers.xavier_initializer()),",the shape means that our fitters' size is 3*3 and there is 1 channel for the input.And the number of fitters is 32.
The shape in 'wc2' becomes "shape=(3,3,32,64)",which means that the size of fitter is still 3*3,but we have 64 fitters and the number of channels for the input is 32 due to the fitters in the former level.
biases:
every fitter corresponses to a biase for addition in the result.
weights = {
'wc1': tf.get_variable('W0', shape=(3,3,1,32), initializer=tf.contrib.layers.xavier_initializer()),
'wc2': tf.get_variable('W1', shape=(3,3,32,64), initializer=tf.contrib.layers.xavier_initializer()),
'wc3': tf.get_variable('W2', shape=(3,3,64,128), initializer=tf.contrib.layers.xavier_initializer()),
'wd1': tf.get_variable('W3', shape=(4*4*128,128), initializer=tf.contrib.layers.xavier_initializer()),
'out': tf.get_variable('W6', shape=(128,n_classes), initializer=tf.contrib.layers.xavier_initializer()),
}
biases = {
'bc1': tf.get_variable('B0', shape=(32), initializer=tf.contrib.layers.xavier_initializer()),
'bc2': tf.get_variable('B1', shape=(64), initializer=tf.contrib.layers.xavier_initializer()),
'bc3': tf.get_variable('B2', shape=(128), initializer=tf.contrib.layers.xavier_initializer()),
'bd1': tf.get_variable('B3', shape=(128), initializer=tf.contrib.layers.xavier_initializer()),
'out': tf.get_variable('B4', shape=(10), initializer=tf.contrib.layers.xavier_initializer()),
}
Now, it's time to define the network architecture! Unfortunately, this is not as simple as we do it in the Keras framework!
The conv_net() function takes 3 arguments as an input: the input x and the weights and biases dictionaries. Again, let's go through the construction of the network step by step:
-
Firstly, we reshape the 784-dimensional input vector to a 28 x 28 x 1 matrix. As we had seen earlier, the images are loaded as a 784-dimensional vector but we will feed the input to your model as a matrix of size 28 x 28 x 1. The -1 in the reshape() function means that it will infer the first dimension on its own but the rest of the dimension are fixed, that is, 28 x 28 x 1.
-
Next, as shown in the figure of the architecture of the model, we will define conv1 which takes input as an image, weights wc1 and biases bc1. Next, we apply max-pooling on the output of conv1 and we will basically perform a process analogous to this until conv3.
-
Since our task is to classify, given an image it belongs to which class label. So, after we pass through all the convolution and max-pooling layers, we will flatten the output of conv3 to be the input of fully connected neural network. Next, we'll connect the flattened conv3 neurons with each and every neuron in the next layer. Then we will apply activation function on the output of the fully connected layer fc1.
-
Finally, in the last layer, we will have 10 neurons since you have to classify 10 labels. That means we will connect all the neurons of fc1 in the output layer with 10 neurons in the last layer.
def conv_net(x, weights, biases):
# here we call the conv2d function we had defined above and pass the input image x, weights wc1 and bias bc1.
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 14*14 matrix.
conv1 = maxpool2d(conv1, k=2)#k is the size of Window
# Convolution Layer
# here we call the conv2d function we had defined above and pass the input image x, weights wc2 and bias bc2.
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 7*7 matrix.
conv2 = maxpool2d(conv2, k=2)
conv3 = conv2d(conv2, weights['wc3'], biases['bc3'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 4*4.
conv3 = maxpool2d(conv3, k=2)
# Fully connected layer
#'wd1': tf.get_variable('W3', shape=(4*4*128,128), initializer=tf.contrib.layers.xavier_initializer())
#there are 4*4*128*128 weights within the 'wd1',so we can see that there are 4*4*128 nodes in the input layer
#and there are 128 nodes in the output layer.
# Reshape conv2 output to fit fully connected layer input
fc1 = tf.reshape(conv3, [-1, weights['wd1'].get_shape().as_list()[0]])
fc1 = tf.add(tf.matmul(fc1, weights['wd1']), biases['bd1'])#calculation process
fc1 = tf.nn.relu(fc1)
# Output, class prediction
#so in this fully connected neural network there is only one input layer,one hidden layer and one output layer,
# finally we multiply the fully connected layer with the weights and add a bias term.
out = tf.add(tf.matmul(fc1, weights['out']), biases['out'])
return out
weights['wd1'].get_shape().as_list()
[2048, 128]
weights['wd1'].get_shape().as_list()[0]] means find the number of nodes in the input layer
-1 means that it will infer the first dimension on its own but the rest of the dimension are fixed.In this example the dimensions are 1x2048
Loss and Optimizer Nodes
We will start with constructing a model and call the conv_net() function by passing in input x, weights and biases. Since this is a multi-class classification problem, we will use softmax activation on the output layer. This will give us probabilities for each class label. The loss function we use is cross entropy.
The reason we use cross entropy as a loss function is because the cross-entropy function's value is always positive, and tends toward zero as the neuron gets better at computing the desired output, y, for all training inputs, x. These are both properties we would intuitively expect for a cost function. It avoids the problem of learning slowing down which means that if the weights and biases are initialized in a wrong fashion even then it helps in recovering faster and does not hamper much the training phase.
In TensorFlow, we define both the activation and the cross entropy loss functions in one line. We pass two parameters which are the predicted output and the ground truth label y. We will then take the mean (reduce_mean) over all the batches to get a single loss/cost value.
Next, we define one of the most popular optimization algorithms: the Adam optimizer. We can read more about the optimizer from here and we specify the learning rate with explicitly stating minimize cost that we had calculated in the previous step.
There is one picture which compares different optimization algorithms well,which comes from:https://zhuanlan.zhihu.com/p/32626442
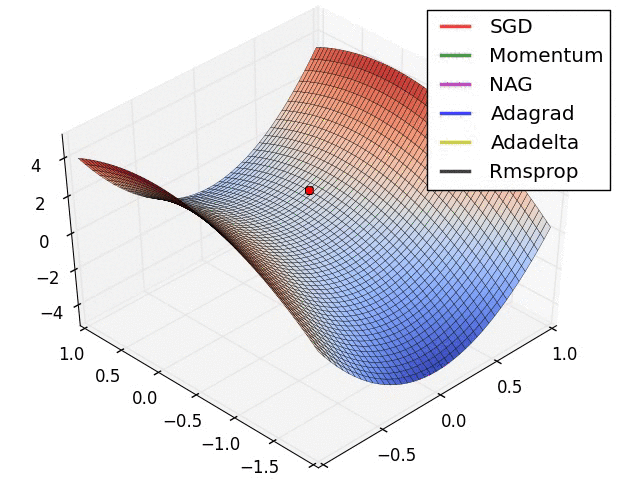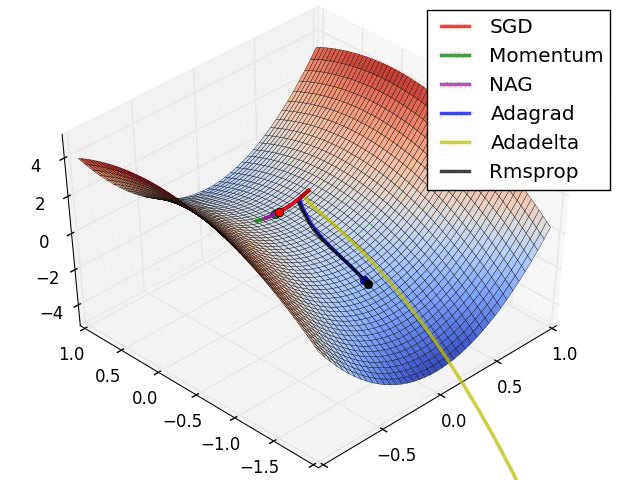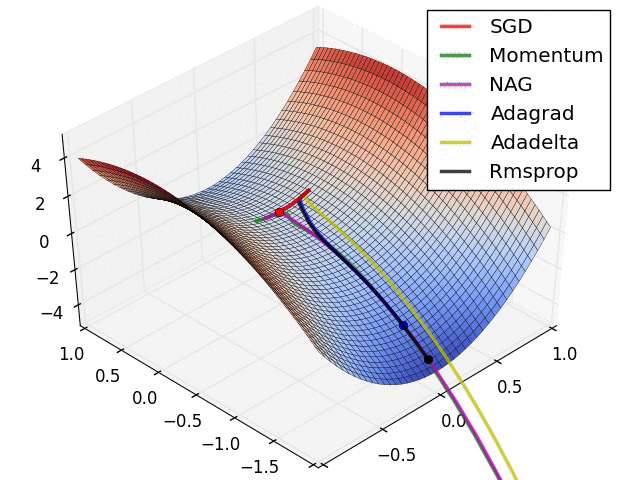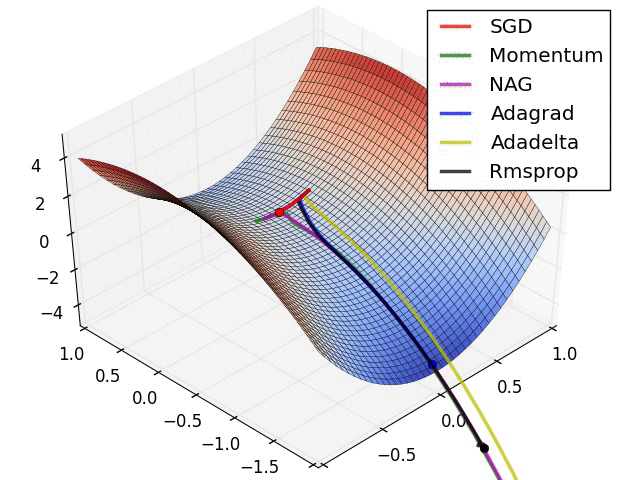
pred = conv_net(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
WARNING:tensorflow:From <ipython-input-45-989f812044df>:3: softmax_cross_entropy_with_logits (from tensorflow.python.ops.nn_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Future major versions of TensorFlow will allow gradients to flow
into the labels input on backprop by default.
See `tf.nn.softmax_cross_entropy_with_logits_v2`.
Evaluate Model Node
To test our model, let's define two more nodes: correct_prediction and accuracy. It will evaluate your model after every training iteration which will help us to keep track of the performance of our model. Since after every iteration the model is tested on the 10,000 testing images, it will not have seen in the training phase.
We can always save the graph and run the testing part later as well. But for now, we will test within the session.
#Here you check whether the index of the maximum value of the predicted image is equal to the actual labelled image. and both will be a column vector.
correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
#calculate accuracy across all the given images and average them out.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
Remember that your weights and biases are variables and that you have to initialize them before you can make use of them. So let's do that with the following line of code:
# Initializing the variables
init = tf.global_variables_initializer()
Training and Testing the Model
When we train and test our model in TensorFlow, we go through the following steps:
-
We start off with launching the graph. This is a class that runs all the TensorFlow operations and launches the graph in a session. All the operations have to be within the indentation.
-
Then, we run the session, which will execute the variables that were initialized in the previous step and evaluates the tensor.
-
Next, we define a for loop that runs for the number of training iterations we had specified in the beginning. Right after that, we'll initiate a second for loop, which is for the number of batches that we will have based on the batch size we chose, so we divide the total number of images by the batch size.
-
We will then input the images based on the batch size you pass in batch_x and their respective labels in batch_y.
-
Now is the most important step. Just like we ran the initializer after creating the graph, now we feed the placeholders x and y the actual data in a dictionary and run the session by passing the cost and the accuracy that we had defined earlier. It returns the loss (cost) and accuracy.
-
We can print the loss and training accuracy after each epoch (training iteration) is completed.
After each training iteration is completed, we run only the accuracy by passing all the 10000 test images and labels. This will give us an idea of how accurately our model is performing while it is training.
It's usually recommended to do the testing once our model is trained completely and validate only while it is in training phase after each epoch. However, let's stick with this approach for now.
How to Visualize the graph
tf.summary.FileWriter() could help us:tf.summary.FileWriter(path, sess.graph) write the graph into the path we given.
We can see the graph by tensorboard,a tool to assist tensorflow.Open the termial and input tensorboard --logdir <dir> to activate tensorboard.<dir>is the path you write on the tf.summary.FileWriter():
with tf.Session() as sess:
sess.run(init)#run the session
train_loss = []
test_loss = []
train_accuracy = []
test_accuracy = []
summary_writer = tf.summary.FileWriter('//home/jiading/OneDrive/', sess.graph)#output the log
for i in range(training_iters):
for batch in range(len(train_X)//batch_size):#take apart and input a batch everytime
batch_x = train_X[batch*batch_size:min((batch+1)*batch_size,len(train_X))]
#min((batch+1)*batch_size,len(train_X)) is used for the last batch where the number of element is likely to be less than the size of batch
batch_y = train_y[batch*batch_size:min((batch+1)*batch_size,len(train_y))]
# Run optimization op (backprop).
# Calculate batch loss and accuracy,initilaize feed_dict where stores all the data needed
opt = sess.run(optimizer, feed_dict={x: batch_x,
y: batch_y})
loss, acc = sess.run([cost, accuracy], feed_dict={x: batch_x,
y: batch_y})
print("Iter " + str(i) + ", Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy for all 10000 mnist test images
test_acc,valid_loss = sess.run([accuracy,cost], feed_dict={x: test_X,y : test_y})
train_loss.append(loss)
test_loss.append(valid_loss)
train_accuracy.append(acc)
test_accuracy.append(test_acc)
print("Testing Accuracy:","{:.5f}".format(test_acc))
summary_writer.close()
Iter 0, Loss= 0.016741, Training Accuracy= 1.00000
Optimization Finished!
Testing Accuracy: 0.97230
Iter 1, Loss= 0.010849, Training Accuracy= 1.00000
Optimization Finished!
Testing Accuracy: 0.98470
Iter 2, Loss= 0.003558, Training Accuracy= 1.00000
Optimization Finished!
Testing Accuracy: 0.98610
The test accuracy looks impressive. It turns out that our classifier does better than the benchmark that was reported, which is an SVM classifier with mean accuracy of 0.897. Also, the model does well compared to some of the deep learning models mentioned on the GitHub profile of the creators of fashion-MNIST dataset.
However, we saw that the model looked like it was overfitting since the training accuracy is more than the testing accuracy. Are these results really all that good?
Let's put our model evaluation into perspective and plot the accuracy and loss plots between training and validation data:
plt.plot(range(len(train_loss)), train_loss, 'b', label='Training loss')
plt.plot(range(len(train_loss)), test_loss, 'r', label='Test loss')
plt.title('Training and Test loss')
plt.xlabel('Epochs ',fontsize=16)
plt.ylabel('Loss',fontsize=16)
plt.legend()
plt.figure()
plt.show()

<Figure size 432x288 with 0 Axes>
plt.plot(range(len(train_loss)), train_accuracy, 'b', label='Training Accuracy')
plt.plot(range(len(train_loss)), test_accuracy, 'r', label='Test Accuracy')
plt.title('Training and Test Accuracy')
plt.xlabel('Epochs ',fontsize=16)#epochs means the time of iterations,which is equal to len(train_loss).
plt.ylabel('Loss',fontsize=16)
plt.legend()
plt.figure()
plt.show()

<Figure size 432x288 with 0 Axes>
From the above two plots, we can see that the test accuracy almost became stagnant after 50-60 epochs and rarely increased at certain epochs. In the beginning, the validation accuracy was linearly increasing with loss, but then it did not increase much.
The validation loss shows that this is the sign of overfitting, similar to test accuracy it linearly decreased but after 25-30 epochs, it started to increase. This means that the model tried to memorize the data and succeeded.
This was it for this tutorial, but there is a task for us all:
-
Our task is to reduce the overfitting of the above model, by introducing dropout technique. For simplicity, we may like to follow along with the tutorial Convolutional Neural Networks in Python with Keras, even though it is in keras, but still the accuracy and loss heuristics are pretty much the same. So, following along with this tutorial will help us to add dropout layers in our current model. Since, both of the tutorial have exactly similar architecture.
-
Secondly, try to improve the testing accuracy, may be by deepening the network a bit, or adding learning rate decay for faster convergence, or try playing with the optimizer and so on!
I believe this tutorial helps us start to understanding how tensorFlow works underneath the hood along with an implementation of convolutional neural networks in Python. If we were able to follow along easily or even with little more efforts, well done!
Try doing some experiments maybe with same model architecture but using different types of public datasets available. You could also try playing with different weight intializers, may be deepen the network architecture, change learning rate etc. and see how your network performs by changing these parameters. But try changing them one at a time only then you will get more intuition about these parameters.
Of course, there is still a lot to cover.
In the end,I paste all the related code in this model here:
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
tf.reset_default_graph()#change into a new graph for a new test.
#If you use the same graph multiple times,there will be an error saying that variables already exist.
data = input_data.read_data_sets('MNIST/',one_hot=True)
# Create dictionary of target classes
label_dict = {
0: 'zero',
1: 'one',
2: 'two',
3: 'three',
4: 'four',
5: 'five',
6: 'six',
7: 'seven',
8: 'eight',
9: 'nine',
}
# Reshape training and testing image
train_X = data.train.images.reshape(-1, 28, 28, 1)
#-1代表的含义是不用我们自己指定这一维的大小,函数会自动计算,但列表中只能存在一个-1
test_X = data.test.images.reshape(-1,28,28,1)
train_y = data.train.labels
test_y = data.test.labels
training_iters = 3#the original one is 200 but it's takes a long long time in my PC.So I change it into 3.
learning_rate = 0.001
batch_size = 128
# MNIST data input (img shape: 28*28)
n_input = 28
# MNIST total classes (0-9 digits)
n_classes = 10
#both placeholders are of type float
x = tf.placeholder("float", [None, 28,28,1])
y = tf.placeholder("float", [None, n_classes])
def conv2d(x, W, b, strides=1):
#x是节点输入
# Conv2D wrapper, with bias and relu activation
x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
x = tf.nn.bias_add(x, b)
return tf.nn.relu(x) #节点输出
def maxpool2d(x, k=2):
return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1],padding='SAME')
weights = {
'wc1': tf.get_variable('W0', shape=(3,3,1,32), initializer=tf.contrib.layers.xavier_initializer()),
'wc2': tf.get_variable('W1', shape=(3,3,32,64), initializer=tf.contrib.layers.xavier_initializer()),
'wc3': tf.get_variable('W2', shape=(3,3,64,128), initializer=tf.contrib.layers.xavier_initializer()),
'wd1': tf.get_variable('W3', shape=(4*4*128,128), initializer=tf.contrib.layers.xavier_initializer()),
'out': tf.get_variable('W6', shape=(128,n_classes), initializer=tf.contrib.layers.xavier_initializer()),
}
biases = {
'bc1': tf.get_variable('B0', shape=(32), initializer=tf.contrib.layers.xavier_initializer()),
'bc2': tf.get_variable('B1', shape=(64), initializer=tf.contrib.layers.xavier_initializer()),
'bc3': tf.get_variable('B2', shape=(128), initializer=tf.contrib.layers.xavier_initializer()),
'bd1': tf.get_variable('B3', shape=(128), initializer=tf.contrib.layers.xavier_initializer()),
'out': tf.get_variable('B4', shape=(10), initializer=tf.contrib.layers.xavier_initializer()),
}
def conv_net(x, weights, biases):
# here we call the conv2d function we had defined above and pass the input image x, weights wc1 and bias bc1.
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 14*14 matrix.
conv1 = maxpool2d(conv1, k=2)#k is the size of Window
# Convolution Layer
# here we call the conv2d function we had defined above and pass the input image x, weights wc2 and bias bc2.
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 7*7 matrix.
conv2 = maxpool2d(conv2, k=2)
conv3 = conv2d(conv2, weights['wc3'], biases['bc3'])
# Max Pooling (down-sampling), this chooses the max value from a 2*2 matrix window and outputs a 4*4.
conv3 = maxpool2d(conv3, k=2)
# Fully connected layer
#'wd1': tf.get_variable('W3', shape=(4*4*128,128), initializer=tf.contrib.layers.xavier_initializer())
#there are 4*4*128*128 weights within the 'wd1',so we can see that there are 4*4*128 nodes in the input layer
#and there are 128 nodes in the output layer.
# Reshape conv2 output to fit fully connected layer input
fc1 = tf.reshape(conv3, [-1, weights['wd1'].get_shape().as_list()[0]])
fc1 = tf.add(tf.matmul(fc1, weights['wd1']), biases['bd1'])#calculation process
fc1 = tf.nn.relu(fc1)
# Output, class prediction
#so in this fully connected neural network there is only one input layer,one hidden layer and one output layer,
# finally we multiply the fully connected layer with the weights and add a bias term.
out = tf.add(tf.matmul(fc1, weights['out']), biases['out'])
return out
pred = conv_net(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
#Here you check whether the index of the maximum value of the predicted image is equal to the actual labelled image. and both will be a column vector.
correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
#calculate accuracy across all the given images and average them out.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Initializing the variables
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)#run the session
train_loss = []
test_loss = []
train_accuracy = []
test_accuracy = []
summary_writer = tf.summary.FileWriter('./Output', sess.graph)#output the log
for i in range(training_iters):
for batch in range(len(train_X)//batch_size):#take apart and input a batch everytime
batch_x = train_X[batch*batch_size:min((batch+1)*batch_size,len(train_X))]
#min((batch+1)*batch_size,len(train_X)) is used for the last batch where the number of element is likely to be less than the size of batch
batch_y = train_y[batch*batch_size:min((batch+1)*batch_size,len(train_y))]
# Run optimization op (backprop).
# Calculate batch loss and accuracy,initilaize feed_dict where stores all the data needed
opt = sess.run(optimizer, feed_dict={x: batch_x,
y: batch_y})
loss, acc = sess.run([cost, accuracy], feed_dict={x: batch_x,
y: batch_y})
print("Iter " + str(i) + ", Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy for all 10000 mnist test images
test_acc,valid_loss = sess.run([accuracy,cost], feed_dict={x: test_X,y : test_y})
train_loss.append(loss)
test_loss.append(valid_loss)
train_accuracy.append(acc)
test_accuracy.append(test_acc)
print("Testing Accuracy:","{:.5f}".format(test_acc))
summary_writer.close()






 浙公网安备 33010602011771号
浙公网安备 33010602011771号