参数的标准化和归一化
参数的标准化与归一化
注:中文资料中从英文文献中学习,提到normalization和standardization时候,往往将其翻译为“标准化”和“归一化”。但是很坑的一点是,由于翻译软件也没有很好的区分两者,所以几乎所有人都将两者混为一谈,甚至A文章对于“标准化”和“归一化”翻译的对应和B文章是完全相反的。所以为了以后不发生鸡同鸭讲的问题,本文不再使用这两个词的中文翻译。其实这两个词往往都是用来表示特征缩放(Feature scaling)的四种方法的,只不过这些方法都可以被称为Normalization,而Standardization指的是其中的一种方法.
- 什么是Normalization和Standardization的区别?
Normalization typically means rescales the values into a range of [0,1]. Standardization typically means rescales data to have a mean of 0 and a standard deviation of 1 (unit variance).
就是说,Normalization只是做参数的映射,而不会改变原来的分布;而Standardization则是会在映射的同时改变原有分布为均值为0、标准差为1的,注意,Standardization之后参数不一定在[0,1]间
方法一:min-max normalization
这种方法的一个比较不好的地方是,每次有新的数据加入,都需要重新计算最大值和最小值.但是它不会改变参数原有分布
方法二and三:Z-score Normalization(Standardization)\Mean normalization
这是mean normalization类方法中比较常用的一种,另外一种方法是: 
这是最常见的Normalization方法,适用于属性的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。该种标准化方式要求原始数据的分布可以近似为高斯分布,否则效果会变得很糟糕。[2](能理解吧?改变原有分布了嘛)
这里有一个样例:
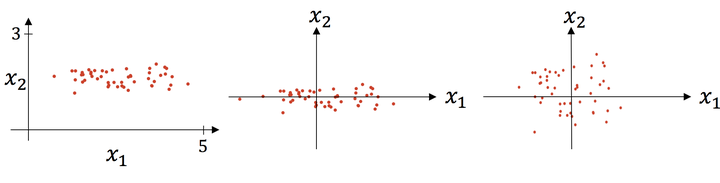
图源:引用4 原图->减去均值->除以标准差
上述两种方法的不同使用场景[2]
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
原因是使用第一种方法(线性变换后),其协方差产生了倍数值的缩放,因此这种方式无法消除量纲对方差、协方差的影响,对PCA分析影响巨大;同时,由于量纲的存在,使用不同的量纲、距离的计算结果会不同。而在第二种归一化方式中,新的数据由于对方差进行了归一化,这时候每个维度的量纲其实已经等价了,每个维度都服从均值为0、方差1的正态分布,在计算距离的时候,每个维度都是去量纲化的,避免了不同量纲的选取对距离计算产生的巨大影响。
————————————————
版权声明:本文为CSDN博主「-柚子皮-」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/pipisorry/article/details/52247379
方法四:Scaling to unit length
这也是常用的一种方法:
这里的向量的范数一般就用欧几里得范数(Euclidean length),但有时也会切换为其他,例如Manhattan Distance, City-Block Length or Taxicab Geometry等
Normalized的效果
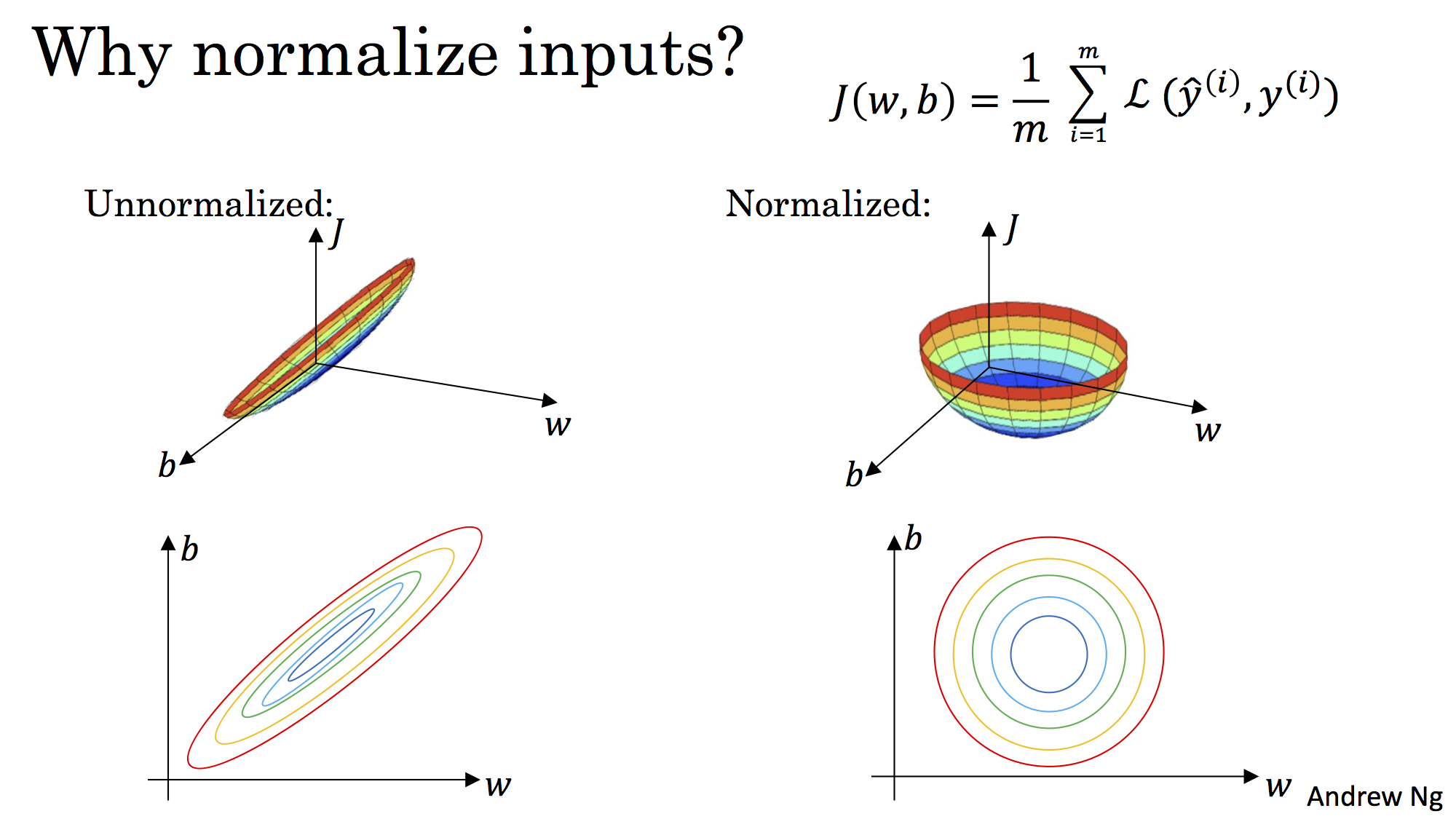
标准化后可以更加容易地得出最优参数
和
以及计算出
的最小值,从而达到加速收敛的效果





 浙公网安备 33010602011771号
浙公网安备 33010602011771号