有偏估计和无偏估计

有偏估计和无偏估计

无偏和有偏

　　本质来讲，无偏/无偏估计是指估算统计量的公式，无偏估计就是可以预见，多次采样计算的统计量（根据估算公式获得）是在真实值左右两边。类似于正态分布的钟型图形。比如对于均值估计：

mean = (1/n)Σxi

　　一定有的比μ大，有的比μ小。

　　那么对于有偏估计，就是多次采样，估算的统计量将会在真实值的一侧（都是大于或者都是小于真实值）。比如对于方差公式：

S² = (1/n)Σ(xi - m)

　　从上面的式子我们可以知道，m是一个固定值，当且仅当m = mean(x)的时候S²取得最小值，这意味着，如果真实值μ ≠ mean(x)，那么必然有σ² < S²，这意味着S²就是一个有偏估计，因为S²都是分布在小于σ²的左侧。

　　另外从数学角度来讲，均值能够保持比较好的无偏性是因为均值计算过程本质还是一个线性过程，这个就是无偏；但是对于方差而言并不是线性模型，所以有偏。

孰优孰劣

　　但是有一点，无偏估计并不一定比有偏估计更加"有效"，因为所谓估算有效是指更加靠近真实值，这个靠近就是通过S²来体现出来，如果统计量估算值虽然有偏，但是更加靠近真实值，那么也是更加有效地；如下图所示：

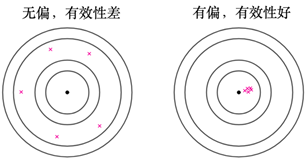
　　左图是无偏的，结果围绕"真实值"，右侧是有偏的，结果偏向于"真实值"一侧，但是毫无疑问有偏的效果更好一些，因为更加接近真实值。

一致性

　　随着样本的增加，S²值将会越来越接近σ²，其实如果样本量非常大，是否有偏已经不重要，因为其实大样本情况下无论是有偏还是无偏，方差都会小到接近真实值。

附录

　　方差的有偏无偏估计

　　无偏估计：

　　S² = (1/n)Σ(x - μ)² ----(1)

　　S² = (1/n-1)Σ(x - mean(x)) -----(2)

　　有偏估计：

　　S² = (1/n)Σ(x - mean(x)) --------(3)

　　请注意(1)和(3)式，只是相差了一个减数，却造成了有偏和无偏，就是因为一个是固定值，一个是不定值（每次采样都不一样）。

　　下面我们来看一下方差无偏公式的推导过程：

参考

https://www.matongxue.com/madocs/808.html 靶图就是参考此篇文章

https://www.matongxue.com/madocs/607.html 这篇文章也是神作，解释清楚了什么是有偏，什么是无偏，另外附录中推导无偏方差的过程就是来自此文

https://spaces.ac.cn/archives/6747 数据科学网站，其中线性和非线性部分就是得子此篇文章，引发了我的对于究竟什么是分布的思考