图论:有向无环图的排序——拓扑排序
图论:有向无环图的排序——拓扑排序
一、什么是拓扑排序
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
有向无环图(DAG)才有拓扑排序,非 DAG 图没有拓扑排序一说。
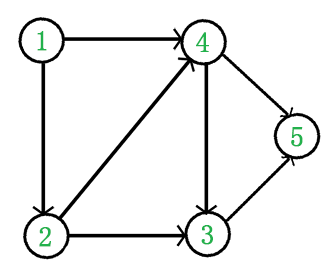
例如,下面这个图:
它是一个 DAG 图,那么如何写出它的拓扑排序呢?这里说一种比较常用的方法:
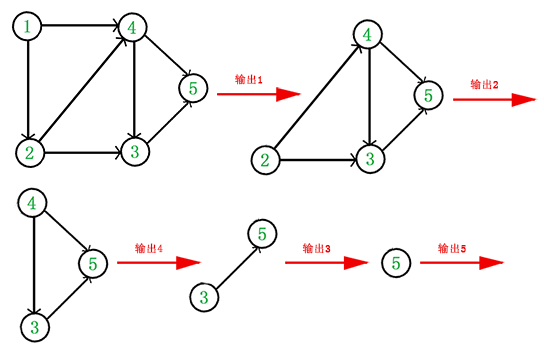
- 从 DAG 图中选择一个 没有前驱(即入度为 0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
于是,得到拓扑排序后的结果是 {1, 2, 4, 3, 5}。
通常,一个有向无环图可以有一个或多个拓扑排序序列。
二、拓扑排序的应用
拓扑排序通常用来 “排序” 具有依赖关系的任务。
比如,如果用一个 DAG 图来表示一个工程,其中每个顶点表示工程中的一个任务,用有向边<A,B><A,B>表示在做任务 B 之前必须先完成任务 A。故在这个工程中,任意两个任务要么具有确定的先后关系,要么是没有关系,绝对不存在互相矛盾的关系(即环路)。
三、拓扑排序的实现
根据上面讲的方法,我们关键是要维护一个入度为 0 的顶点的集合。
图的存储方式有两种:邻接矩阵和邻接表。这里我们采用邻接表来存储图,C++ 代码如下:
#include<iostream>
#include <list>
#include <queue>
using namespace std;
/************************类声明************************/
class Graph
{
int V; // 顶点个数
list<int> *adj; // 邻接表
queue<int> q; // 维护一个入度为0的顶点的集合
int* indegree; // 记录每个顶点的入度
public:
Graph(int V); // 构造函数
~Graph(); // 析构函数
void addEdge(int v, int w); // 添加边
bool topological_sort(); // 拓扑排序
};
/************************类定义************************/
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
indegree = new int[V]; // 入度全部初始化为0
for(int i=0; i<V; ++i)
indegree[i] = 0;
}
Graph::~Graph()
{
delete [] adj;
delete [] indegree;
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
++indegree[w];
}
bool Graph::topological_sort()
{
for(int i=0; i<V; ++i)
if(indegree[i] == 0)
q.push(i); // 将所有入度为0的顶点入队
int count = 0; // 计数,记录当前已经输出的顶点数
while(!q.empty())
{
int v = q.front(); // 从队列中取出一个顶点
q.pop();
cout << v << " "; // 输出该顶点
++count;
// 将所有v指向的顶点的入度减1,并将入度减为0的顶点入栈
list<int>::iterator beg = adj[v].begin();
for( ; beg!=adj[v].end(); ++beg)
if(!(--indegree[*beg]))
q.push(*beg); // 若入度为0,则入栈
}
if(count < V)
return false; // 没有输出全部顶点,有向图中有回路
else
return true; // 拓扑排序成功
}
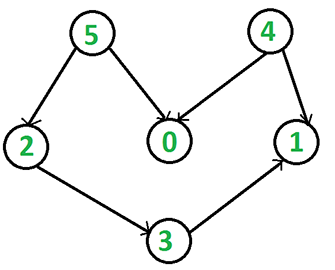
测试如下 DAG 图:
int main()
{
Graph g(6); // 创建图
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
g.topological_sort();
return 0;
}
输出结果是 4, 5, 2, 0, 3, 1。这是该图的拓扑排序序列之一。
每次在入度为 0 的集合中取顶点,并没有特殊的取出规则,随机取出也行,这里使用的queue。取顶点的顺序不同会得到不同的拓扑排序序列,当然前提是该图存在多个拓扑排序序列。
由于输出每个顶点的同时还要删除以它为起点的边,故上述拓扑排序的时间复杂度为O(V+E)O(V+E)。
另外,拓扑排序还可以采用 深度优先搜索(DFS)的思想来实现,详见《topological sorting via DFS》。
拓扑排序的Java实现:
package com.jiading.topo;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;
import java.util.Set;
/**
* 拓扑排序,当前方案并没有在节点类中加入过多的内容
* 但是在图类中加入了边的集合adjaNode
*/
public class TopoSort {
/**
* 拓扑排序节点类
*/
private static class Node {
public Object val;
public int pathIn = 0; // 入度
//因为拓扑排序用不到出度,所以这里就没算出度
public Node(Object val) {
this.val = val;
}
}
/**
* 拓扑图类
*/
private static class Graph {
// 图中节点的集合
public Set<Node> vertexSet = new HashSet<Node>();
// 相邻的节点,纪录边
//key是一个节点,value是一个set用来保存与该节点相连的节点
public Map<Node, Set<Node>> adjaNode = new HashMap<Node, Set<Node>>();
// 将节点加入图中
public boolean addNode(Node start, Node end) {
if (!vertexSet.contains(start)) {
vertexSet.add(start);
}
if (!vertexSet.contains(end)) {
vertexSet.add(end);
}
if (adjaNode.containsKey(start)
&& adjaNode.get(start).contains(end)) {
return false;
}
if (adjaNode.containsKey(start)) {
adjaNode.get(start).add(end);
} else {
Set<Node> temp = new HashSet<Node>();
temp.add(end);
adjaNode.put(start, temp);
}
end.pathIn++;
return true;
}
}
//Kahn算法
private static class KahnTopo {
private List<Node> result; // 用来存储结果集
private Queue<Node> setOfZeroIndegree; // 用来存储入度为0的顶点
private Graph graph;
//构造函数,初始化
public KahnTopo(Graph di) {
this.graph = di;
this.result = new ArrayList<Node>();
this.setOfZeroIndegree = new LinkedList<Node>();
// 对入度为0的集合进行初始化
/**
* 注意如果开始时有多个点的入度为0,拓扑排序并不保证其顺序
*/
for (Node iterator : this.graph.vertexSet) {
if (iterator.pathIn == 0) {
this.setOfZeroIndegree.add(iterator);
}
}
}
//拓扑排序处理过程
private void process() {
while (!setOfZeroIndegree.isEmpty()) {
Node v = setOfZeroIndegree.poll();
// 将当前顶点添加到结果集中
result.add(v);
if (this.graph.adjaNode.keySet().isEmpty()) {
return;
}
// 遍历由v引出的所有边
for (Node w : this.graph.adjaNode.get(v)) {
// 将该边从图中移除,通过减少边的数量来表示
w.pathIn--;
if (0 == w.pathIn) // 如果入度为0,那么加入入度为0的集合
{
setOfZeroIndegree.add(w);
}
}
//从点和边的集合中删去这个点
this.graph.vertexSet.remove(v);
this.graph.adjaNode.remove(v);
}
// 如果此时图中还存在边,那么说明图中含有环路
if (!this.graph.vertexSet.isEmpty()) {
throw new IllegalArgumentException("Has Cycle !");
}
}
//结果集
public Iterable<Node> getResult() {
return result;
}
}
//测试
public static void main(String[] args) {
Node A = new Node("A");
Node B = new Node("B");
Node C = new Node("C");
Node D = new Node("D");
Node E = new Node("E");
Node F = new Node("F");
Graph graph = new Graph();
graph.addNode(A, B);
graph.addNode(B, C);
graph.addNode(B, D);
graph.addNode(D, C);
graph.addNode(E, C);
graph.addNode(C, F);
KahnTopo topo = new KahnTopo(graph);
topo.process();
/**
* 拓扑排序的顺序是由入度为0的点到出度为0的点,当然出度为0的终点是不断减去点之后剩下的,所以这里不记录出度也能找到
*/
for (Node temp : topo.getResult()) {
System.out.print(temp.val.toString() + "-->");
}
}
}
用拓扑排序求最长路径(关键路径)和最短路径
给定一个带权有向无环图及源点 S, 在图中找出从 S 出发到图中其它所有顶点的最长距离。
对于一般的图,求最长路径并不向最短路径那样容易,因为最长路径并没有最优子结构的属性。实际上求最长路径属于 NP-Hard 问题。然而,对于有向无
环图,最长路径问题有线性时间的解。思路与通过使用拓扑排序在线性时间求最短路径 [1] 一样。
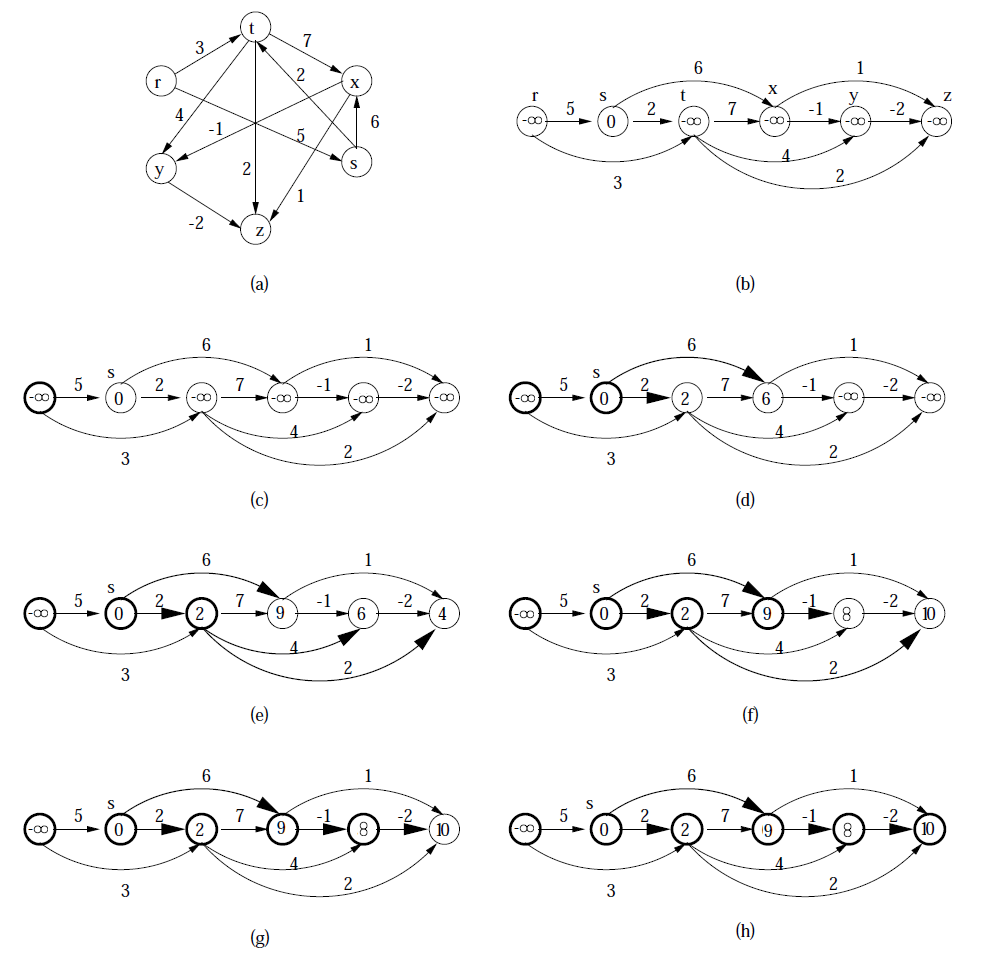
首先初始化到所有顶点的距离为负无穷大,到源点的距离为 0,然后找出拓扑序。图的拓扑排序代表一个图的线性顺序。(图 b 是图 a 的一个线性表示)。
当找到拓扑序后,逐个处理拓扑序中的所有顶点。对于每个被处理的顶点,通过使用当前顶点来更新到它的邻接点的距离。
图 (b) 中,到点 s 的距离初始化为 0, 到其它点的距离初始化为负无穷大,而图 (b) 中的边表示图 (a) 中边的权值。
图 (c) 中,求得从 s 到 r 的距离为负无穷。
图 (d) 中,求得 s 到 t 的最长距离为 2, 到 x 的最长距离为 6。
图 (e) 至图 (h) 依次求得可达点间的最长距离。
下面是寻找最长路径的算法
- 初始化 dist[] = {NINF, NINF, ….} ,dist[s] = 0 。s 是源点,NINF 表示负无穷。dist 表示源点到其它点的最长距离。
- 建立所有顶点的拓扑序列。
- 对拓扑序列中的每个顶点 u 执行下面算法。
对 u 的每个邻接点 v
if (dist[v] < dist[u] + weight(u, v)) ………………………dist[v] = dist[u] + weight(u, v)
下面是 C++ 的实现。
// A C++ program to find single source longest distances in a DAG
#include <iostream>
#include <list>
#include <stack>
#include <limits.h>
#define NINF INT_MIN
using namespace std;
//图通过邻接表来描述。邻接表中的每个顶点包含所连接的顶点的数据,以及边的权值。
class AdjListNode
{
int v;
int weight;
public:
AdjListNode(int _v, int _w) { v = _v; weight = _w;}
int getV() { return v; }
int getWeight() { return weight; }
};
// Class to represent a graph using adjacency list representation
class Graph
{
int V; // No. of vertices’
// Pointer to an array containing adjacency lists
list<AdjListNode> *adj;
// A function used by longestPath
void topologicalSortUtil(int v, bool visited[], stack<int> &Stack);
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int u, int v, int weight);
// Finds longest distances from given source vertex
void longestPath(int s);
};
Graph::Graph(int V) // Constructor
{
this->V = V;
adj = new list<AdjListNode>[V];
}
void Graph::addEdge(int u, int v, int weight)
{
AdjListNode node(v, weight);
adj[u].push_back(node); // Add v to u’s list
}
// 通过递归求出拓扑序列. 详细描述,可参考下面的链接。
// http://www.geeksforgeeks.org/topological-sorting/
void Graph::topologicalSortUtil(int v, bool visited[], stack<int> &Stack)
{
// 标记当前顶点为已访问
visited[v] = true;
// 对所有邻接点执行递归调用
list<AdjListNode>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
AdjListNode node = *i;
if (!visited[node.getV()])
topologicalSortUtil(node.getV(), visited, Stack);
}
// 当某个点没有邻接点时,递归结束,将该点存入栈中。
Stack.push(v);
}
// 根据传入的顶点,求出到到其它点的最长路径. longestPath使用了
// topologicalSortUtil() 方法获得顶点的拓扑序。
void Graph::longestPath(int s)
{
stack<int> Stack;
int dist[V];
// 标记所有的顶点为未访问
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// 对每个顶点调用topologicalSortUtil,最终求出图的拓扑序列存入到Stack中。
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, Stack);
//初始化到所有顶点的距离为负无穷
//到源点的距离为0
for (int i = 0; i < V; i++)
dist[i] = NINF;
dist[s] = 0;
// 处理拓扑序列中的点
while (Stack.empty() == false)
{
//取出拓扑序列中的第一个点
int u = Stack.top();
Stack.pop();
// 更新到所有邻接点的距离
list<AdjListNode>::iterator i;
//能得到从原点到各个点的最长距离
if (dist[u] != NINF)
{
/**
把下面的语句换成
if (dist[i->getV()] > dist[u] + i->getWeight())
dist[i->getV()] = dist[u] + i->getWeight();
求出来的就是最短距离
**/
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (dist[i->getV()] < dist[u] + i->getWeight())
dist[i->getV()] = dist[u] + i->getWeight();
}
}
// 打印最长路径
for (int i = 0; i < V; i++)
(dist[i] == NINF)? cout << "INF ": cout << dist[i] << " ";
}
// Driver program to test above functions
int main()
{
// Create a graph given in the above diagram. Here vertex numbers are
// 0, 1, 2, 3, 4, 5 with following mappings:
// 0=r, 1=s, 2=t, 3=x, 4=y, 5=z
Graph g(6);
g.addEdge(0, 1, 5);
g.addEdge(0, 2, 3);
g.addEdge(1, 3, 6);
g.addEdge(1, 2, 2);
g.addEdge(2, 4, 4);
g.addEdge(2, 5, 2);
g.addEdge(2, 3, 7);
g.addEdge(3, 5, 1);
g.addEdge(3, 4, -1);
g.addEdge(4, 5, -2);
int s = 1;
cout << "Following are longest distances from source vertex " << s <<" \n";
g.longestPath(s);
return 0;
}
输出结果:
从源点1到其它顶点的最长距离
INF 0 2 9 8 10
时间复杂度:拓扑排序的时间复杂度是 O(V+E). 求出拓扑顺序后,对于每个顶点,通过循环找出所有邻接点,时间复杂度为 O(E)。所以内部循环运行 O(V+E) 次。
因此算法总的时间复杂度为 O(V+E)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号