矩阵的奇异值分解（SVD）及其应用

奇异值分解（Singular Value Decomposition, SVD）是矩阵的一种分解方法，与特征值分解不同，它可以应用于长方矩阵中，并将其分解成三个特殊矩阵的乘积。此外SVD分解还具有许多优良的性质，在图像压缩，数据降维和推荐系统等算法中都具有广泛的应用。

奇异值分解的引入

我们考虑二维的情形，考虑一组二维空间上的单位正交向量 \(\boldsymbol{v}_1 , \boldsymbol{v}_2\) ，设任意一个变换矩阵 \(M \in \mathbb R ^ {m \times 2}\) ，对其作变换得到另外一组正交向量 \(M\boldsymbol{v}_1, M\boldsymbol{v}_2\) ，容易知道变换后的正交向量仍然是该二维平面上的一组基底，可以对这组基底进行单位化得到 \(\boldsymbol{u}_1, \boldsymbol{u}_2\)，即单位化前后的向量存在伸缩关系：

\[\begin{cases} \begin{aligned} M\boldsymbol{v}_1 &= \sigma_1 \boldsymbol{u}_1 \\ M\boldsymbol{v}_2 &= \sigma_2 \boldsymbol{u}_2 \\ \end{aligned} \end{cases} \]

此外，对于该二维平面上的任意一个向量 \(\boldsymbol{x} \in \mathbb R^2\) ，可以在基底 \((\boldsymbol{v}_1, \boldsymbol{v}_2)\) 下线性表示为

\[\boldsymbol{x} = (\boldsymbol{v}_1 \cdot \boldsymbol{x}) \boldsymbol{v}_1 + (\boldsymbol{v}_2 \cdot \boldsymbol{x}) \boldsymbol{v}_2 \]

对该向量作上述线性变换，可以得到

\[\begin{aligned} M\boldsymbol{x} &= (\boldsymbol{v}_1 \cdot \boldsymbol{x}) M \boldsymbol{v}_1 + (\boldsymbol{v}_2 \cdot \boldsymbol{x}) M \boldsymbol{v}_2 \\ &= (\boldsymbol{v}_1 \cdot \boldsymbol{x}) \sigma_1 \boldsymbol{u}_1 + (\boldsymbol{v}_2 \cdot \boldsymbol{x}) \sigma_2 \boldsymbol{u}_2 \\ &= \boldsymbol{v}_1 ^ \text T \boldsymbol{x} \ \sigma_1 \boldsymbol{u}_1 + \boldsymbol{v}_2 ^ \text T \boldsymbol{x}\ \sigma_2 \boldsymbol{u}_2 \\ &= \boldsymbol{u}_1 \sigma_1 \boldsymbol{v}_1 ^ \text T \boldsymbol{x} + \boldsymbol{u}_2 \sigma_2 \boldsymbol{v}_2 ^ \text T \boldsymbol{x} \\ &= \begin{pmatrix} \boldsymbol{u}_1 & \boldsymbol{u}_2 \end{pmatrix} \begin{pmatrix} \sigma_1 & \ \\ \ & \sigma_2 \\ \end{pmatrix} \begin{pmatrix} \boldsymbol{v}_1 ^ \text T \\ \boldsymbol{v}_2 ^ \text T \\ \end{pmatrix} \boldsymbol{x} \end{aligned} \]

若定义 \(\boldsymbol{U} = \begin{pmatrix} \boldsymbol{u}_1 & \boldsymbol{u}_2 \end{pmatrix}, \mathbf \Sigma = \begin{pmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ \end{pmatrix}, \boldsymbol{V} ^ \text T = \begin{pmatrix} \boldsymbol{v}_1 ^ \text T \\ \boldsymbol{v}_2 ^ \text T \\ \end{pmatrix}\) ，则对于任一变换矩阵 \(M \in \mathbb R ^ {2 \times 2}\) ，都可以分解成如下两组单位正交基底与对角矩阵的乘积的形式

\[M=\boldsymbol{U} \mathbf \Sigma \boldsymbol{V} ^ \text T \]

一般的，对于任意变换矩阵 \(A \in \mathbb R ^{m \times n}\) ，都存在单位正交阵 \(\boldsymbol{U} \in \mathbb R ^ {m \times m}， \boldsymbol{V} \in \mathbb R ^ {n \times n}\)，类对角矩阵 \(\mathbf \Sigma \in \mathbb R ^{m \times n}\) ，满足

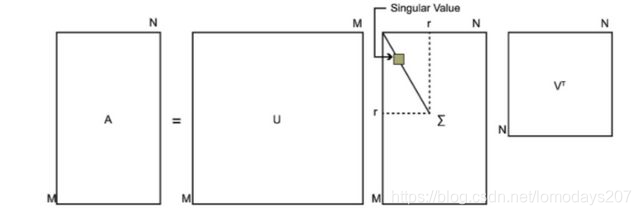
\[A = \boldsymbol{U} \mathbf \Sigma \boldsymbol{V} ^ \text T \]

上式即为矩阵的奇异值分解，其中类对角矩阵 \(\mathbf \Sigma\) 中的非零对角元素称为矩阵 \(A\) 的奇异值，矩阵 \(U,V\) 分别叫做左奇异矩阵和右奇异矩阵（酉矩阵）

奇异值分解的计算

下面考虑如何获取一个长方矩阵的奇异值分解，并给出一个具体的奇异值分解算例。

对于矩阵 \(A \in \mathbb R ^ {m \times n}\) ，我们考察其方阵形式 \(A ^ \text T A\) 和 \(AA ^ \text T\) 。由于 \(A^\text T A\) 是 \(n \times n\) 的实对陈方阵，因此可以对其进行特征值分解。

\[A ^ \text T A = Q \Lambda Q ^ \text T \]

同时，矩阵 \(A\) 存在奇异值分解，即

\[\begin{aligned} A ^ \text T A &= (\boldsymbol{U} \mathbf \Sigma \boldsymbol{V} ^ \text T) ^ \text T \boldsymbol{U} \mathbf \Sigma \boldsymbol{V} ^ \text T \\ &= V \Sigma ^ \text T U ^ \text T U \Sigma V ^ \text T \\ &= V \Sigma ^ \text T \Sigma V ^ \text T \\ &= V \Sigma ^ 2 V ^ \text T \end{aligned} \]

对比上面两式的结果

\[V = Q \\ \Sigma ^ 2 = \Lambda \]

可以发现右奇异矩阵即为 \(A^ \text T A\) 的特征向量矩阵，而所谓的奇异值则为 \(A^\text T A\) 的特征值的算术平方根。
同理可以再考察 \(AA^\text T\) ，即

\[\begin{aligned} AA^\text T &= (U\Sigma V^\text T)(U\Sigma V^\text T)^\text T \\ &= U\Sigma V^\text T V \Sigma ^\text T U ^ \text T \\ &= U \Sigma \Sigma ^ \text T U ^ \text T \end{aligned} \]

可以发现左奇异矩阵即为 \(AA^\text T\) 的特征向量矩阵。因此，要求解矩阵 \(A\) 的奇异值分解，只需分别计算 \(A^\text T A\) 和 \(AA^\text T\) 的特征值分解即可，下面通过一个具体的算例进一步说明。
（算例）计算矩阵 \(A = \begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \\ \end{pmatrix}\)的 SVD 分解。
解：考察 \(A^\text T A\) 和 \(AA^\text T\) ，

\[A^\text T A= \begin{pmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \\ \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \\ \]

\[A A^\text T= \begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ \end{pmatrix} = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1 \\ \end{pmatrix} \\ \]

作特征值分解并单位化特征向量

\[A^\text T A= \begin{pmatrix} \frac{1}{\sqrt 2} & \frac{1}{\sqrt 2} \\ \frac{-1}{\sqrt 2} & \frac{1}{\sqrt 2} \\ \end{pmatrix} \begin{pmatrix} 3 & 0 \\ 0 & 1 \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt 2} & \frac{-1}{\sqrt 2} \\ \frac{1}{\sqrt 2} & \frac{1}{\sqrt 2} \\ \end{pmatrix} \\ \]

\[A A^ \text T= \begin{pmatrix} \frac{1}{\sqrt 6} & \frac{-1}{\sqrt 2} & \frac{1}{\sqrt 3} \\ \frac{2}{\sqrt 6} & 0 & \frac{-1}{\sqrt 3} \\ \frac{1}{\sqrt 6} & \frac{1}{\sqrt 2} & \frac{1}{\sqrt 3} \\ \end{pmatrix} \begin{pmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt 6} & \frac{2}{\sqrt 6} & \frac{1}{\sqrt 6} \\ \frac{-1}{\sqrt 2} & 0 & \frac{1}{\sqrt 2} \\ \frac{1}{\sqrt 3} & \frac{-1}{\sqrt 3} & \frac{1}{\sqrt 3} \\ \end{pmatrix} \]

据此可以得到奇异值 \(\sigma_1 = \sqrt 3, \sigma_2 = 1\) ，则SVD分解为

\[A = \begin{pmatrix} \frac{1}{\sqrt 6} & \frac{-1}{\sqrt 2} & \frac{1}{\sqrt 3} \\ \frac{2}{\sqrt 6} & 0 & \frac{-1}{\sqrt 3} \\ \frac{1}{\sqrt 6} & \frac{1}{\sqrt 2} & \frac{1}{\sqrt 3} \\ \end{pmatrix} \begin{pmatrix} \sqrt 3 & 0 \\ 0 & 1 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt 2} & \frac{-1}{\sqrt 2} \\ \frac{1}{\sqrt 2} & \frac{1}{\sqrt 2} \\ \end{pmatrix} \\ \]

需要注意的一点是，在求解奇异值或者特征值矩阵时，为了方便后续处理，我们一般将特征值或奇异值按大小降序排列，且特征向量一般都做归一化处理。

奇异值分解的几何意义

单位正交矩阵可以看作空间中的旋转矩阵，而对角矩阵则表示沿坐标轴方向上的伸缩变换，因此对于一个矩阵，也可以看作是一种线性变换，所谓的奇异值分解就是将这一变换分解成两次旋转变换和一次沿坐标轴的拉伸变换的过程，更直观的变换过程如下图所示：

奇异值分解的应用

奇异值分解在平面拟合，图像压缩和降噪，主成分分析和推荐系统等算法中都有广泛的应用，下面以直线拟合和图像压缩为例说明。

直线拟合问题

设直线的方程为 \(ax+by+c=0\) ，采集到一组点集 \((x_i, y_i)\) ，需要根据这组点集拟合直线方程。要求解这一问题，可以构建误差函数

\[e_i = ax_i + by_i +c \]

当所有点的误差最小时，即认为拟合效果最好。这本质上是一个线性最小二乘问题，其数学形式可以表示为

\[\begin{aligned} (a,b)^* &= \arg \min \sum_{i=0}^{N}{e_i}^2 \\ &= \arg \min \sum_{i=0}^{N}{(ax_i + by_i + c)^ 2} \end{aligned} \]

构造矩阵 \(A = \begin{pmatrix} x_0 & y_0 & 1 \\ x_1 & y_1 & 1 \\ \vdots & \vdots & \vdots \\ x_N & y_N & 1 \\ \end{pmatrix}, \boldsymbol{x} = \begin{pmatrix} a \\ b \\ c \\ \end{pmatrix}\) ，则可以将上述求解过程写成矩阵形式

\[\begin{aligned} (a,b)^* &= \arg \min (A\boldsymbol{x})^\text T(A\boldsymbol{x}) \\ &= \arg \min \boldsymbol{x}^\text T (A^\text T A)\boldsymbol{x} \\ &= \arg \min \boldsymbol{x} ^ \text T V \Sigma^2 V^\text T \boldsymbol{x} \end{aligned} \]

注意到 \(V^\text T \boldsymbol{x}\) 其实是向量 \(\boldsymbol{x}\) 在基底 \(V\) 下的一组坐标，可以记作 \(\bm \alpha\) ，即

\[V^\text T \boldsymbol{x} = \begin{pmatrix} \boldsymbol{v}_1^\text T \\ \boldsymbol{v}_2^\text T \\ \vdots \\ \boldsymbol{v}_N^\text T \\ \end{pmatrix} \boldsymbol{x} = \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_N \\ \end{pmatrix} = \bm{\alpha} \]

则上式可以进一步写成

\[\begin{aligned} \boldsymbol{x}^\text T V \Sigma^2 V^\text T \boldsymbol{x} &= \bm \alpha^\text T \Sigma^2 \bm \alpha \\ &= \sigma_1^2 \alpha_1^2 + \sigma_2^2 \alpha_2^2 + \cdots + \sigma_N^2 \alpha_N^2 \\ &\ge \sigma_N^2 \end{aligned} \]

在考虑归一化的拟合解前提下，即 \(\bm{\left| x \right|} = 1\) 时，当且仅当坐标 \(\bm \alpha\) 取 \(\begin{pmatrix} 0 & 0 & \cdots & 1 \end{pmatrix}^\text T\) 时取等号，此时求解以下方程

\[\begin{pmatrix} \boldsymbol{v}_1^\text T \\ \boldsymbol{v}_2^\text T \\ \vdots \\ \boldsymbol{v}_N^\text T \\ \end{pmatrix} \boldsymbol x = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \\ \end{pmatrix} \]

容易得到，此时\(\boldsymbol x = \boldsymbol{v}_N\)。也就是说，要求解误差的最小值，只需要进行奇异值分解，取右奇异矩阵的最后一维作为解 \(\bm{x}\) 即可，此时对应的拟合误差即为 \(\sigma_N^2\) ，也就是在最小二乘意义下的最小误差。
下面通过一个直线拟合的编程实例来进一步说明上述结论。
（编程实例）考虑直线 \(x + 2y + 5 = 0\) ，给定一系列带有噪声的点集，根据这组点集拟合直线，并与真值对比，得到拟合参数的均方误差。
采用C++语言编写程序，调用Eigen线性代数库进行SVD分解，代码如下：

Eigen::Vector3d abc = Eigen::Vector3d(1, 2, 5).normalized();    // 直线参数真值
const double sigma = 0.6;   // 噪声方差
const size_t count = 15;    // 取样点的个数
// 利用 OpenCV 的随机数种子生成取样点
cv::RNG rng;
Eigen::MatrixXd A(count, 3);
for(size_t i=0; i<count; ++i) {
    A.row(i) << i, -(abc[0]/abc[1])*i - (abc[2]/abc[1]) + rng.gaussian(sigma), 1;
}
// SVD求解, 并取出 V 矩阵的最后一维作为拟合解 x
Eigen::VectorXd x = Eigen::JacobiSVD<Eigen::MatrixXd>(A, Eigen::ComputeThinV).matrixV().col(2);
// 输出求解结果
cout << "==> true value: abc = " << abc.transpose() << endl;        // 打印真值
cout << "==> svd solving result: x = " << x.transpose() << endl;    // 打印拟合参数
cout << "   ==> error RMS = " << sqrt( (A*x).squaredNorm() / double(count) ) << endl;   // 打印均方误差

程序运行结果截图为：

注意SVD分解时考虑的是归一化的向量，因此得到的也是归一化后的拟合结果，与实际直线参数之间差了一个比例系数。
可以看到在噪声方差为0.6，取样点数为15个点时，得到的拟合结果的均方误差为0.2，拟合结果基本可以接受，在噪声方差更小的情况下，可以得到更可靠的拟合结果。

图像压缩问题

考虑一个 \(m \times n\) 的矩阵 \(A\) ，其奇异值分解式为

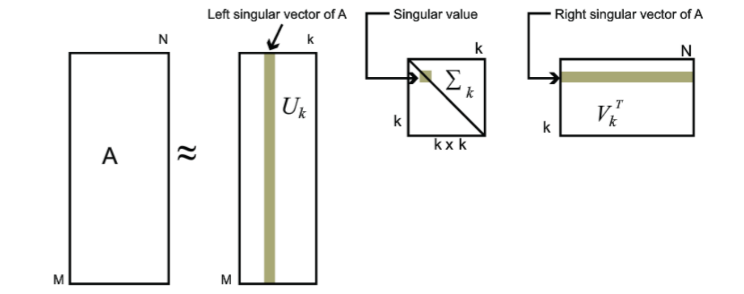
\[A=U_{m \times m}\Sigma_{m\times n} V_{n \times n}^\text T \]

我们发现求得的奇异值衰减速度较快，前面几项的奇异值较大，而越往后的奇异值则越小，也就是说我们可以通过只保留前面几项奇异值来对 \(A\) 进行近似，这种做法可以压缩存储空间，在图像处理领域有着广泛的应用。具体做法是我们可以取出前 \(k\) 个奇异值，得到近似的 \(\tilde A\) ，其中 \(\frac{k}{\min\{m,n\}}\) 称为矩阵的压缩比。

\[A \approx \tilde A = U_{m \times k} \Sigma_{k \times k} V_{k \times n}^\text T \]

（编程实例）给定一张图片（如下），考虑采用不同的压缩比对其进行压缩，并对比分析压缩效果。

采用C++语言编写程序，调用OpenCV图像处理库来进行图像矩阵的SVD分解，采用不同的压缩比（0.01, 0.05, 0.1, 0.2, 0.3, 0.5）重复执行程序，得到输出结果。程序代码如下：

// 读入图像
cv::Mat img_original = cv::imread("../image.png", cv::IMREAD_GRAYSCALE);
cv::Mat img = img_original.clone();
img.convertTo(img, CV_64FC1, 1/255.0);
// 对图像进行SVD分解
cv::Mat U, Vt, W;
cv::SVD::compute(img, W, U, Vt);
// 图像压缩操作
int rank = min(img.rows, img.cols);
cv::Mat W_hat = cv::Mat(rank, rank, CV_64FC1, cv::Scalar(0));  // 取前k维的奇异值矩阵
double compression_ratio = 0.3;     // 设定压缩比
int k = rank * compression_ratio;
for(size_t i=0; i<k; ++i) {
    W_hat.at<double>(i, i) = W.at<double>(i, 0);
}
cv::Mat img_compression = U * W_hat * Vt;   // 计算压缩后的图像
// 压缩图像输出
img_compression.convertTo(img_compression, CV_8UC1, 255.0);
cv::imwrite("./ratio=0_3.png", img_compression);

输出压缩结果如下所示