hdu 5120 Intersection 两个圆的面积交
Intersection
Time Limit: 4000/4000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)
Problem Description
Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.

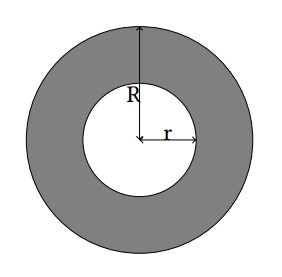
A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.

Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.
Input
The first line contains only one integer T (T ≤ 105), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).
Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.
Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.
Output
For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.
Sample Input
2
2 3
0 0
0 0
2 3
0 0
5 0
Sample Output
Case #1: 15.707963
Case #2: 2.250778
Source
题意:求两个圆环的面积交;
思路:圆环的面积交=大圆面积交-2*大小圆面积交+小圆面积交;
#include<bits/stdc++.h> using namespace std; #define LL long long #define fi first #define se second #define mkp make_pair #define eps 1e-8 const double pi=acos(-1); const int N=2e5+60,M=1e6+10,inf=1e9+10; const LL INF=1e18+10,mod=19260817; int sgn(double x) { if(fabs(x) < eps)return 0; if(x < 0)return -1; else return 1; } struct Point { double x,y; Point() {} Point(double _x,double _y) { x = _x; y = _y; } Point operator -(const Point &b)const { return Point(x - b.x,y - b.y); } //叉积 double operator ^(const Point &b)const { return x*b.y - y*b.x; } //点积 double operator *(const Point &b)const { return x*b.x + y*b.y; } //绕原点旋转角度B(弧度值),后x,y的变化 void transXY(double B) { double tx = x,ty = y; x= tx*cos(B) - ty*sin(B); y= tx*sin(B) + ty*cos(B); } }; double AREA(Point a, double r1, Point b, double r2) { double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y)); if (d >= r1+r2) return 0; if (r1>r2) { double tmp = r1; r1 = r2; r2 = tmp; } if(r2 - r1 >= d) return pi*r1*r1; double ang1=acos((r1*r1+d*d-r2*r2)/(2*r1*d)); double ang2=acos((r2*r2+d*d-r1*r1)/(2*r2*d)); return ang1*r1*r1 + ang2*r2*r2 - r1*d*sin(ang1); } int main() { int T,cas=1; scanf("%d",&T); while(T--) { double r1,r2; Point a,b; scanf("%lf%lf%lf%lf%lf%lf",&r1,&r2,&a.x,&a.y,&b.x,&b.y); printf("Case #%d: %.6f\n",cas++,AREA(a,r2,b,r2)-AREA(a,r1,b,r2)-AREA(a,r2,b,r1)+AREA(a,r1,b,r1)); } return 0; }





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步