Codeforces Round #374 (Div. 2) D. Maxim and Array 线段树+贪心
Recently Maxim has found an array of n integers, needed by no one. He immediately come up with idea of changing it: he invented positive integer x and decided to add or subtract it from arbitrary array elements. Formally, by applying single operation Maxim chooses integer i (1 ≤ i ≤ n) and replaces the i-th element of array ai either with ai + x or with ai - x. Please note that the operation may be applied more than once to the same position.
Maxim is a curious minimalis, thus he wants to know what is the minimum value that the product of all array elements (i.e. 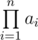 ) can reach, if Maxim would apply no more than k operations to it. Please help him in that.
) can reach, if Maxim would apply no more than k operations to it. Please help him in that.
The first line of the input contains three integers n, k and x (1 ≤ n, k ≤ 200 000, 1 ≤ x ≤ 109) — the number of elements in the array, the maximum number of operations and the number invented by Maxim, respectively.
The second line contains n integers a1, a2, ..., an (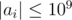 ) — the elements of the array found by Maxim.
) — the elements of the array found by Maxim.
Print n integers b1, b2, ..., bn in the only line — the array elements after applying no more than k operations to the array. In particular, 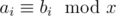 should stay true for every 1 ≤ i ≤ n, but the product of all array elements should be minimum possible.
should stay true for every 1 ≤ i ≤ n, but the product of all array elements should be minimum possible.
If there are multiple answers, print any of them.
5 3 1
5 4 3 5 2
5 4 3 5 -1
5 3 1
5 4 3 5 5
5 4 0 5 5
5 3 1
5 4 4 5 5
5 1 4 5 5
3 2 7
5 4 2
5 11 -5
题意:n个数,可以修改k次,每次可以+x或者-x,使得成绩最小;
思路:每次寻找绝对值最小的那个数,判断负数的个数,进行+x或者-x;
ps:优先队列也可做;
#include<bits/stdc++.h> using namespace std; #define ll long long #define pi (4*atan(1.0)) const int N=2e5+10,M=4e6+10,inf=1e9+10,mod=1e9+7; const ll INF=1e18+10; struct is { ll num; int pos; }tree[N<<2]; ll ans[N]; void pushup(int pos) { tree[pos].num=min(tree[pos<<1].num,tree[pos<<1|1].num); } void buildtree(int l,int r,int pos) { if(l==r) { tree[pos].num=abs(ans[l]); tree[pos].pos=l; return; } int mid=(l+r)>>1; buildtree(l,mid,pos<<1); buildtree(mid+1,r,pos<<1|1); pushup(pos); } void update(int p,ll c,int l,int r,int pos) { if(p==r&&p==l) { tree[pos].num=abs(c); return; } int mid=(l+r)>>1; if(p<=mid) update(p,c,l,mid,pos<<1); else update(p,c,mid+1,r,pos<<1|1); pushup(pos); } int query(ll x,int l,int r,int pos) { if(l==r&&tree[pos].num==x) return tree[pos].pos; int mid=(l+r)>>1; if(tree[pos<<1].num==x) return query(x,l,mid,pos<<1); else return query(x,mid+1,r,pos<<1|1); } int main() { int n,m,k; int flag=0; scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) { scanf("%lld",&ans[i]); if(ans[i]<0)flag++; } buildtree(1,n,1); while(m--) { ll x=tree[1].num; int pos=query(x,1,n,1); if(flag&1) { if(ans[pos]>=0) ans[pos]+=k; else ans[pos]-=k; update(pos,ans[pos],1,n,1); } else { if(ans[pos]>=0) { ans[pos]=ans[pos]-k; if(ans[pos]<0) flag++; } else { ans[pos]=ans[pos]+k; if(ans[pos]>=0) flag--; } update(pos,ans[pos],1,n,1); } } for(int i=1;i<=n;i++) printf("%lld ",ans[i]); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号