逆元的各种求解方式

若ax≡1 mod f, 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。

当a与f互素时，a关于模f的乘法逆元有唯一解。如果不互素，则无解。如果f为素数，则从1到f-1的任意数都与f互素，即在1到f-1之间都恰好有一个关于模f的乘法逆元。

（不会证明，想通了补）

首先a与f要互素，否则无逆元

1.扩展欧几里德：扩展欧几里德算法是用来在已知a, b求解一组x，y，使它们满足贝祖等式： ax+by = gcd(a, b) =d（解一定存在，根据数论中的相关定理）

　　　　　　　　扩展欧几里德的证明和代码http://www.cnblogs.com/jhz033/p/5330252.html

　　　　　　　　ax≡1 mod f；相当于ax+fy==1，因为gcd（a，f）==1；

　　　　　　　　x解出来就是逆元

2.费马小定理：假如a是整数，p是质数，且a,p互质(即两者只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。

　　　　　　   如果f为素数。可以根据费马小定理得到逆元为。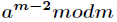

     　　　　　推导过程如下

                            

3.公式如下

          

现在我们来证明它，已知，证明步骤如下

          

上面部分取自http://blog.csdn.net/acdreamers/article/details/8220787

 

逆元打表，根据模的那个数如果是素数m，可以o(n)直接打表所有的对m的逆元，不用每次都log级别求逆元；

typedef  long long ll;  
const int N = 1e5 + 5;  
int inv[N];  
   
void inverse(int n, int p) {  
    inv[1] = 1;  
    for (int i=2; i<=n; ++i) {  
        inv[i] = (ll) (p - p / i) * inv[p%i] % p;  
    }  
}