python对肌电信号进行简单的手势识别

采集前臂四块不同肌肉的表面肌电信号

#加载相关模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
#读取数据
data1=pd.read_excel('wq20.xlsx',sheetname=1)
data2=pd.read_excel('zs20.xlsx',sheetname=1)
data3=pd.read_excel('n20.xlsx',sheetname=1)
data4=pd.read_excel('w20.xlsx',sheetname=1)
data1.columns=['ch1','ch2','ch3','ch4']
data2.columns=['ch1','ch2','ch3','ch4']
data3.columns=['ch1','ch2','ch3','ch4']
data4.columns=['ch1','ch2','ch3','ch4']
names=locals()
for i in range(1,5):
    plt.figure()
    plt.plot(names['data%s'%i])

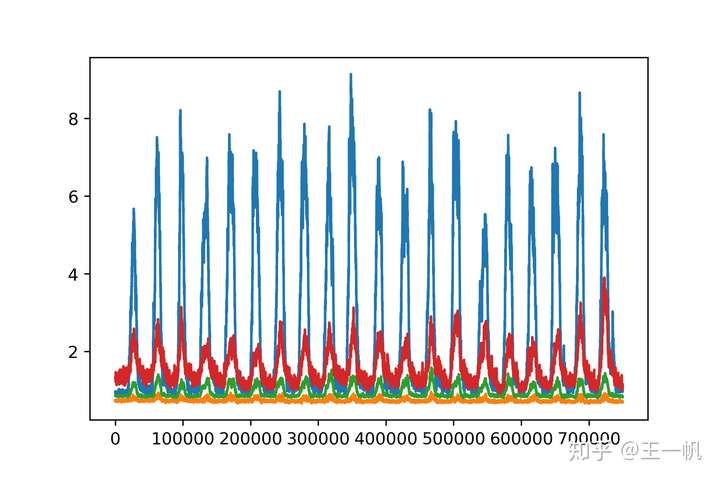
握拳

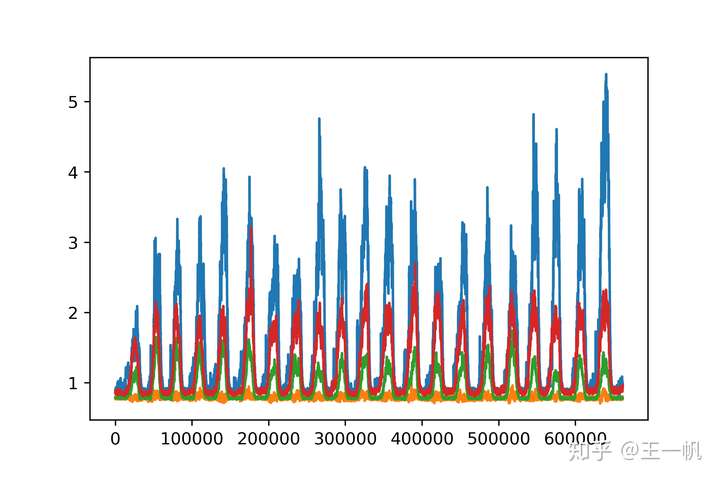
张手

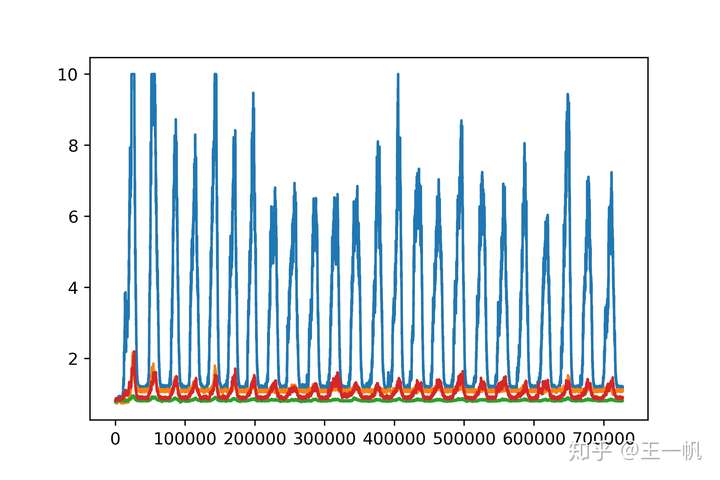
手腕内翻

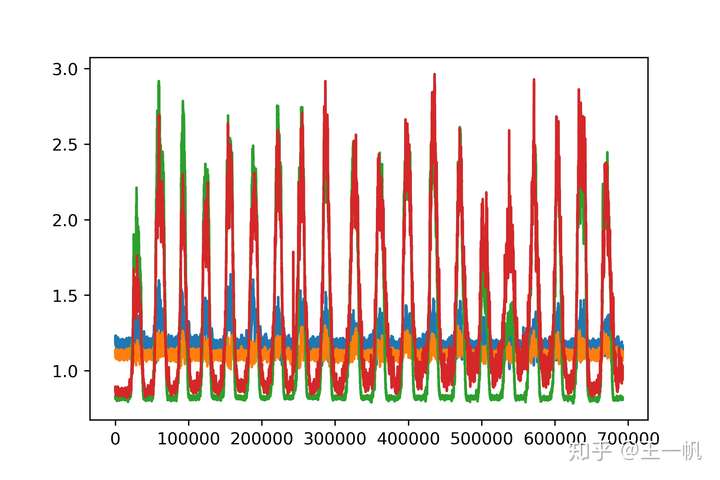
手腕外翻

将四通道的肌肉电信号汇总求其绝对值平均值，利用移动窗口法，取若干连续时间序列对应的信号强度求局域平均，若其后若干点的均值都超过一定阈值，则视为一个动作开始，反之若其后若干点的局域均值都小于阈值，则视为一个动作结束

 

def get_mean_semg(data):
    mean_semg=[]
    for i in range(len(data)-1):
        mean_semg.append((data.ch1[i]+data.ch2[i]+data.ch3[i]+data.ch4[i])/4)
    return mean_semg


for i in range(1,5):
    names['mean_semg_%s'%i]=get_mean_semg(names['data%s'%i])
    plt.figure()
    plt.plot(names['mean_semg_%s'%i])
    plt.ylim(0,5)
    plt.savefig('a%s'%i,dpi=400)

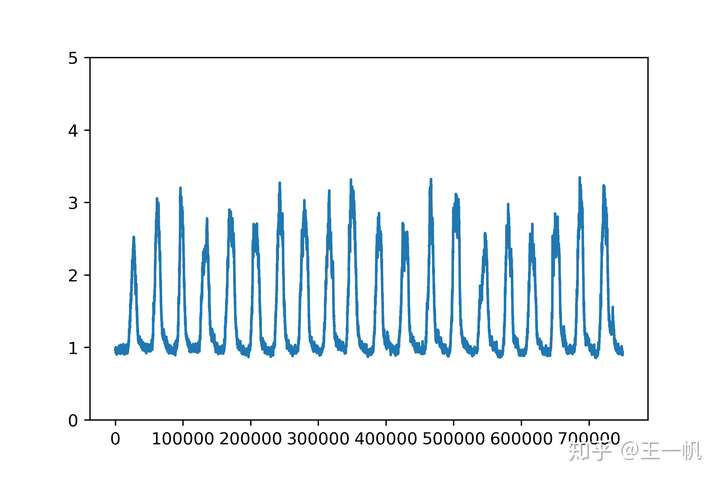
握拳

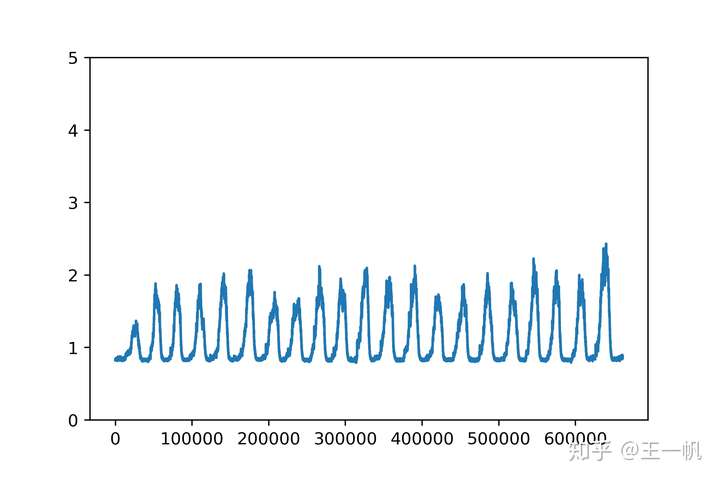
张手

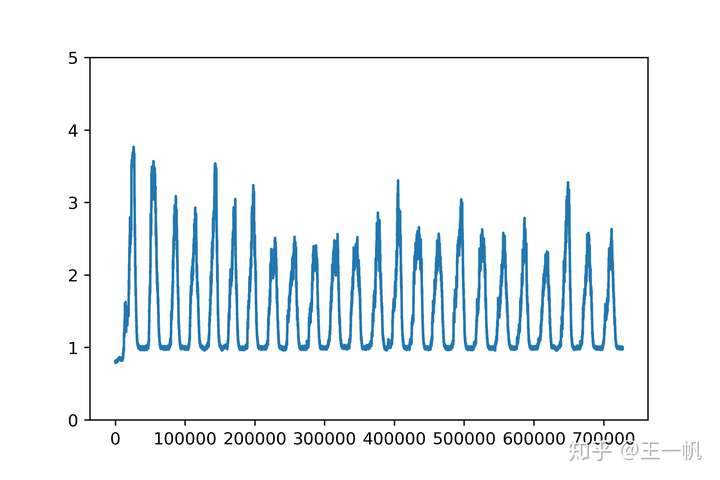
内翻

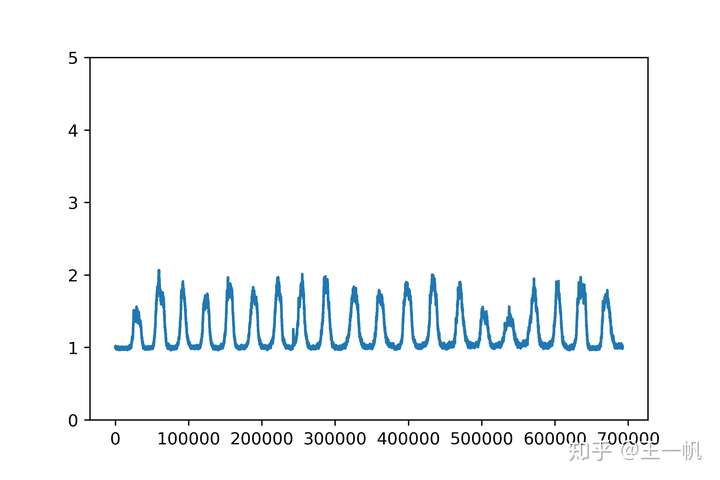
外翻

 

def get_move_window(mean_semg):
    mean_semg_arr=np.array(mean_semg)
    return pd.rolling_mean(mean_semg_arr,window=800)
    
def get_break(data,i,thre,windowlenth):
    for i in range(i,i+windowlenth):
        if data[i]<thre:
            return 0
    return 1

for i in range(1,5):
    names['move_averge_%s'%i]=get_move_window(names['mean_semg_%s'%i])
    names['sta_%s'%i]=[]
    names['end_%s'%i]=[]
    thre=1.1
    windowlenth=800
    for j in range(len(names['move_averge_%s'%i])-1):
        if get_break(names['move_averge_%s'%i],j,thre,windowlenth)==0 and get_break(names['move_averge_%s'%i],j+1,thre,windowlenth)==1:
            names['sta_%s'%i].append(j)
        if get_break(names['move_averge_%s'%i],j,thre,windowlenth)==1 and get_break(names['move_averge_%s'%i],j+1,thre,windowlenth)==0:
            names['end_%s'%i].append(j)

 

获取平均值起始点，并将对应时间点作用于原始信号上，对四通道信号进行行动段提取，并将长度较小的部分过滤，视为噪音

 

for i in range(1,5):
    names['period_%s'%i]=[]
    names['sta_filt_%s'%i]=[]
    names['end_filt_%s'%i]=[]
    for j in range(len(names['sta_%s'%i])):
        names['period_%s'%i].append(names['end_%s'%i][j]-names['sta_%s'%i][j])
    for k in range(len(names['period_%s'%i])):
        if names['period_%s'%i][k]>5000:
            names['sta_filt_%s'%i].append(names['sta_%s'%i][k])
            names['end_filt_%s'%i].append(names['end_%s'%i][k])
for i in range(1,len(sta_filt_1)+1):
    names['data1_cut%s'%i]=data1[sta_filt_1[i-1]:end_filt_1[i-1]]
for i in range(1,len(sta_filt_2)+1):
    names['data2_cut%s'%i]=data2[sta_filt_2[i-1]:end_filt_2[i-1]]
for i in range(1,len(sta_filt_3)+1):
    names['data3_cut%s'%i]=data3[sta_filt_3[i-1]:end_filt_3[i-1]]
for i in range(1,len(sta_filt_4)+1):
    names['data4_cut%s'%i]=data4[sta_filt_4[i-1]:end_filt_4[i-1]]
    
   

plt.figure(figsize=(50,3))
for i in range(1,21):
    plt.subplot2grid((1,20),(0,i-1),colspan=1).plot(names['data1_cut%s'%i])
    plt.ylim(0,10)
    plt.title('fist')
plt.figure(figsize=(50,3))
for i in range(1,22):
    plt.subplot2grid((1,21),(0,i-1),colspan=1).plot(names['data2_cut%s'%i])
    plt.ylim(0,10)
    plt.title('open')
plt.figure(figsize=(50,3))
for i in range(1,25):
    plt.subplot2grid((1,24),(0,i-1),colspan=1).plot(names['data3_cut%s'%i])
    plt.ylim(0,10)
    plt.title('toright')
plt.figure(figsize=(50,3))
for i in range(1,21):
    plt.subplot2grid((1,20),(0,i-1),colspan=1).plot(names['data4_cut%s'%i])
    plt.ylim(0,10)
    plt.title('toleft')

握拳

张手

内弯

外翻

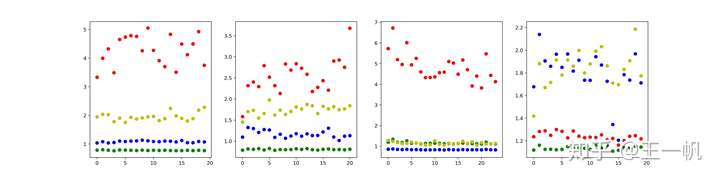
对各通道行动段求区间的平均值MAV，可以看出对于不同的动作，MAV值区别明显，可以作为特征向量对信号进行特征提取

 

mav_fist=pd.DataFrame(columns=['ch1','ch2','ch3','ch4'],index=[np.arange(20)])
for i in range(1,21):
    mav_fist.loc[i-1,'ch1']=names['data1_cut%s'%i].ch1.mean()
    mav_fist.loc[i-1,'ch2']=names['data1_cut%s'%i].ch2.mean()
    mav_fist.loc[i-1,'ch3']=names['data1_cut%s'%i].ch3.mean()
    mav_fist.loc[i-1,'ch4']=names['data1_cut%s'%i].ch4.mean()
mav_open=pd.DataFrame(columns=['ch1','ch2','ch3','ch4'],index=[np.arange(21)])
for i in range(1,22):
    mav_open.loc[i-1,'ch1']=names['data2_cut%s'%i].ch1.mean()
    mav_open.loc[i-1,'ch2']=names['data2_cut%s'%i].ch2.mean()
    mav_open.loc[i-1,'ch3']=names['data2_cut%s'%i].ch3.mean()
    mav_open.loc[i-1,'ch4']=names['data2_cut%s'%i].ch4.mean()
mav_toright=pd.DataFrame(columns=['ch1','ch2','ch3','ch4'],index=[np.arange(24)])
for i in range(1,25):
    mav_toright.loc[i-1,'ch1']=names['data3_cut%s'%i].ch1.mean()
    mav_toright.loc[i-1,'ch2']=names['data3_cut%s'%i].ch2.mean()
    mav_toright.loc[i-1,'ch3']=names['data3_cut%s'%i].ch3.mean()
    mav_toright.loc[i-1,'ch4']=names['data3_cut%s'%i].ch4.mean()
mav_toleft=pd.DataFrame(columns=['ch1','ch2','ch3','ch4'],index=[np.arange(20)])
for i in range(1,21):
    mav_toleft.loc[i-1,'ch1']=names['data4_cut%s'%i].ch1.mean()
    mav_toleft.loc[i-1,'ch2']=names['data4_cut%s'%i].ch2.mean()
    mav_toleft.loc[i-1,'ch3']=names['data4_cut%s'%i].ch3.mean()
    mav_toleft.loc[i-1,'ch4']=names['data4_cut%s'%i].ch4.mean()

 

 

plt.figure(figsize=(20,5))
mav_fist_ax=plt.subplot2grid((1,4),(0,0),colspan=1)
mav_fist_ax.scatter(x=np.arange(20),y=mav_fist.ch1,c='r')
mav_fist_ax.scatter(x=np.arange(20),y=mav_fist.ch2,c='g')
mav_fist_ax.scatter(x=np.arange(20),y=mav_fist.ch3,c='b')
mav_fist_ax.scatter(x=np.arange(20),y=mav_fist.ch4,c='y')
mav_open_ax=plt.subplot2grid((1,4),(0,1),colspan=1)
mav_open_ax.scatter(x=np.arange(21),y=mav_open.ch1,c='r')
mav_open_ax.scatter(x=np.arange(21),y=mav_open.ch2,c='g')
mav_open_ax.scatter(x=np.arange(21),y=mav_open.ch3,c='b')
mav_open_ax.scatter(x=np.arange(21),y=mav_open.ch4,c='y')
mav_toright_ax=plt.subplot2grid((1,4),(0,2),colspan=1)
mav_toright_ax.scatter(x=np.arange(24),y=mav_toright.ch1,c='r')
mav_toright_ax.scatter(x=np.arange(24),y=mav_toright.ch2,c='g')
mav_toright_ax.scatter(x=np.arange(24),y=mav_toright.ch3,c='b')
mav_toright_ax.scatter(x=np.arange(24),y=mav_toright.ch4,c='y')
mav_toleft_ax=plt.subplot2grid((1,4),(0,3),colspan=1)
mav_toleft_ax.scatter(x=np.arange(20),y=mav_toleft.ch1,c='r')
mav_toleft_ax.scatter(x=np.arange(20),y=mav_toleft.ch2,c='g')
mav_toleft_ax.scatter(x=np.arange(20),y=mav_toleft.ch3,c='b')
mav_toleft_ax.scatter(x=np.arange(20),y=mav_toleft.ch4,c='y')

 

mav_fist['action']=0
mav_open['action']=1
mav_toright['action']=2
mav_toleft['action']=3
sumup=mav_fist.append([mav_open,mav_toright,mav_toleft],ignore_index=True)
y=sumup.action

x=sumup.drop(['action'],axis=1)
from sklearn.model_selection import train_test_split

import xgboost as xgb
train_x,test_x,train_y,test_y=train_test_split(x.as_matrix(),y.as_matrix(),test_size=0.2)
xg_train=xgb.DMatrix(train_x,label=train_y)
xg_test=xgb.DMatrix(test_x,label=test_y)
param = {}

param['objective'] ='multi:softmax'

param['eta']=0.1
param['max_depth']=6
param['silent']=1
param['nthread']=4
param['num_class']=4
watchlist = [(xg_train, 'train'), (xg_test, 'test')]
num_round=5
bst = xgb.train(param, xg_train, num_round, watchlist)
pred = bst.predict(xg_test)

对四个不同的手势进行数字命名，通过xgboost进行训练分析，16个测试样的预测结果正确率为100%

更多Python视频、源码、资料加群683380553免费获取

转载至：https://zhuanlan.zhihu.com/p/41073513