数模-微分方程(SIR模型)
SIR模型
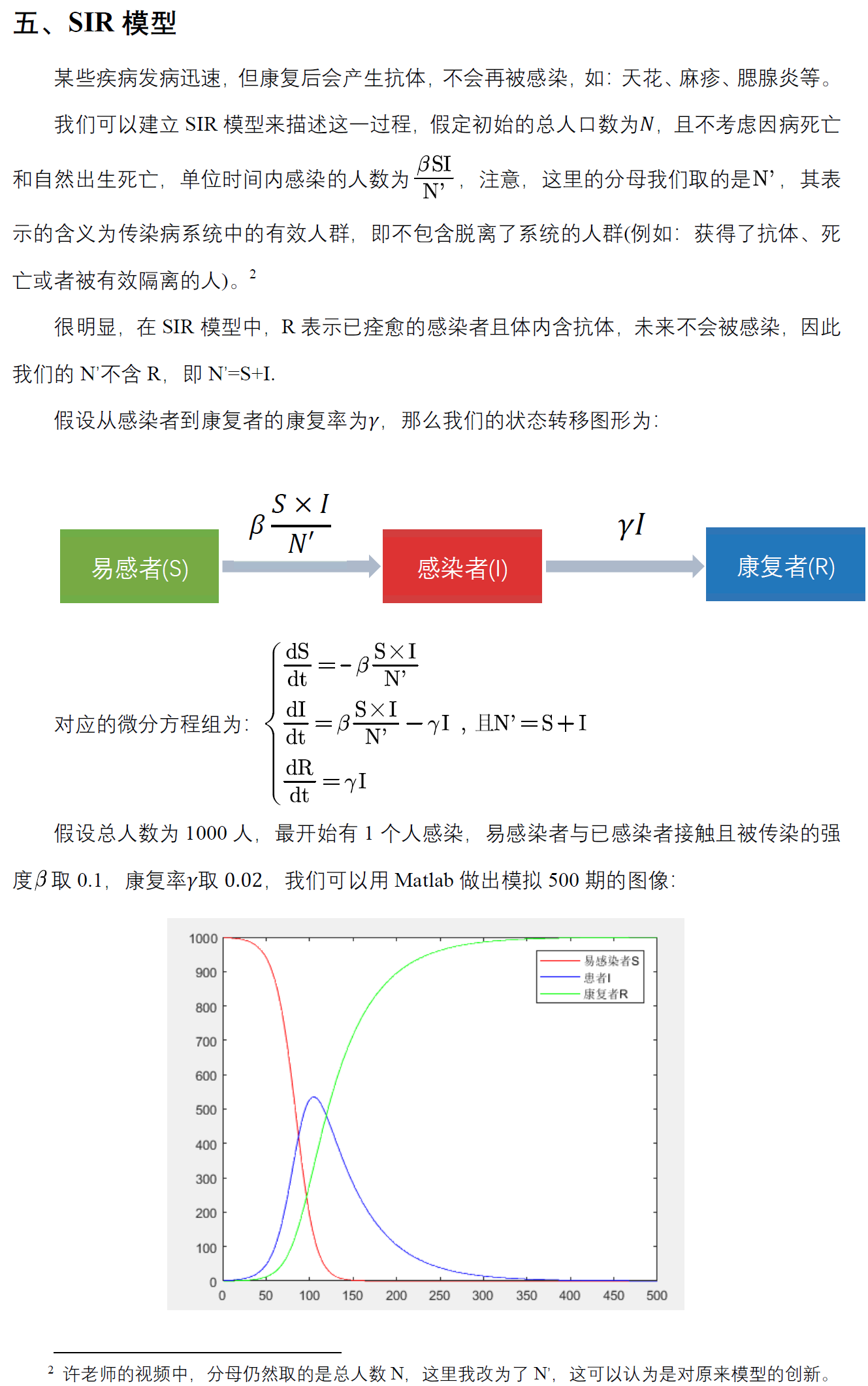
代码
fun1.m
function dx=fun1(t,x) % 大家可以修改里面的参数,来看结果的变化
beta = 0.1; % 易感染者与已感染者接触且被传染的强度
gamma = 0.02; % 康复率
dx = zeros(3,1); % x(1)表示S x(2)表示I x(3)表示R
C = x(1)+x(2); % 传染病系统中的有效人群,也就是课件中的N' = S+I
dx(1) = - beta*x(1)*x(2)/C;
dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
dx(3) = gamma*x(2);
end
code.m
%% 最简单的SIR模型
clc;clear
N = 1000; % 总人数
i0 = 1; % 初始时刻患者(已感染者)的人数
[t,x]=ode45('fun1',[1:500],[N-i0 i0 0]); % 记得给康复者R一个初始值
x = round(x); % 对x进行四舍五入(人数为整数)
figure(1)
% x的第一列是易感染者S的数量,x的第二列是患者I的数量,x的第三列是康复者R的数量
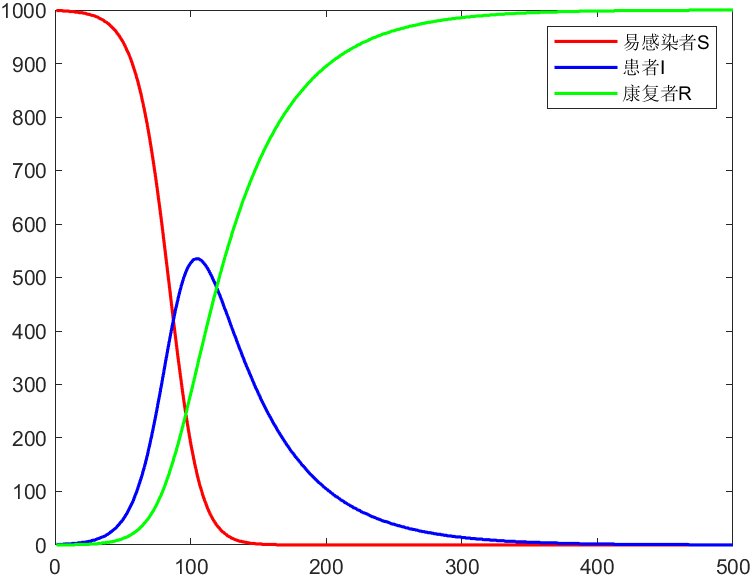
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-','Linewidth',1.5)
legend('易感染者S','患者I','康复者R')
结果
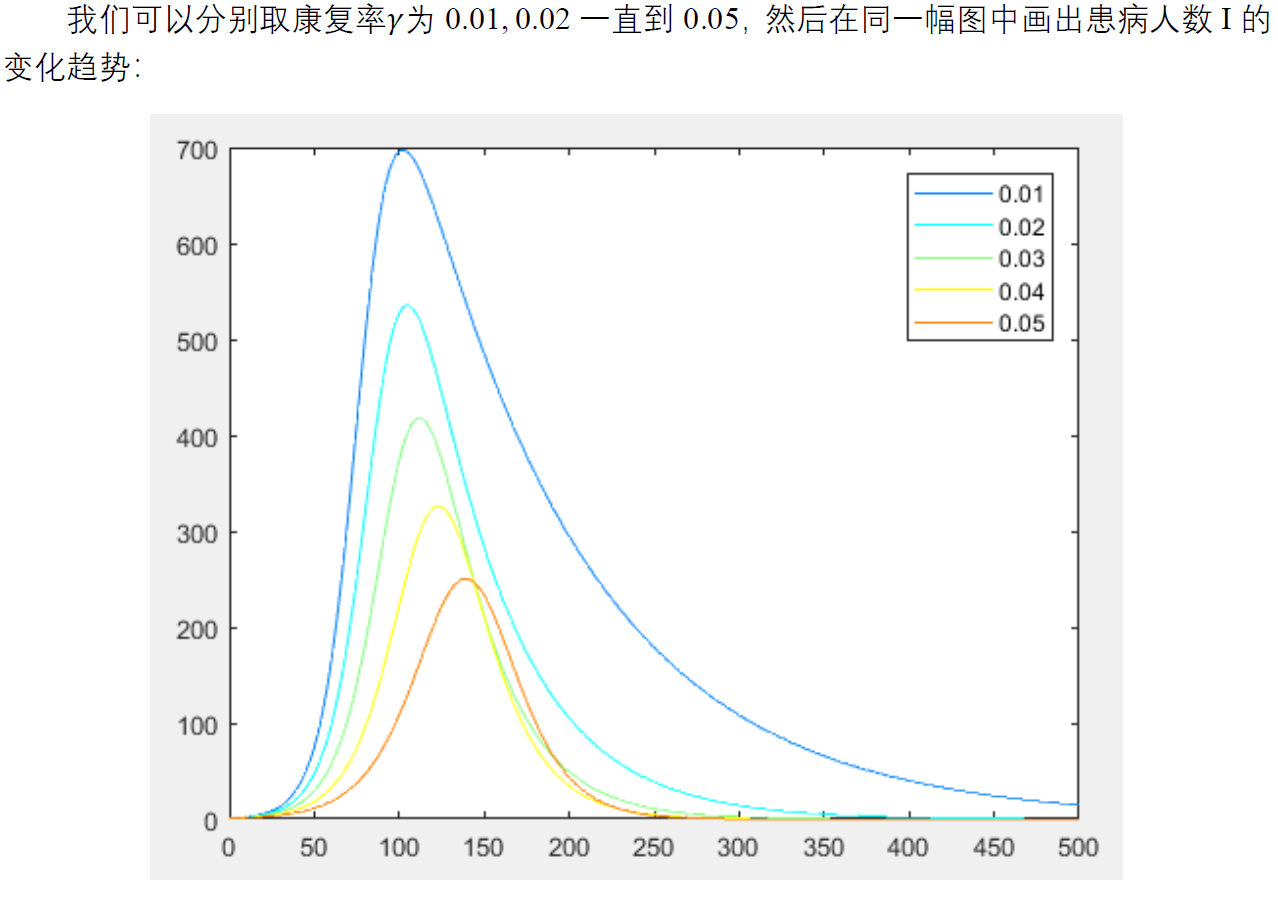
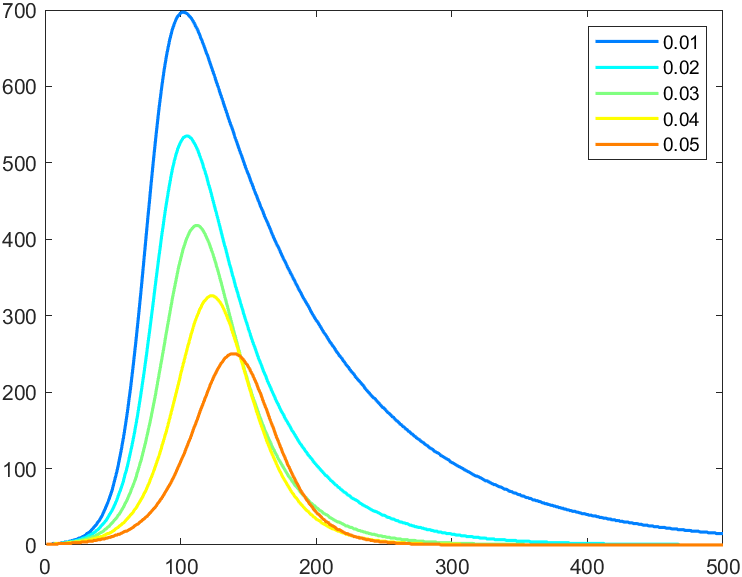
分别取康复率为0.01,0.02一直到0.05,把患病人数I的结果放到一个图形上(相对于上面的模型)
代码
fun2.m
function dx=fun2(t,x) % 大家可以修改里面的参数,来看结果的变化
global GAMMA % 定义康复率为全局变量
beta = 0.1; % 易感染者与已感染者接触且被传染的强度
dx = zeros(3,1); % x(1)表示S x(2)表示I x(3)表示R
C = x(1)+x(2); % 传染病系统中的有效人群,也就是课件中的N' = S+I
dx(1) = - beta*x(1)*x(2)/C;
dx(2) = beta*x(1)*x(2)/C - GAMMA*x(2);
dx(3) = GAMMA*x(2);
end
code.m
%% 分别取康复率为0.01,0.02一直到0.05,把患病人数I的结果放到一个图形上
clc;clear
global GAMMA % 定义康复率为全局变量(我习惯用大写字母来定义)
N = 1000; % 总人数
i0 = 1; % 初始时刻患者(已感染者)的人数
% https://ww2.mathworks.cn/help/matlab/ref/colormap.html
c = jet(5); % jet是matlab自带的颜色图数组,等会画图我们要用不同颜色区分
% 每行一个0-1之间三元素 RGB 向量。第一列红色强度。第二列绿色强度。第三列蓝色强度。
for i = 1:5
GAMMA = 0.01*i; % 在循环中来改变康复率GAMMA的值
[t,x]=ode45('fun2',[1:500],[N-i0 i0 0]); % 记得给康复者R一个初始值
x = round(x); % 对x进行四舍五入(人数为整数)
% x的第一列是易感染者S的数量,x的第二列是患者I的数量,x的第三列是康复者R的数量
figure(2)
% 这里我们就只绘制患病人数I的图形了
plot(t, x(:,2), '-', 'color', c(i,:),'DisplayName',num2str(GAMMA),'Linewidth',1.5)
% 'color' 后面的c(i,:)是前面生成的一个RGB向量,可以用来指定这个曲线的颜色
% 'DisplayName' 后面需要加上当前图例对应的文本
hold on
end
legend show % 要加上这句话,否则图例不会显示
% 等价于直接使用命令: legend('0.01','0.02','0.03','0.04','0.05')
结果
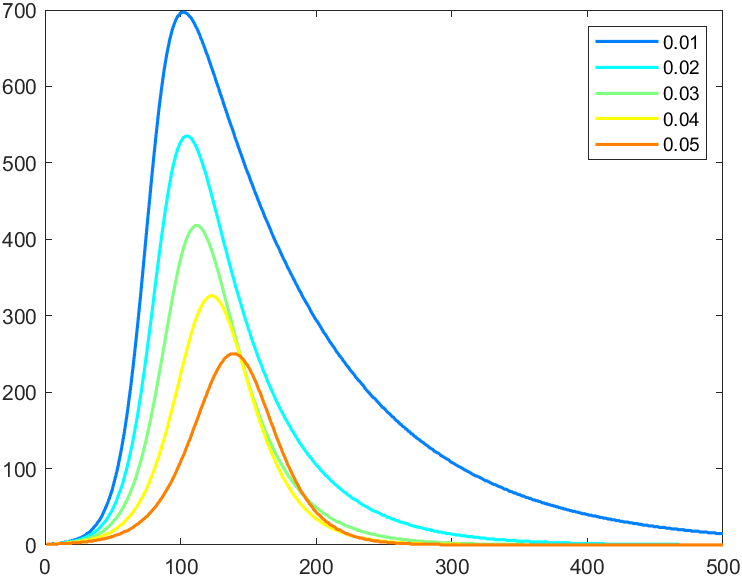
不定义全局变量,我们可以用另外一种方法(这种方法的通用性更强)
由于我们参数多加了一个GAMMA,所以我们要改为函数句柄的方式
代码
newfun2.m
% % 不定义全局变量的写法
function dx=newfun2(t,x,GAMMA) % 把GAMMA当成参数传入进来
beta = 0.1; % 易感染者与已感染者接触且被传染的强度
dx = zeros(3,1); % x(1)表示S x(2)表示I x(3)表示R
C = x(1)+x(2); % 传染病系统中的有效人群,也就是课件中的N' = S+I
dx(1) = - beta*x(1)*x(2)/C;
dx(2) = beta*x(1)*x(2)/C - GAMMA*x(2);
dx(3) = GAMMA*x(2);
end
code.m
% % 不定义全局变量,我们可以用另外一种方法(这种方法的通用性更强)
clc;clear
N = 1000; % 总人数
i0 = 1; % 初始时刻患者(已感染者)的人数
c = jet(5);
for i = 1:5
GAMMA = 0.01*i; % 在循环中来改变康复率GAMMA的值
[t,x]=ode45(@(t,x) newfun2(t,x,GAMMA),[1:500],[N-i0 i0 0]);
x = round(x); % 对x进行四舍五入(人数为整数)
% x的第一列是易感染者S的数量,x的第二列是患者I的数量,x的第三列是康复者R的数量
figure(2)
% 这里我们就只绘制患病人数I的图形了
plot(t, x(:,2), '-', 'color', c(i,:),'DisplayName',num2str(GAMMA),'Linewidth',1.5)
hold on
end
legend show % 要加上这句话,否则图例不会显示
结果
SIR模型的扩展1
代码
fun3.m
function dx=fun3(t,x) % 大家可以修改里面的参数,来看结果的变化
beta = 0.1; % 易感染者与已感染者接触且被传染的强度
gamma = 0.01; % 康复率
if t > 100
gamma = gamma * 10; % 第100期后研发了疫苗,使得康复率增加为原来的10倍
end
dx = zeros(3,1); % x(1)表示S x(2)表示I x(3)表示R
C = x(1)+x(2); % 传染病系统中的有效人群,也就是课件中的N' = S+I
dx(1) = - beta*x(1)*x(2)/C;
dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
dx(3) = gamma*x(2);
end
code.m
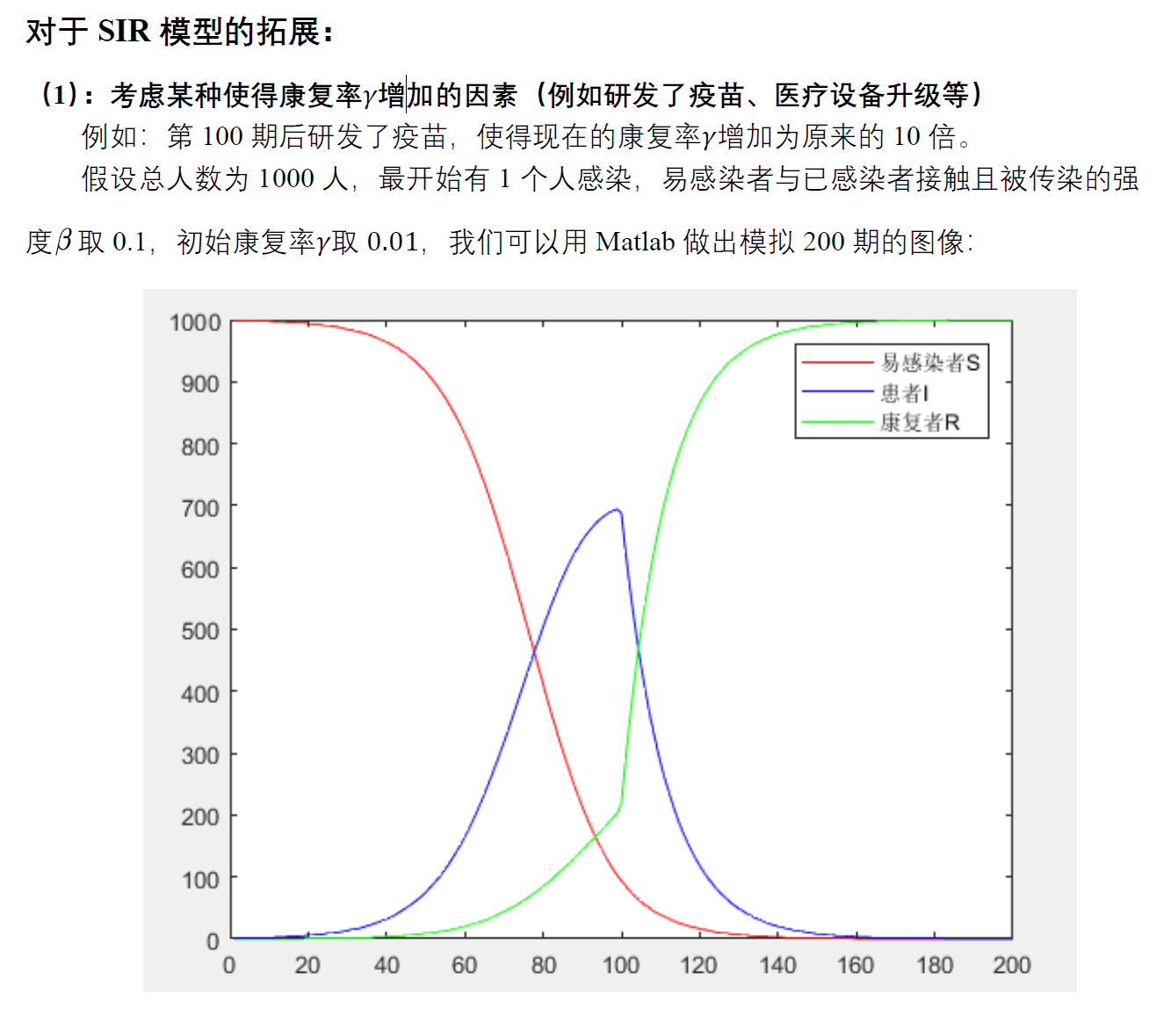
%% 考虑某种使得康复率gamma增加的因素(例如研发了疫苗、医疗设备升级等)
% 第100期后研发了疫苗,使得康复率增加为原来的10倍
clc;clear
N = 1000; % 总人数
i0 = 1; % 初始时刻患者(已感染者)的人数
[t,x]=ode45('fun3',[1:200],[N-i0 i0 0]); % 记得给康复者R一个初始值
x = round(x); % 对x进行四舍五入(人数为整数)
figure(3)
% x的第一列是易感染者S的数量,x的第二列是患者I的数量,x的第三列是康复者R的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-','Linewidth',1.5)
legend('易感染者S','患者I','康复者R')
结果
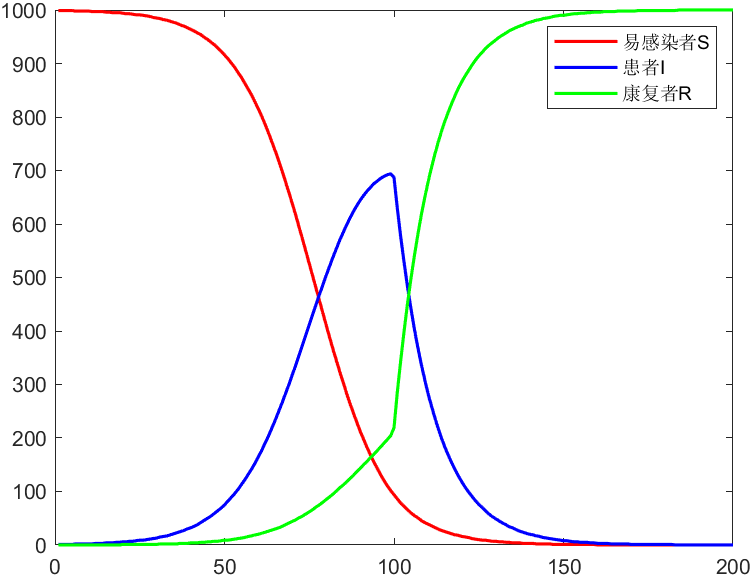
SIR模型的扩展2
代码
fun4.m
function dx=fun4(t,x) % 大家可以修改里面的参数,来看结果的变化
beta = 0.1; % 易感染者与已感染者接触且被传染的强度
gamma = 0.02; % 康复率
d = 0.005; % 因病的死亡率
dx = zeros(4,1); % x(1)表示S x(2)表示I x(3)表示R x(4)表示ID
C = x(1)+x(2); % 传染病系统中的有效人群,也就是课件中的N' = S+I
dx(1) = - beta*x(1)*x(2)/C;
dx(2) = beta*x(1)*x(2)/C - gamma*x(2) -d*x(2);
dx(3) = gamma*x(2);
dx(4) = d*x(2);
end
code.m
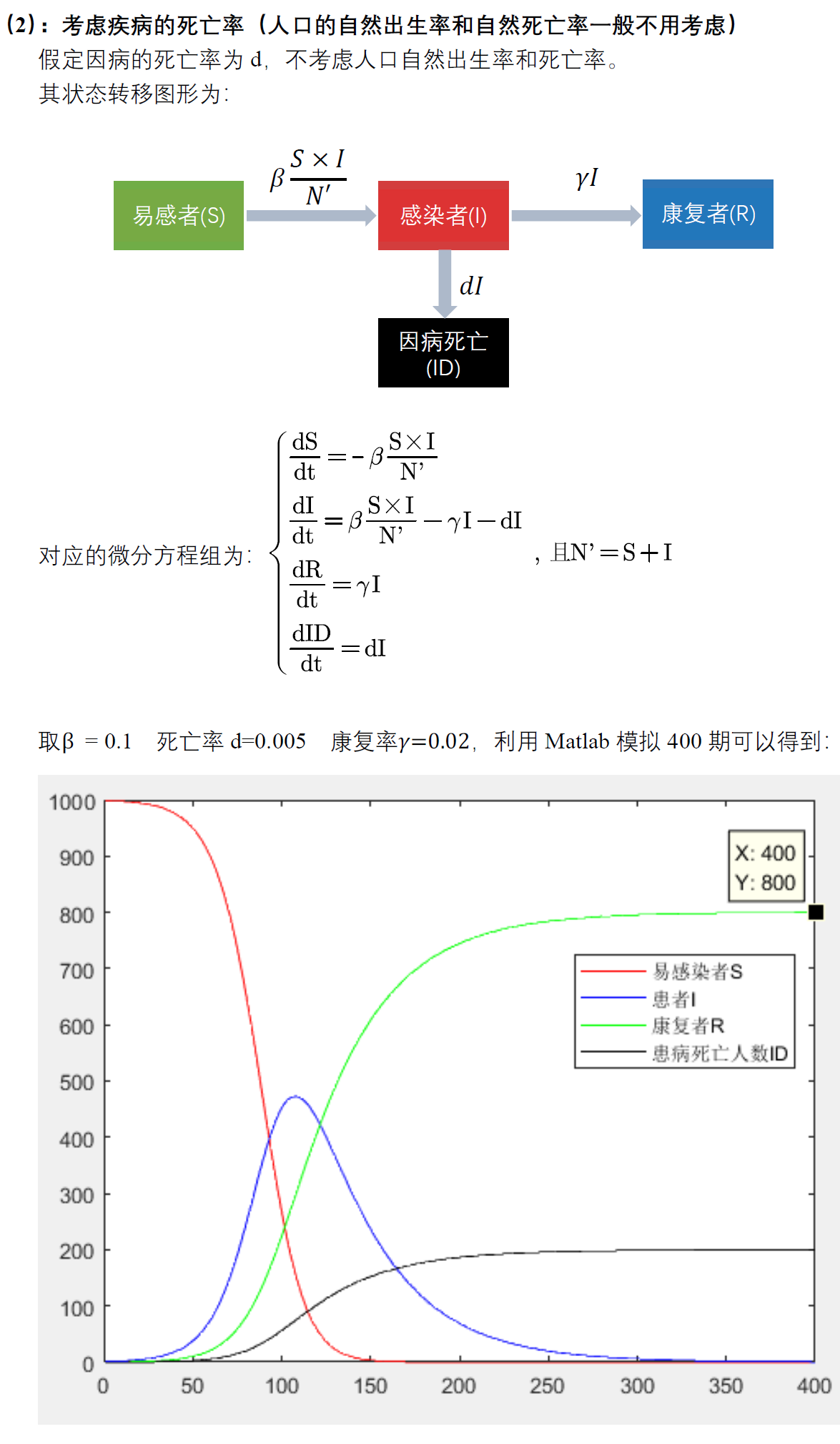
%% 考虑疾病的死亡率的SIR模型
clc;clear
N = 1000; % 总人数
i0 = 1; % 初始时刻患者(已感染者)的人数
[t,x]=ode45('fun4',[1:400],[N-i0 i0 0 0]); % 记得给患病死亡人数ID一个初始值
x = round(x); % 对x进行四舍五入(人数为整数)
figure(4)
% x的第一列是易感染者S的数量,x的第二列是患者I的数量
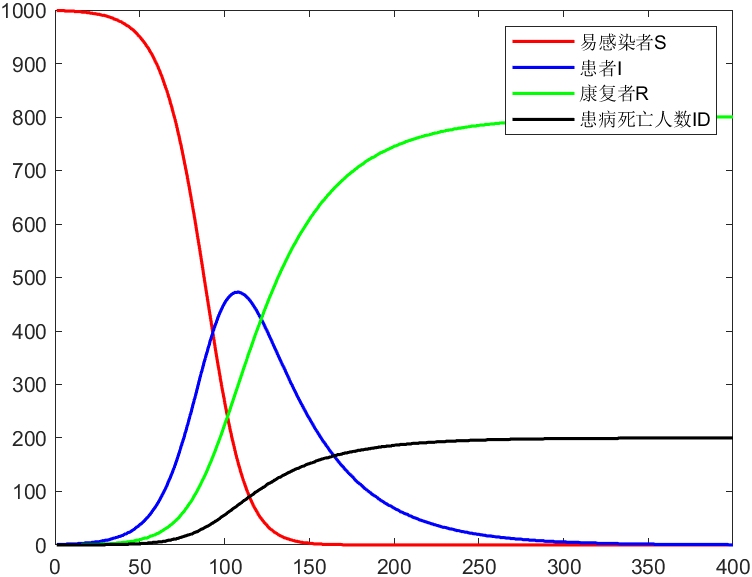
% x的第三列是康复者R的数量, x的第四列是患病死亡人数ID的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-',t,x(:,4),'k-','Linewidth',1.5)
legend('易感染者S','患者I','康复者R','患病死亡人数ID')
结果
转载请注明出处,欢迎讨论和交流!

